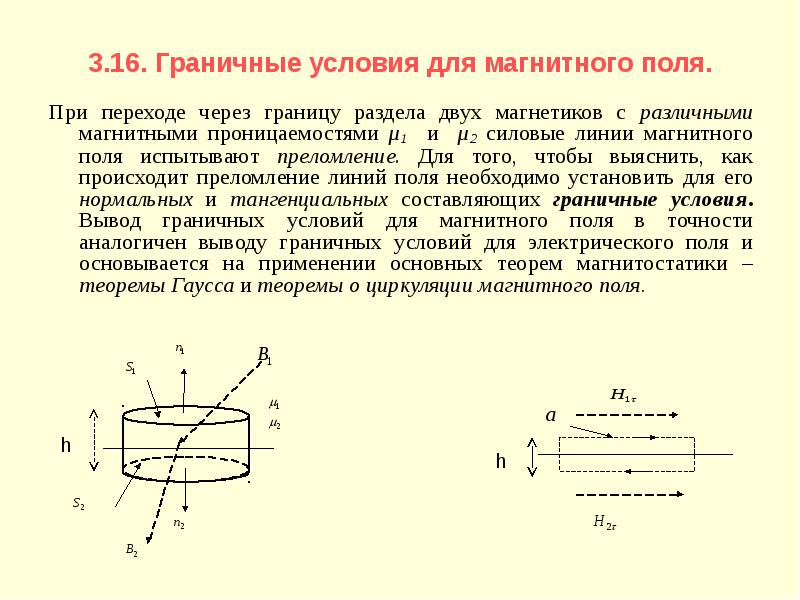
Описание слайда:
Ферримагнетики (ферриты) – вещества, в которых магнитные моменты атомов кристаллической решетки образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг другу. Имея меньшую величину магнитной восприимчивости по сравнению с ферромагнетиками, в остальном ферримагнетики характеризуются теми же признаками, что и ферромагнетики. Типичными ферритами являются соединения оксидов железа с оксидами других металлов - шпинели (MnFe2O4), гранаты Gd3Fe5O12), гексаферриты (PbFe12O19). Другую группу ферритов образуют двойные фториды типа RbNiF3, а также соединения типа RFe2 (R – редкоземельный металл).
Ферримагнетики (ферриты) – вещества, в которых магнитные моменты атомов кристаллической решетки образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг другу. Имея меньшую величину магнитной восприимчивости по сравнению с ферромагнетиками, в остальном ферримагнетики характеризуются теми же признаками, что и ферромагнетики. Типичными ферритами являются соединения оксидов железа с оксидами других металлов - шпинели (MnFe2O4), гранаты Gd3Fe5O12), гексаферриты (PbFe12O19). Другую группу ферритов образуют двойные фториды типа RbNiF3, а также соединения типа RFe2 (R – редкоземельный металл).
Антиферромагнетики – частный случай ферримагнетиков, в которых магнитные моменты подрешеток с противоположно направленными магнитными моментами полностью компенсируют друг друга (скомпенсированный ферримагнетик). Существование антиферромагнетиков было предсказано Л.Д.Ландау в 1933г. В настоящее время известен широкий спектр веществ, обладающих антиферромагнитными свойствами: редкоземельные элементы (Er, Dy, Ho), оксиды и дифториды некоторых металлов (FeO, MnO, CoF2, NiF2), соли угольной и серной кислот (MnCO3, NiSO4) и другие.
Сверхдиамагнетики (идеальные диамагнетики) – вещества, магнитная проницаемость μ которых равна нулю. Благодаря этой особенности для сверхдиамагнетиков имеет место эффект Мейсснера-Оксенфельда (Meissner W., 1882-1974; Ocksenfeld C.) – полное выталкивание магнитного поля из объема сверхдиамагнетика (магнитная индукция=0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии - низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики).