Содержание ▲
- Космология
Наука о возникновении
и развитии…
- 2 лекция
Космологические модели
Закон…
- Закон Хаббла (продолжение)
Интерпретируя сдвиг…
- Слайд №4
- Слайд №5
- Слайд №6
- Слайд №7
- Закон Хаббла
Итак, в случае линейной зависимости…
- 2 лекция
Космологические модели
Закон…
- Красное смещение
Сдвиг длины волны определяют…
- Красное смещение
Причины для изменения длины…
- Эффект Допплера
Длина волны изменяется из-за…
- Слайд №13
- Слайд №14
- Эффект Допплера
Точная формула:
v – модуль…
- Расширение пространства
Длина волны изменяется,…
- Расширение пространства
Интегральная формула:
a…
- Красное смещение
Так как красное смещение…
- Суть постоянной Хаббла
Размерность постоянной…
- Метагалактика
Отсюда следует, что у Вселенной…
- 2 лекция
Космологические модели
Закон…
- Космологические модели
Космологической моделью…
- Космологические модели
Основные предположения,…
- Ньютоновская космология
Рассмотрим «типичный»…
- Ньютоновская космология
Пусть в момент времени…
- Ньютоновская космология
Для определения…
- Ньютоновская космология
Закон сохранения…
- Ньютоновская космология
Запишем полную…
- Ньютоновская космология
Это уравнение вместе с…
- Ньютоновская космология
Качественно можно…
- Ньютоновская космология
Если k<0, то полная…
- Ньютоновская космология
Знак постоянной k и…
- Ньютоновская космология
Если…
- Ньютоновская космология
Решим уравнение эволюции…
-
Ньютоновская космология
…
-
Ньютоновская космология
…
- Ньютоновская космология
Классическая космология…
- 2 лекция
Космологические модели
Закон…
- Релятивистская космология
Согласно…
- История
В 1916 году А. Эйнштейн создает общую…
- История
В 1917 году А. Эйнштейн создает модель…
-
История
…
- История
В 1922 году А.А. Фридман и, независимо…
-
История
…
- 2 лекция
Космологические модели
Закон…
- Основные понятия
Основные понятия ньютоновской…
- Основные понятия
Основные понятия…
- Основные понятия ОТО
Локально-инерциальная…
- Основные понятия ОТО
Пространство-время Римана –…
- Основные понятия ОТО
Кривые 4-х мерные…
- Слайд №51
- Основные понятия ОТО
Согласно ОТО,…
- Уравнения Эйнштейна
Кривизну с распределением…
- Тензор энергии-импульса
Рассмотрим вид тензора…
- Тензор энергии-импульса
Тензор энергии-импульса…
- Тензор энергии-импульса
Тензор энергии-импульса…
- Тензор энергии-импульса
Открытый вид тензора…
- Уравнение состояния
Давление с плотностью…
- 2 лекция
Космологические модели
Закон…
- Фридмановские модели
Основные…
- Фридмановские модели
Основные…
- Фридмановские модели
Эти уравнения не…
- Фридмановские модели
Хотя уравнения…
- Фридмановские модели
Но так как уравнения…
- Эволюция Вселенной
Эволюция зависит от одного…
-
Эволюция Вселенной
…
- Эволюция Вселенной
Постоянная Хаббла – мера…
- 2 лекция
Космологические модели
Закон…
- Наша Вселенная
Мы рассмотрели общую схему…
- Наша Вселенная
Преобразуем уравнение Фридмана…
- Наша Вселенная
Во Вселенной одновременно есть…
- - член
Исторически первая модель вселенной…
- - член
Уравнения Эйнштейна:
Уравнения,…
- - член
Найдём эффективное уравнение состоя-ния…
- - член
Сравнивая с общим видом тензора энергии…
- - член
Действительно, из уравнения…
- Наша Вселенная
Итак, обычное вещество с 0…
- 2 лекция
Космологические модели
Закон…
- Модель эволюции Вселенной
Обобщим…
- Состояния вещества
Пыль:
Плотность энергии…
- Плотность энергии
Уравнение, описывающее…
-
Плотность энергии
…
- Масштабный фактор
Уравнение Фридмана описывает…
- Масштабный фактор
Если -1, то
Если = -1,…
- Постоянная Хаббла
Если a(t) – степенная функция,…
- Температура
Зависимость температуры излучения от…
-
Параметры вещества
…
- Выводы
Узнали главные экспериментальные факты…
-
Спасибо за внимание!
…
- Скачать
- Похожие презентации
Слайды и текст этой презентации
Слайд 1

Описание слайда:
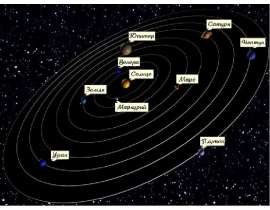
Космология
Наука о возникновении
и развитии Вселенной
Слайд 2

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 3

Описание слайда:
Закон Хаббла (продолжение)
Интерпретируя сдвиг длин волн как результат эффекта Допплера, скорость галактик пропорциональна этому сдвигу
На самом деле это не эффект Допплера!!!
Итак, скорость удаления галактики пропорцио-нальна расстоянию до неё
Значит ли это, что вблизи нашей Галактики произошел гигантский взрыв?
Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Описание слайда:
Закон Хаббла
Итак, в случае линейной зависимости удаление всех тел не означает существования центра расширения
Все тела удаляются от всех!
Но когда-то тела были ближе... Может даже все галактики, вся Вселенная расширяется из одной точки...
Слайд 9

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 10

Описание слайда:
Красное смещение
Сдвиг длины волны определяют как
z = ( – 0) / 0, где
0 – длина волны, измеренная в лаборатории
– наблюдаемая длина волны
Обычно ее называют красным смещением, так как
Если z > 0, то > 0 – линия сдвигается в сто-рону больших длин волн («красная» сторона)
В космологии чаще всего z > 0
Слайд 11

Описание слайда:
Красное смещение
Причины для изменения длины волны
Эффект Допплера (взаимное движение источника и наблюдателя)
Гравитационное смещение (различные гравитационные потенциалы источника и наблюдателя)
Расширение пространства (фотон «расши-ряется», пока движется в пространстве)
Старение фотонов (фотон «краснеет» из-за свойств пространства)
Слайд 12

Описание слайда:
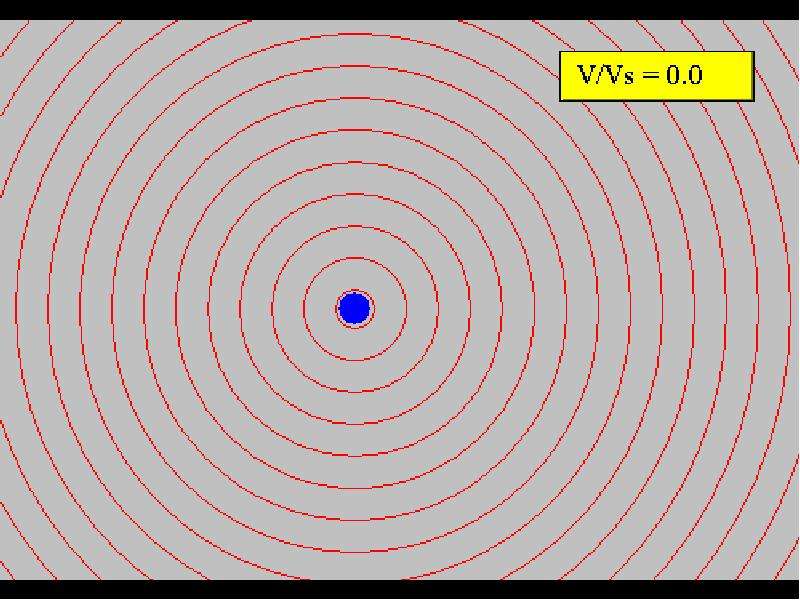
Эффект Допплера
Длина волны изменяется из-за того, что наблюдатель движется и изменяется проме-жуток времени между пучностями волны света
Из-за изменения частоты меняется и регистрируемая длина волны
При взаимном удалении источника и наблюдателя возникает красное смещение, при сближении – фиолетовое смещение
Слайд 13
Слайд 14
Слайд 15

Описание слайда:
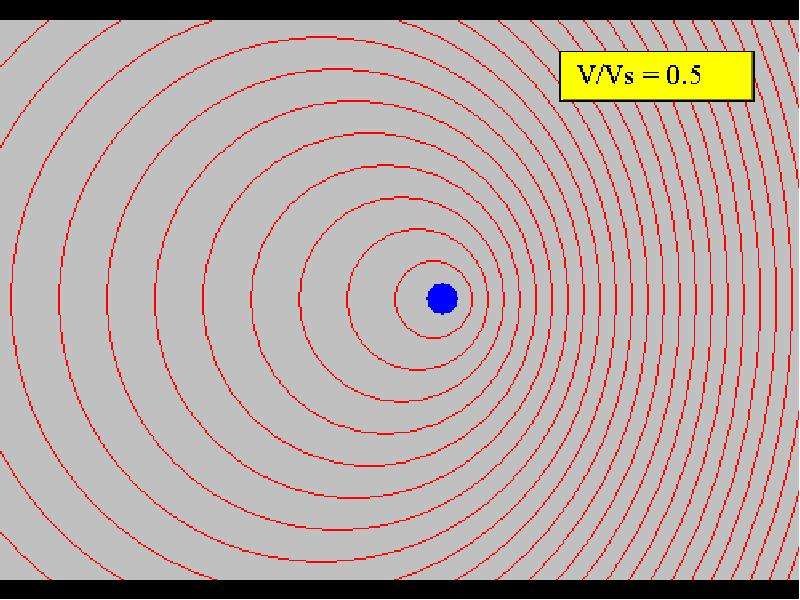
Эффект Допплера
Точная формула:
v – модуль скорости относительного движения
- угол между направлением движения источника и линией наблюдения
c – скорость света в вакууме
Примерная формула при v << c
Слайд 16

Описание слайда:
Расширение пространства
Длина волны изменяется, так как в течение свободного движения фотона пространство успело расшириться и «растянуть» фотон
При расширении пространства возникает красное смещение, при сжатии – фиолетовое смещение
Слайд 17

Описание слайда:
Расширение пространства
Интегральная формула:
a – масштабный фактор (показывает, во сколько раз пространство расширилось по сравнению с определенным моментом)
a2 соответсвует времени регистрации фотона, а a1 – времени излучения
Дифференциальная формула:
a = da/dt
Слайд 18

Описание слайда:
Красное смещение
Так как красное смещение галактики складывается из действия обоих эффектов, то
Причина закона Хаббла – расширение пространства, а разброс вокруг прямой даёт эффект Допплера, который вызывают случайные движения отдельных галактик относительно центра масс скопления галактик
Слайд 19

Описание слайда:
Суть постоянной Хаббла
Размерность постоянной Хаббла – км/с/Мпк или просто 1/с
Она показывает, насколько в относитель-ных единицах расширяется пространство в единицу времени
Значит, величина, обратная постоянной Хаббла, приблизительно разна возрасту Вселенной
Слайд 20

Описание слайда:
Метагалактика
Отсюда следует, что у Вселенной есть предел наблюдаемой области
Наблюдаемую часть Вселенной называют Метагалактикой
Расстояние до границы Метагалактики примерно RМ = c / H0 = 1.3·1026 м
Слайд 21

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 22

Описание слайда:
Космологические модели
Космологической моделью называют математическую модель, описывающую усредненное распределение материи в пространстве и его эволюцию
Модели делят на классы по теории, в рамках которой она построена:
Ньютоновская космология – всемирный закон притяжения
Релятивистская космология – ОТО
Слайд 23

Описание слайда:
Космологические модели
Основные предположения, на которых основываются все космологические модели:
Вселенная однородна и изотропна
Законы физики одинаковы во всей Вселенной
Применимость этих предположений следует из многих данных различных наблюдений
Слайд 24

Описание слайда:
Ньютоновская космология
Рассмотрим «типичный» шар, равномерно заполненный материей.
Пусть радиальные скорости частиц под-чиняются закону Хаббла (что неизбежно при наших предположениях):
Пусть H>0 и не зависит от пространст-венных координат (только от времени)
Слайд 25

Описание слайда:
Ньютоновская космология
Пусть в момент времени t0 координата частицы есть . Тогда эта координата меняется по закону (R(t) – масштабный фактор).
Так как , то
Слайд 26

Описание слайда:
Ньютоновская космология
Для определения зависимости R(t) и H(t) от времени, используем законы сохранения массы и полной механической энергии.
Масса шара не меняется
или, записывая по другому,
Слайд 27

Описание слайда:
Ньютоновская космология
Закон сохранения механической энергии для элемента на краю шара:
Кинетическая энергия
Потенциальная энергия
Полная энергия постоянна:
Слайд 28

Описание слайда:
Ньютоновская космология
Запишем полную механическую энергию (постоянную) в виде . Тогда
Слайд 29

Описание слайда:
Ньютоновская космология
Это уравнение вместе с начальными условиями полностью определяют R(t), т.е. все динамические свойства космологической модели.
В уравнение (*) не входит размер шара материи, поэтому его можно применять для шара любого размера, как и для всей Вселенной, равномерно заполненной веществом.
Слайд 30

Описание слайда:
Ньютоновская космология
Качественно можно оценить R(t) даже без интегрирования уравнения (*):
Слайд 31

Описание слайда:
Ньютоновская космология
Если k<0, то полная механическая энергия положительна (кинетическая больше потенциальной) и данный элемент объёма будет вечно отдаляться от начала координат.
Если k>0, то полная энергия отрицательна. Через какое-то время расширение затормозится и сменится сжатием (H<0)
k=0 – пограничный случай:
Слайд 32

Описание слайда:
Ньютоновская космология
Знак постоянной k и характер движения материи зависит от знака разности
, где
называют критической плотностью. Введём также обозначение
Слайд 33

Описание слайда:
Ньютоновская космология
Если , то расширение шара остановится и сменится сжатием.
Если , то расширение будет продолжаться вечно.
Значение критической плотности (как и сама плотность) меняется со временем, но знак разности плотностей не меняется.
Слайд 34

Описание слайда:
Ньютоновская космология
Решим уравнение эволюции (*) в случае, когда k = 0.
Слайд 35

Описание слайда:
Ньютоновская космология
Слайд 36
Описание слайда:
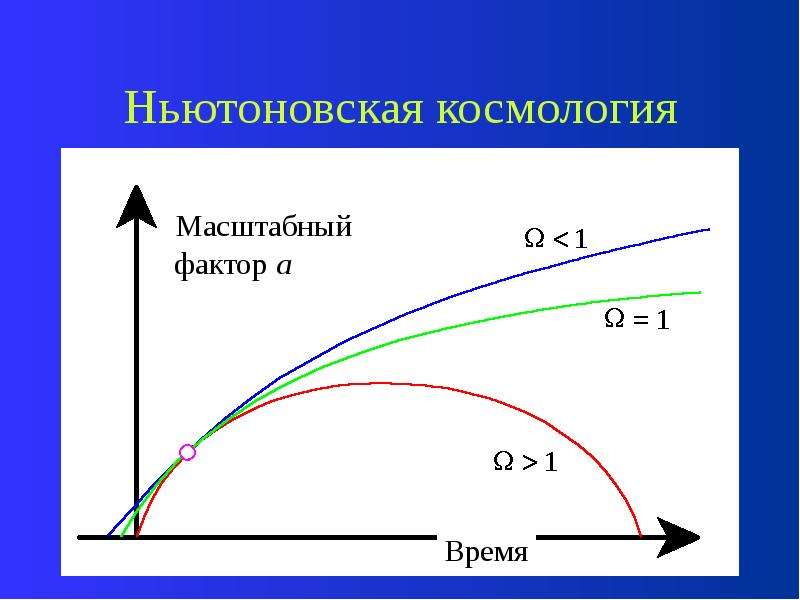
Ньютоновская космология
Слайд 37

Описание слайда:
Ньютоновская космология
Классическая космология Ньютона применима лишь малым интервалам пространства и времени (локально)
Качественно верно описывает эволюцию вселенной и ее зависимость от средней плотности
Неприменима для описания всей вселенной, так как скорость взаимо-действия считается бесконечной
Слайд 38

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 39

Описание слайда:
Релятивистская космология
Согласно экспериментальным данным, скорость света постоянна во всех системах отсчета.
Это противоречит теории Ньютона, но верно в специальной теории относительности (СТО)
Но в СТО не включено гравитационное взаимодействие. Теория, описывающая и его, учитывая конечность скорости взаимодействия, есть ОТО.
Слайд 40

Описание слайда:
История
В 1916 году А. Эйнштейн создает общую теорию относительности (ОТО)
Она рассматривает объекты, которые движутся с большими скоростями в сильных гравитационных полях
Он (и другие) ищут решения ОТО для описания эволюции Вселенной
Вселенную представляют однородной и изотропной (космологический принцип)
Слайд 41

Описание слайда:
История
В 1917 году А. Эйнштейн создает модель стационарной вселенной, дополняя урав-нения гравитационного поля «-членом»
В 1917 году В. де Ситтер находит реше-ние для динамической пустой вселенной
Закон Хаббла (1929 г.) соответствует ожиданиям ОТО и соответствует случаю расширения Вселенной
Слайд 42

Слайд 43

Описание слайда:
История
В 1922 году А.А. Фридман и, независимо от него, в 1927 году Г.Е. Леметр развили далее модель нестационарной вселенной, учитывая массу, гравитацию и кривизну пространства
Согласно этой теории вселенная расширя-ется из начальной пространственно-вре-менной сингулярности до современного состояния и дальше
Слайд 44

Слайд 45

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 46

Описание слайда:
Основные понятия
Основные понятия ньютоновской теории гравитации
Однородное и изотропное пространство, в котором происходит движение
Однородное время как параметр движения
Движущаяся масса
Гравитационное взаимодействие, моментально действующее по закону
Слайд 47

Описание слайда:
Основные понятия
Основные понятия СТО
Пространство-время Минковского
Инерциальная система отсчета (ИСО)
Скорость света c, с которой распространяются взаимодействия
Что отсутствует в этой теории
Гравитационное поле
Слайд 48

Описание слайда:
Основные понятия ОТО
Локально-инерциальная система отсчета (ЛИСО), которая вводится из-за невозможности построения единой глобальной ИСО в пространстве с гравитационным полем.
В СТО ускорение тела может быть скомпенсировано ускорением система отсчета. В ОТО это невозможно.
Слайд 49

Описание слайда:
Основные понятия ОТО
Пространство-время Римана – кривое 4-х мерное пространство (т.е. элемент интервала ds нельзя глобально преобразовать в форму Минковского)
Геометрические свойства (кривизну) определяет движение и распределение массы. Но и само движение определя-ется кривизной пространства.
Слайд 50
Описание слайда:
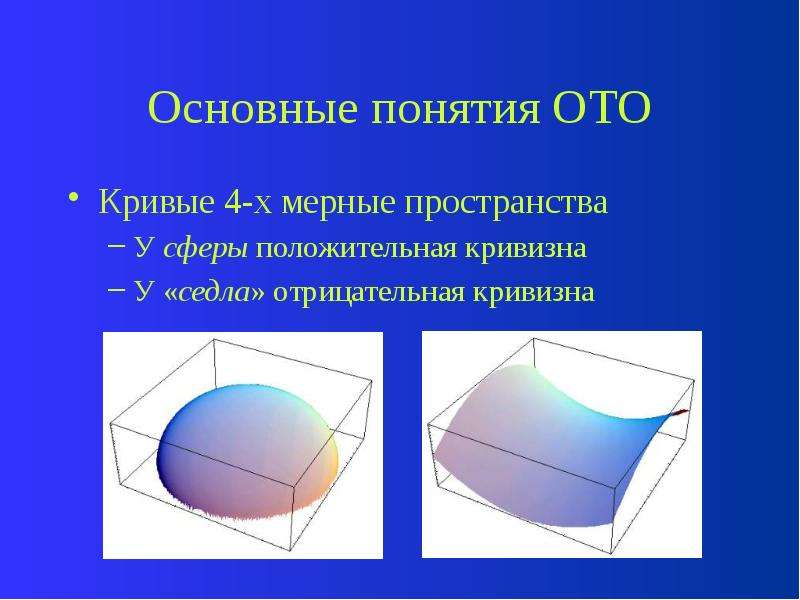
Основные понятия ОТО
Кривые 4-х мерные пространства
У сферы положительная кривизна
У «седла» отрицательная кривизна
Слайд 51
Слайд 52

Описание слайда:
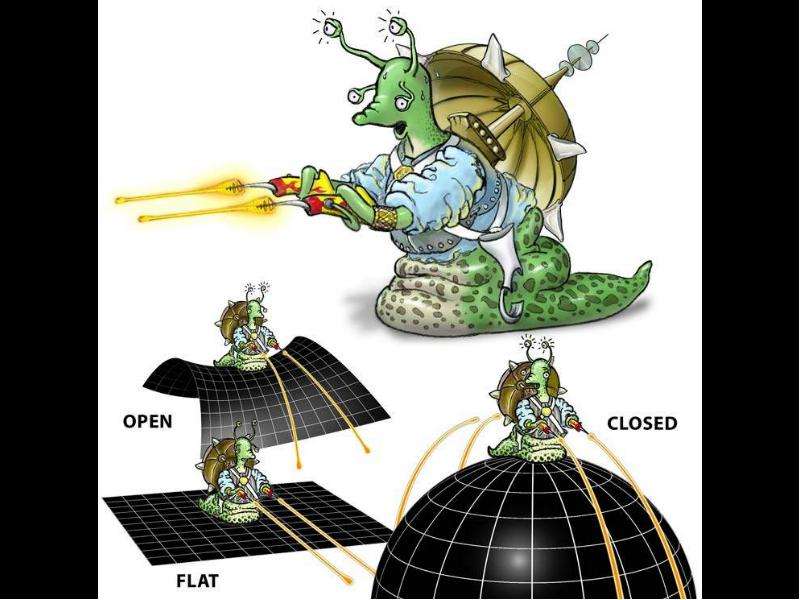
Основные понятия ОТО
Согласно ОТО, гравитационное поле проявляется в кривизне пространства. Чем больше отличие от плоского пространства, тем сильнее поле.
Уравнения гравитационного поля ОТО – система десяти нелинейных дифференциальных уравнений второго порядка
Слайд 53

Описание слайда:
Уравнения Эйнштейна
Кривизну с распределением массы связывают уравнения Эйнштейна
Rik и R=gikRik характеризуют кривизну
gik – метрический тензор
Tik характеризует распределение и движение материи
– постоянная Эйнштейна
Слайд 54

Описание слайда:
Тензор энергии-импульса
Рассмотрим вид тензора энергии-импульса Tik в наиболее частых случаях
Компонента T00 равна плотности энергии вещества = c2
Компоненты Tii (i = 1, 2, 3) равны давлению вещества p
Недиагональные члены в ЛИСО – нули
Слайд 55

Описание слайда:
Тензор энергии-импульса
Тензор энергии-импульса для пыли:
Пыль определена как среда с низкой темпе-ратурой (т.е. тепловые скорости движения много меньше скорости света с)
Отсюда давление пыли равно нулю и единственная ненулевая компонента тензора Tik есть
Слайд 56

Описание слайда:
Тензор энергии-импульса
Тензор энергии-импульса для ультра-релятивистских частиц:
Их 4-импульс равен
Тогда , где - плотность энергии
И
Слайд 57

Описание слайда:
Тензор энергии-импульса
Открытый вид тензора энергии-импульса для ультра-релятивистского вещества (в его системе отсчета):
Для излучения (фотонов) Tik такой же!
Слайд 58

Описание слайда:
Уравнение состояния
Давление с плотностью вещества связано уравнением вещества, общий вид которого p = c2
Из вида тензора Tik следует, что для пыли = 0, а для ультра-релятивистского вещества и излучения = 1/3
Слайд 59

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 60

Описание слайда:
Фридмановские модели
Основные приближения
Пространство однородно и изотропно
Описание системы происходит в ЛИСО
Тогда уравнения Эйнштейна сводятся к
Слайд 61

Описание слайда:
Фридмановские модели
Основные приближения
Пространство однородно и изотропно
Материя есть «пыль»
Тогда уравнения Эйнштейна сводятся к
Слайд 62

Описание слайда:
Фридмановские модели
Эти уравнения не независимы, и второе из них эквивалентно уравнению (*), если на место T00 подставить его значение c2
Слайд 63

Описание слайда:
Фридмановские модели
Хотя уравнения математически иден-тичны, они описывают разную «физику»
Слайд 64

Описание слайда:
Фридмановские модели
Но так как уравнения идентичны, то и решения тоже одинаковы!
Слайд 65

Описание слайда:
Эволюция Вселенной
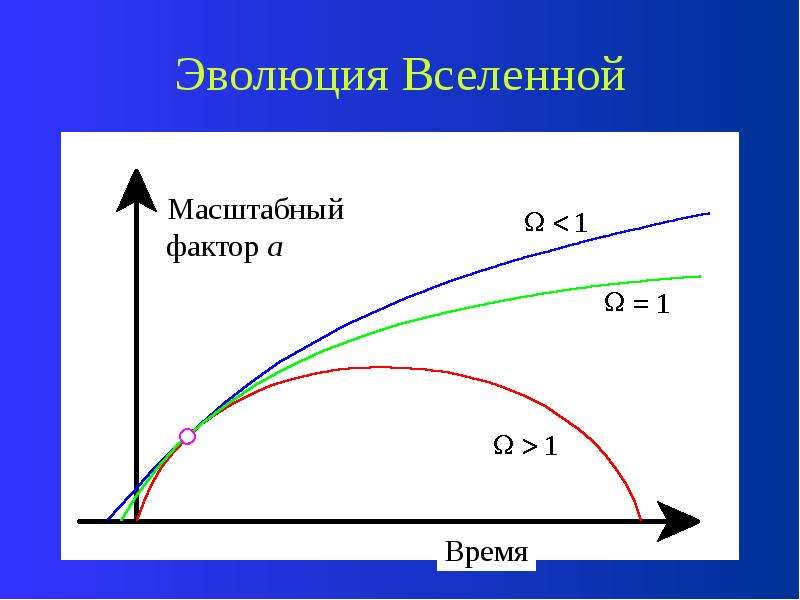
Эволюция зависит от одного параметра – параметра плотности .
Если < 1, то вселенная вечно расширя-ется. Пространство открыто.
Если > 1, то вселенная после стадии расширения начинает сжиматься обратно. Пространство замкнуто.
Если = 1, то пограничный случай – пространство плоское
Слайд 66
Описание слайда:
Эволюция Вселенной
Слайд 67

Описание слайда:
Эволюция Вселенной
Постоянная Хаббла – мера скорости изменения масштаба Вселенной а:
Со временем она меняется!
При наблюдении объекта рассчитанная постоянная Хаббла зависит от эволюции вселенной во все моменты между излучением и регистрацией фотона
Слайд 68

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 69

Описание слайда:
Наша Вселенная
Мы рассмотрели общую схему эволюции вселенной, заполненной пылевидной материей
Возникает закономерный интерес – годится ли разработанная теория для описания нашей Вселенной
И если годится, то каковы реальные значения параметров модели?
Слайд 70

Описание слайда:
Наша Вселенная
Преобразуем уравнение Фридмана (УФ), учитывая форму Tik (Tik). Итак,
Оно показывает, что эволюция зависит от уравнения состояния p = c2
Слайд 71

Описание слайда:
Наша Вселенная
Во Вселенной одновременно есть типы материи с разными значениями
Последние данные (WMAP, февраль 2003 года) убедительно показывают, что около 2/3 от общей энергии занимает т.н. тёмная энергия
Попробуем понять, что же это такое!
Слайд 72

Описание слайда:
- член
Исторически первая модель вселенной Эйнштейна (1917 г.) была по построению статичной. Однако, как мы видели, уравнения Эйнштейна не допускают такое решение
Чтобы решить это противоречие, Эйнштейн добавил в уравнения дополни-тельный скалярный член (т.н. -член)
Слайд 73

Описание слайда:
- член
Уравнения Эйнштейна:
Уравнения, дополненные -членом
Слайд 74

Описание слайда:
- член
Найдём эффективное уравнение состоя-ния -члена. Для этого представим себе, что материи вообще нет. Тогда
Эффективный тензор энергии-импульса в ЛИСО есть
Слайд 75

Описание слайда:
- член
Сравнивая с общим видом тензора энергии импульса в ЛИСО, т.е.
видим, что для -члена = – 1.
Значит, если плотность энергии -члена доминирует, то Вселенная расширяется ускоренно!
Слайд 76

Описание слайда:
- член
Действительно, из уравнения Фридмана:
Если = – 1 (т.е. всю плотность энергии составляет -член), то d2a/dt2 положите-лен и расширение происходит ускоренно.
Причина – сильное отрицательное «давление»
Слайд 77

Описание слайда:
Наша Вселенная
Итак, обычное вещество с 0 способствует сжатию Вселенной, а -член – ее расширению.
Так как в нашей Вселенной доминирует -член, то она будет расширятся вечно и ускоренно.
Пока на ясна физическая причина существования ненулевого -члена. К примеру, это могла бы быть энергия вакуумных нулевых флуктуаций...
Слайд 78

Описание слайда:
2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей
Слайд 79

Описание слайда:
Модель эволюции Вселенной
Обобщим закономерности, выведенные на этой лекции
Выведем зависимости характеристик вещества от времени для
Пыли
Ультра-релятивистского вещества и излучения
Космологической постоянной
Слайд 80

Описание слайда:
Состояния вещества
Пыль:
Плотность энергии
Давление p = 0, = 0
Ультра-релятивистское вещество и излучение:
Плотность энергии = c2
Давление p = 1/3 , = 1/3
Космологическая постоянная :
Плотность энергии =
Давление p = -, = -1
Слайд 81

Описание слайда:
Плотность энергии
Уравнение, описывающее зависимость плотности энергии от масштабного фактора a:
Слайд 82

Описание слайда:
Плотность энергии
Слайд 83

Описание слайда:
Масштабный фактор
Уравнение Фридмана описывает зависи-мость масштабного фактора от времени:
Слайд 84

Описание слайда:
Масштабный фактор
Если -1, то
Если = -1, то
Слайд 85

Описание слайда:
Постоянная Хаббла
Если a(t) – степенная функция, то посто-янная Хаббла обратно пропорциональна времени
Если a(t) – экспонента, то постоянная Хаббла не зависит от времени
Слайд 86

Описание слайда:
Температура
Зависимость температуры излучения от а есть , так как плотность энергии излучения есть
Зависимость температуры пыли от времени не так проста, так как на нее влияют эффекты выделения внутренней энергии (притяжение, ядерные и химические реакции и др.)
Слайд 87

Описание слайда:
Параметры вещества
Слайд 88

Описание слайда:
Выводы
Узнали главные экспериментальные факты внегалактической астрономии
Ознакомились с некоторыми моделями эволюции Вселенной на основе теории Ньютона и ОТО
На следующей лекции проследим эволюцию Вселенной с точки зрения теории Большого Взрыва
Слайд 89

Описание слайда:
Спасибо за внимание!
Презентацию на
тему Космология можно скачать бесплатно ниже: