🗊Презентация Алгоритм кластеризації k-means (1)

Алгоритм кластеризації k-means (1) <number> Задано набір з 8 точок у двовимірному просторі, який треба розбити на два кластери: Крок 1. Визначимо кількість кластерів, на яку треба розбити початкову множину: k=2. Крок 2. Випадковим чином визначимо дві точки m1=G і m2=Н, як центри кластерів. Крок 3, прохід 1. Для кожної точки визначимо найближчий до неї центр кластеру у евклідовій метриці, тим самим визначаючі, до якого кластеру вона відноситься. Визначивши належність точок кластерам, обчислюємо суму квадратів помилок:

Алгоритм кластеризації k-means (2) <number> Крок 4, прохід 1. Обчислюємо центроїди, до яких переміщаються центр кластерів: Ц1= [(1+1+1/3);(3+2+1/3)]=(1;2); Ц2=[(3+4+5+4+2/5);(3+3+3+2+1/5)]=(3,6;2,4). Крок 3, прохід 2. Для кожної точки знов визначається найближчий до неї центр нових кластерів і відповідна належність її до цього кластеру: Бачимо, що відносно велика зміна значення m2 призвела до того, що точка Н стала ближче до центру m1 ставши членом кластеру 1. Нова сума квадратів помилок склала: Помилка зменшилось, що означає краще групування об’єктів відносно центрів кластерів.

Алгоритм кластеризації k-means (3) <number> Крок 4, прохід 2. Обчислюємо нові центроїди для кожного кластеру: Ц1= [(1+1+1+2/4);(3+2+1+1/4)]=(1,25;1,75); Ц2= [(3+4+5+4/4);(3+3+3+2+/4)]=(4;2,75). У порівнянні з минулим проходом центри кластерів мало змінилася. Крок 3, прохід 3. Визначаємо відстані точок від ближчого з центрів нових кластерів: Нова сума квадратів помилок склала: Сума квадратів помилок мала змінилась відносно попереднього проходу. Крок 4, прохід 3. Обчислюємо нові центроїди кластерів. Оскільки жодний об’єкт не змінив свого членства у кластерах і положення центроїдів практично не змінилося,алгоритм завершує свою роботу.

Наївний Байєсовький класифікатор (1) <number> Для заданого набору даних, з використанням наївного байєсовського класифікатора визначте, який статус ймовірно має особа (а) з відділу маркетингу у віці від 31 до 35 років, з зарплатою від 46 до 50 тисяч на місяць; (б) з відділу продажів у віці від 31 до 35 років, з зарплатою від 66 до 70 тисяч на місяць Р(A&B)=P(A)P(B|A)=P(B)P(A|B); P(B|A)=P(B)P(A|B)/P(A); Відповідь: А) Р(старш|маркет; 31-35; 46-50)= Р(старш) Р(маркет|старш) Р(31-35|старш) Р(46-50|старш) = 5/11х1/5х2/5х2/5 = 0,0145 Р(молод|маркет; 31-35; 46-50)= Р(молод) Р(маркет| молод) Р(31-35| молод) Р(46-50| молод)= 6/11х1/6х2/6х2/6 = 0,0101 Р(старш|маркет;31-35;46-50)= 0,0145/(0,0145+0,0101)= 0,0145/0,0246=0,59 Р(молод|маркет;31-35;46-50)= 0,0101/(0,0145+0,0101)= 0,0101/0,0246=0,41 В) Р(старш|продаж; 31-35; 66-70)= Р(старш) Р(продаж|старш) Р(31- 35|старш) Р(66-70|старш) = 5/11х1/5х2/5х2/5 = 0,006 Р(молод|продаж;31-35;76-70)= Р(молод) Р(продаж| молод) Р(31-35| молод)Р(66-70| молод)= 6/11х2/6х2/6х0/6= 0 Р(старш|продаж; 31-35; 66-70)=1 Р(молод|продаж; 31-35; 76-70)=0

ДЕРЕВА РІШЕНЬ (1) <number> На основі навчальної вибірки побудуйте дерево рішень для визначення бажання різних категорій споживачів щодо купівлі комп’ютера I(SТАК, SНІ )= I(9,5)= -9/14 log2(9/14) – 5/14 log2(5/14)=0.94 Вік: 3 значення: <=30 (2 так,3 ні), 31..40 (4 так,0 ні), >40 (3 так,2 ні)

ДЕРЕВА РІШЕНЬ (2) <number> На основі навчальної вибірки побудуйте дерево рішень для визначення бажання різних категорій споживачів щодо купівлі комп’ютера I(SТАК, SНІ )= I(9,5)= -9/14log(9/14) – 5/14log(5/14)=0.94 Вік: 3 значення: <=30 (2 так,3 ні), 31..40 (4 так,0 ні), >40 (3 так,2 ні) Entropy(вік) = 5/14 (-2/5 log(2/5)-3/5log(3/5)) +4/14 (0) + 5/14 (-3/5log(3/5) 2/5log(2/5)) = 5/14(0.9709) + 0 + 5/14(0.9709) = 0.6935 Gain(age) = 0.94 – 0.6935 = 0.2465 Дохід 3 значення: високий (2так,2ні), середній (4так,2ні), низький (3так,1ні) Entropy(дохід) = 4/14(-2/4log(2/4)-2/4log(2/4)) + 6/14 (-4/6log(4/6)-2/6log(2/6)) + 4/14 (-3/4log(3/4)-1/4log(1/4)) = 4/14 (1) + 6/14 (0.918) + 4/14 (0.811)= 0.285714 + 0.393428 + 0.231714 = 0.9108 Gain(дохід) = 0.94–0.9108=0.0292 Студент: 2 значення: так (6 так, 1 ні), ні (3 так, 4 ні) Entropy(студент) = 7/14(-6/7log(6/7)) + 7/14(-3/7log(3/7)-4/7log(4/7) = 7/14(0.5916) + 7/14(0.9852) = 0.2958 + 0.4926 = 0.7884 Gain (студент) = 0.94 – 0.7884 = 0.1516 Кредит: 2 значення: гарна (6 так, 2 ні), відмінна (3 так, 2 ні) Entropy(кредит) = 8/14(-6/8log(6/8)-2/8lo g(2/8)) + 6/14(-3/6log(3/6)-3/6log (3/6)) = 8/14(0.8112) + 6/14(1) = 0.4635 + 0.4285 = 0.8920 Gain(кредит) = 0.94 – 0.8920 = 0.048

ДЕРЕВА РІШЕНЬ (3) <number> Ентропія блоку: I(SТАК, SНІ)= I(2,3)= -2/5 log(2/5) – 3/5 log(3/5)=0.97 Дохід: 3 значення: високий (0так,2 ні),середній (1так,1 ні),низький (1так,0ні) Entropy(дохід) = 2/5(0) + 2/5 (-1/2log(1/2)-1/2log(1/2)) + 1/5 (0) = 2/5 (1) = 0.4 Gain(дохід) = 0.97 – 0.4 = 0.57 Студент: 2 значення: так (2 так, 0 ні), ні (0 так, 3 ні) Entropy(студент) = 2/5(0) + 3/5(0) = 0 Gain (student) = 0.97 – 0 = 0.97 Можна робити розбиття по атрибуту студент без перевірки інших атрибутів, оскільки значення показника Gain для атрибуту Студент є максимальним

ДЕРЕВА РІШЕНЬ (4) <number> Ентропія блоку: I(SТАК, SНІ)= I(3,2)= -3/5log(3/5) – 2/5log(2/5)=0.97 Дохід: 2 значення: середній (2 так, 1 ні), низький (1 так, 1ні) Entropy(дохід) = 3/5(-2/3log(2/3)-1/3log(1/3)) + 2/5 (-1/2log(1/2)-1/2log(1/2)) = 3/5(0.9182)+2/5 (1) = 0.55+0. 4= 0.95 Gain(income) = 0.97 – 0.95 = 0.02 Студент: 2 значення: так (2 так, 1 ні), ні (1 так, 1 ні) Entropy(студент)=3/5(-2/3log(2/3)-1/3log(1/3))+2/5(-1/2log(1/2)-1/2log(1/2))= 0.95 Gain (student)=0.97–0.95 = 0.02 Кредит: 2 значення: гарна (3 так, 0 ні), відмінна (0 так, 2 ні) Entropy(кредит) = 0 Gain(кредит) = 0.97 – 0 = 0.97 Здійснюємо розбиття по атрибуту КРЕДИТ, яке дасть два чисті класи:

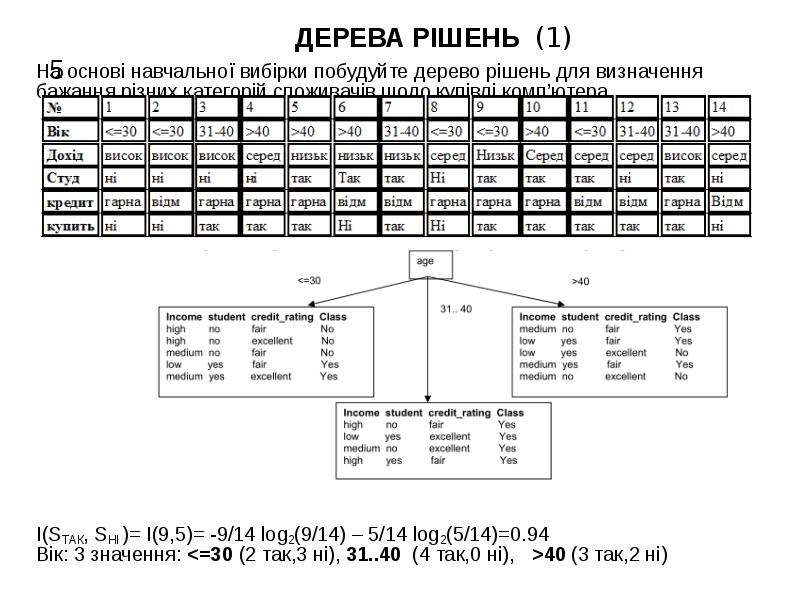
АСОЦІАТИВНІ ПРАВИЛА (1) <number> T1{M,O,N,K,E,Y}; T2{D,O,N,K,E,Y}; T3{M,A,K,E}; T4{{M,U,C,K,Y}; T5{C,O,O,K,I,E};підтримка – 60%; довіра – 80%. ПРАВИЛА: A→B: P(B|A)=|B∩A|/|A| o,k→e [0,6;1]; o,e→k[0,6;1]; k,e→o[0,6;0,75] m→ k [0,6;1]; k→m [0,6;0,6] o→k [0,6;1] k→o [0,6;0,6] o→e [0,6;1]; e→o[0,6;0,75]; y→k[0,6;1] Відповідь: o→k,e [0,6;1]; o,k→e [0,6;1]; o,e→k[0,6;1]; m→ k [0,6;1]; o→k [0,6;1]; o→e [0,6;1]; y→k[0,6;1]

МЕРЕЖА КОХОНЕНА (1) <number> Розглянемо приклад роботи мережі Кохонена, що містить 2 х 2 нейрона у вихідному шарі, а множина даних представлена атрибутами Вік і Дохід з попередньо нормалізованими даними. У зв’язку з малим розміром мережі встановимо радіус навчання R=0, тобто можливість підстроювати ваги буде надаватися лише нейрону-переможцю. Коефіцієнт швидкості навчання встановимо =0,5.

МЕРЕЖА КОХОНЕНА (2) <number>

МЕРЕЖА КОХОНЕНА (3) <number>

ГЕНЕТИЧНІ АЛГОРИТМИ (1) <number> Знайдіть найкраще розташування вершин графу, за умов розміщення їх в один ряд, після трьох циклів роботи ГА при заданому початковому наборі хромосом. Якість розміщення оцінюється сумою довжини ребер графа. Єдиною операцією, що здійснюється на кожній ітерації роботи алгоритму є мутація, яка застосовується до кращої хромосоми покоління по розряду, який відповідає номеру ітерації і полягає у інверсії порядку розташування значень всіх генів хромосоми, розташованих за вибраним для мутації. Оцініть якість кожної з отриманих популяцій. 1.Розміщаємо хромосоми відповідно з генами (номерами вершин) хромосом. 2. Кількість горизонтальних відрізків між вершинами: L1=3+4+2+2=11, L2=1+2+3+3=9, L3=1+2+2+4=9. Хромосома 2 є найменшою. Піддаємо її мутації оператором інверсії по першому елементу. Тобто перша вершина залишається на своєму місці, а інші записуються у зворотному порядку: 25431. Довжина ребер: L4=1+2+3+2=2. Отож, міняємо L1 на L4 і отримуємо другу популяцію. Краща хромосома після мутації набуде вигляду: 25134 з довжиною 8. Третя популяція:

ГЕНЕТИЧНІ АЛГОРИТМИ (2) <number> Задано початкову популяцію з 4 хромосом, кожна з яких має по 2 гени x i y. Пристосованість хромосоми оцінюється функцією Z. При однакових Z перевагу має хромосома з більшим номером. На кожній ітерації найкраща хромосома a породжує 4 нові хромосоми b1,c1,b2,c2, схрещенням з хромосомами b i c з більш низькими значеннями Z за схемою, наведеною на рисунку. Хромосома з найгіршою пристосованістю вилучається з популяції. Знайдіть показник найкращої пристосованості хромосоми в популяції и значення середньої пристосованості популяції після 3-х етапів еволюції.

ГЕНЕТИЧНІ АЛГОРИТМИ (2) <number>

ГЕНЕТИЧНІ АЛГОРИТМИ (3) <number>

ГЕНЕТИЧНІ АЛГОРИТМИ (4) <number>