🗊Презентация Автоматы и формальные языки

Автоматы и формальные языки

Структура курса Конечные автоматы-распознаватели – 4 л Лекция 1. Формальные языки. Примеры языков. Грамматики. КА Лекция 2. Теория конечных автоматов-распознавателей Лекция 3. Трансляция автоматных языков Лекция 4. Регулярные множества и регулярные выражения Порождающие грамматики Хомского – 3 л Атрибутные трансляции и двусмысленные КС-грамматики – 2 л Распознаватели КС-языков и трансляция – 6 л Дополнительные лекции 2 л

Формальные языки

Автоматные языки Конечных автоматов-распознавателей бесконечное число. И автоматных языков тоже бесконечное число. Но существуют языки, которые не являются автоматными. Например, язык вложенных скобок L={anbn | n0} – неавтоматный.

Представление конечных автоматов

Необходимость изучения автоматных языков и конечных автоматов-распознавателей Автоматными языками являются многие языки: Специализированные языки Языки управления ОС Многие скриптовые языки Фрагменты языков высокого уровня (имена, константы, комментарии, ...) Все регулярные языки (т.е. языки, задаваемые регулярными выражениями) ... ... Автоматные языки составляют лишь подкласс (довольно узкий) всех возможных языков Примеры неавтоматных языков: - язык вложенных скобок (и любой язык, с вложенными конструкциями) - множество цепочек с одинаковым числом вхождений символов а и b - все языки программирования высокого уровня, естественные языки .... Существует множество важных и интересных практических применений автоматных языков

Примеры языков и распознающих их конечных автоматов Пример 1. Язык: цепочки из 0 и 1, заканчивающиеся на 00 Например: 0010100, 0100, 000, ...

Операции над автоматами: тримминг

Полный конечный автомат Если переходы в автомате-распознавателе под воздействием некоторых событий не определены, то это означает, что соответствующие цепочки входного языка ошибочны, они не допускаются, не принадлежат языку, распознаваемому этим автоматом. Для любых манипуляций с автоматом это состояние нужно вводить явно. Полученный полный автомат с точки зрения распознавания языка эквивалентен исходному автомату.

Приведение конечного автомата Операция “приведения” (trimming) конечного автомата: выбрасывание всех состояний, недостижимых из начального состояния, и тех, из которых недостижимо ни одно из финальных состояний (не кодостижимых). При этом язык, допускаемый автоматом, не меняется!

Распознавание дополнения автоматного языка КА А распознает цепочку, если она переводит его из начального в одно из финальных состояний. Язык LA состоит из всех допускаемых цепочек.

Распознаватель дополнения автоматного языка 1: Заданный КА с неполностью определенными переходами

Синхронная композиция двух автоматов-распознавателей Пересечение автоматных языков

Синхронная композиция автоматов – два автомата, работающие синхронно от одного входа

Синхронная композиция автоматов.

Пример. Статический анализ текста || программ Правильные цепочки событий обращения к буферу (запись, p от put и выборка, t от take) – язык (pt)* Анализ статического кода параллельной программы, работающей с буфером, может выявить любую неправильную подцепочку в потоке операций

Синтез супервизоров – новая идея построения систем логического управления Автомат А может быть использован как супервизор – устройство управления, которое ограничивает функционирование системы процессов только правильными цепочками язык (pt)*

Синтез супервизоров - “горячая” область исследований INTERNATIONAL WORKSHOP ON DISCRETE EVENT SYSTEMS IEEE INT CONFERENCE ON EMERGING TECHNOLOGIES AND FACTORY AUTOMATION CONFERENCE OF IEEE INDUSTRIAL ELECTRONICS IEEE INTERNATIONAL CONFERENCE ON ROBOTICS AND AUTOMATION …

Эквивалентность двух автоматов-распознавателей

Эквивалентность двух конечных автоматов-распознавателей – как проверить? Определение. Два конечных автомата-распознавателя эквивалентны, если языки, распознаваемые ими, совпадают

Эквивалентные автоматы-распознаватели. Теорема Мура

Эквивалентные автоматы-распознаватели

Минимизация конечных автоматов-распознавателей

Минимизация конечных автоматов-распознавателей Существует единственный (с точностью до изоморфизма, т.е. именования состояний) минимальный конечный автомат, распознающий данный автоматный язык. У КА есть его каноническое представление - это минимальный КА.

Пример неминимального автомата Подмножества состояний {0,2}; {1,5,7}; {3,6}; {4} – классы эквивалентных состояний. Как найти эту эквивалентность?

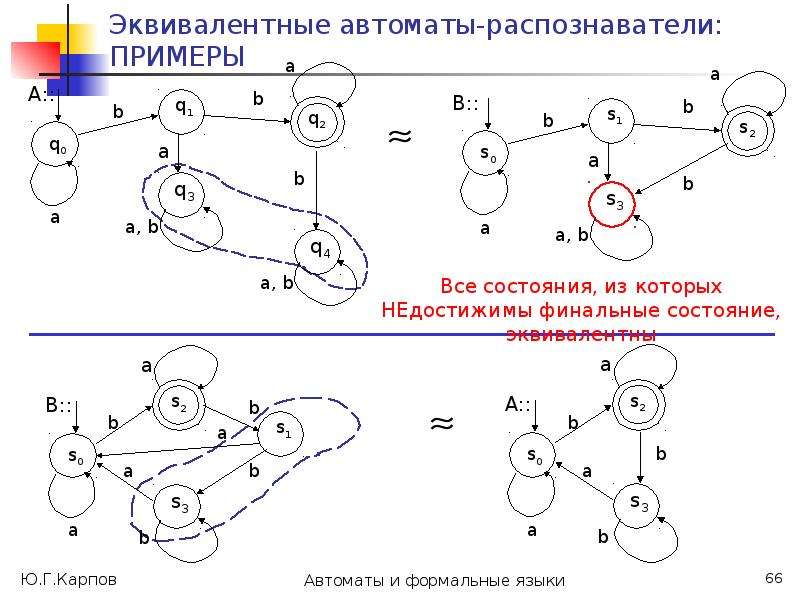
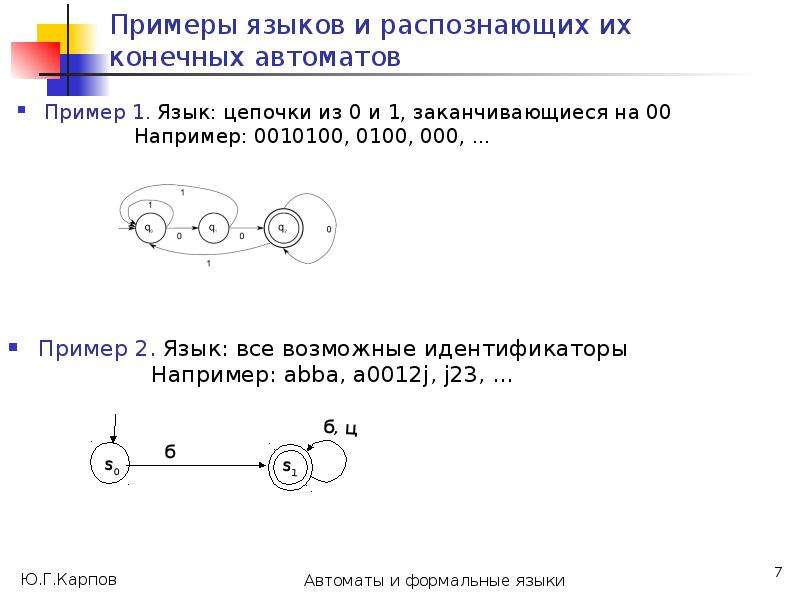
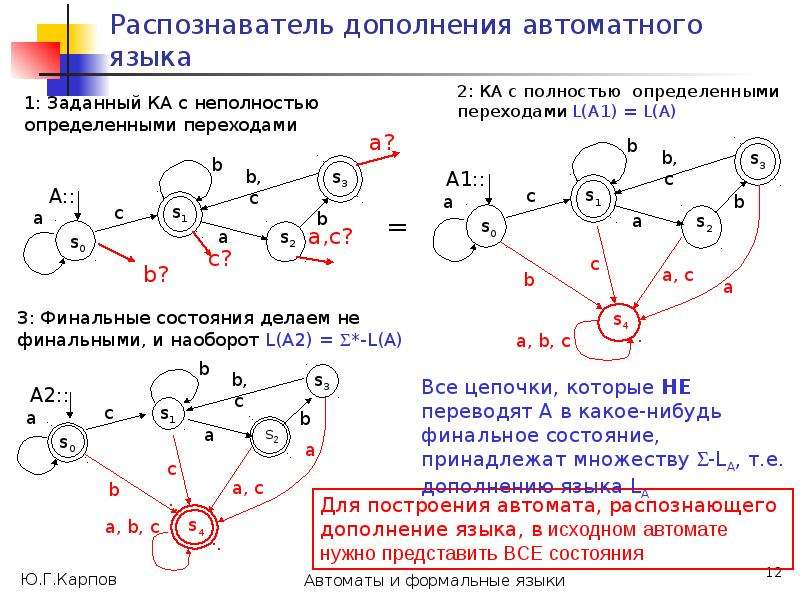
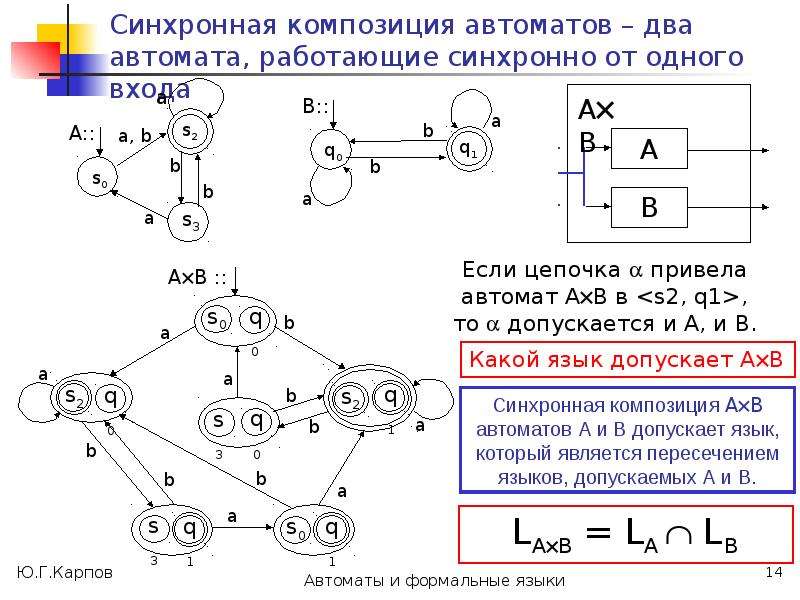
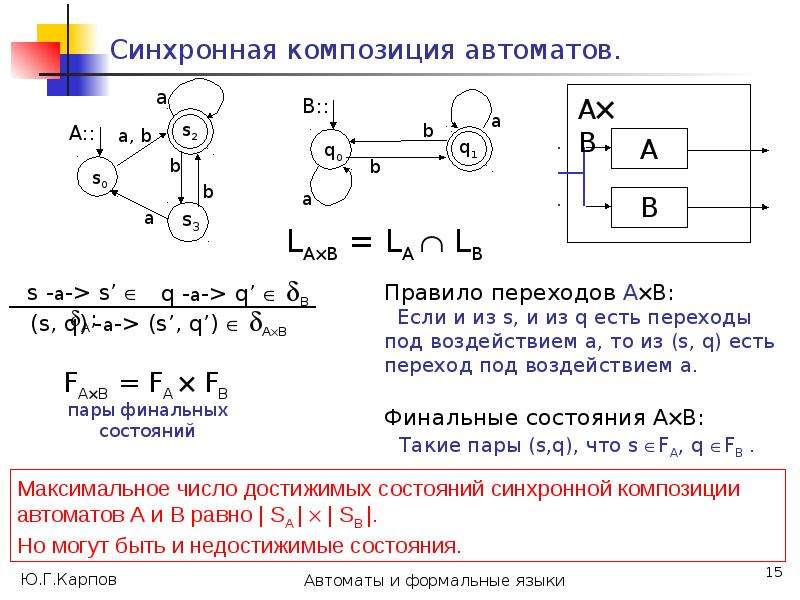
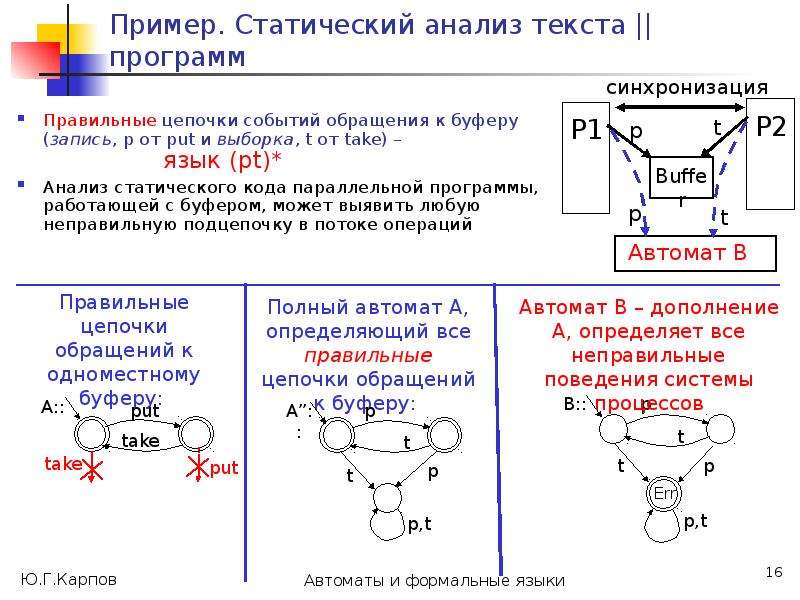
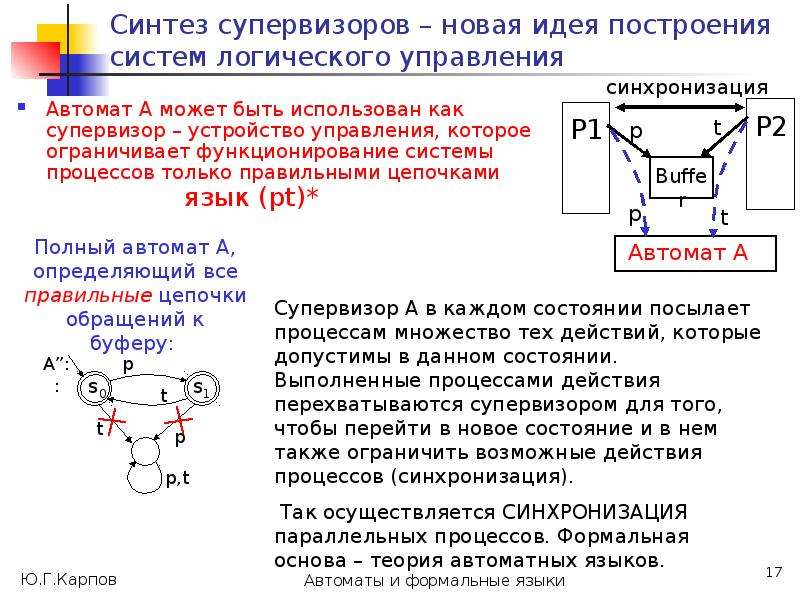
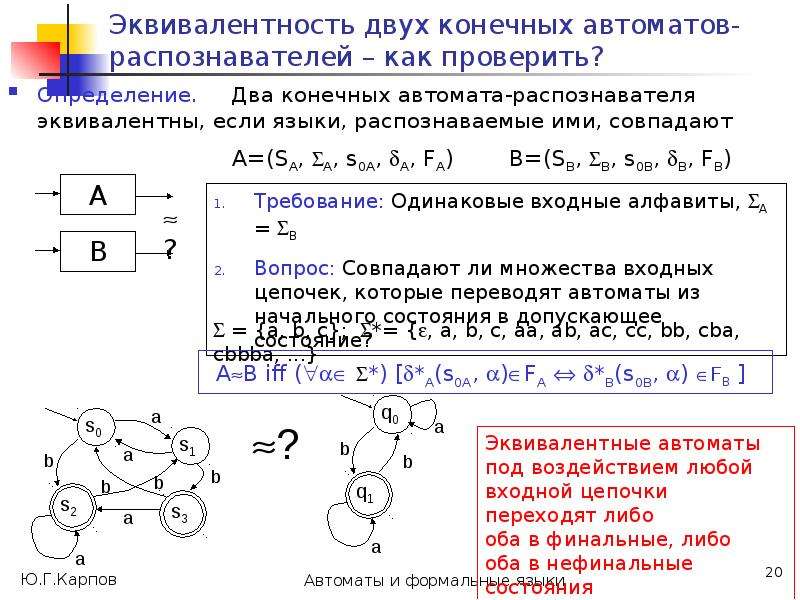
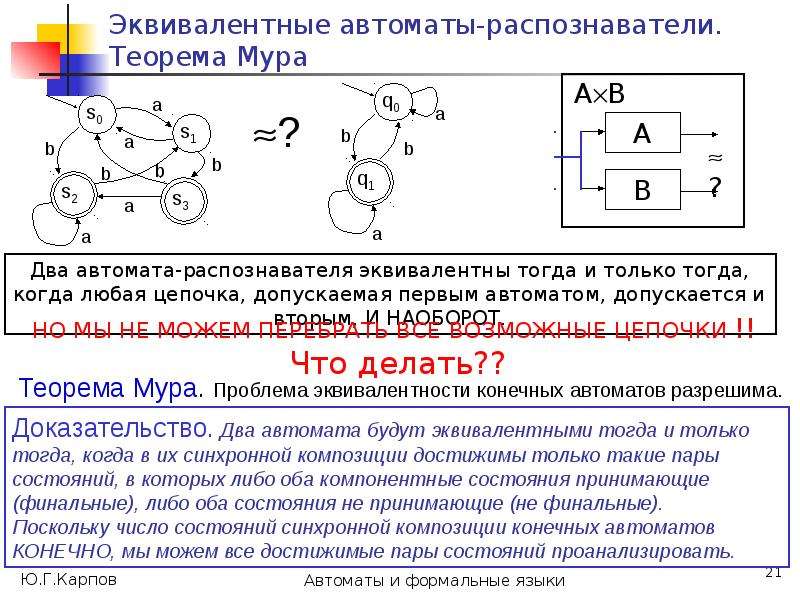
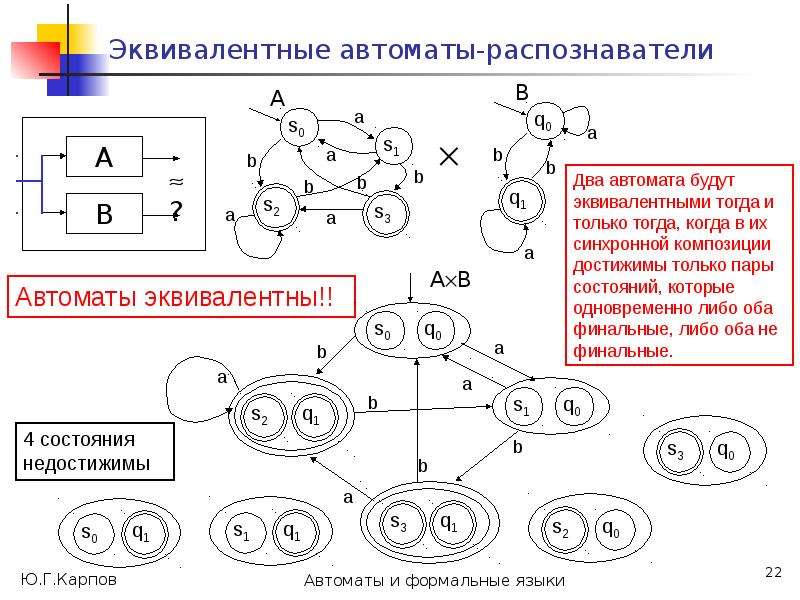
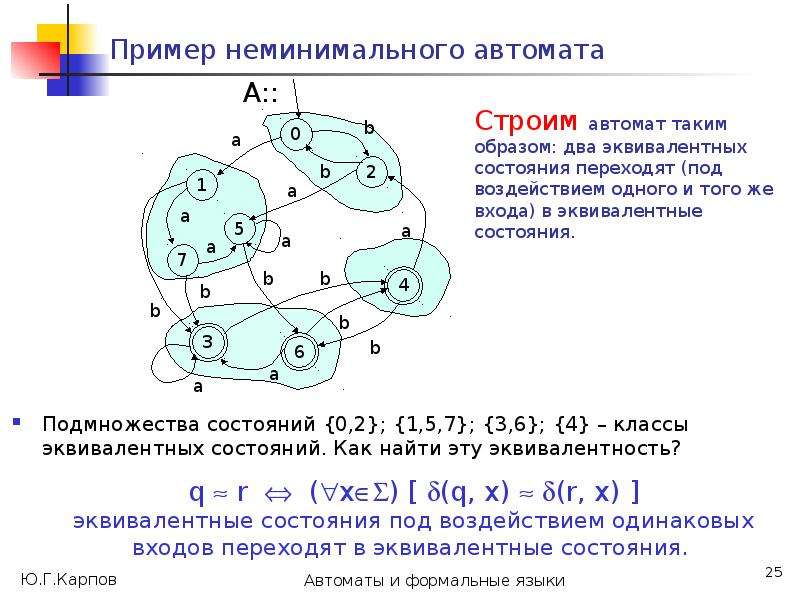
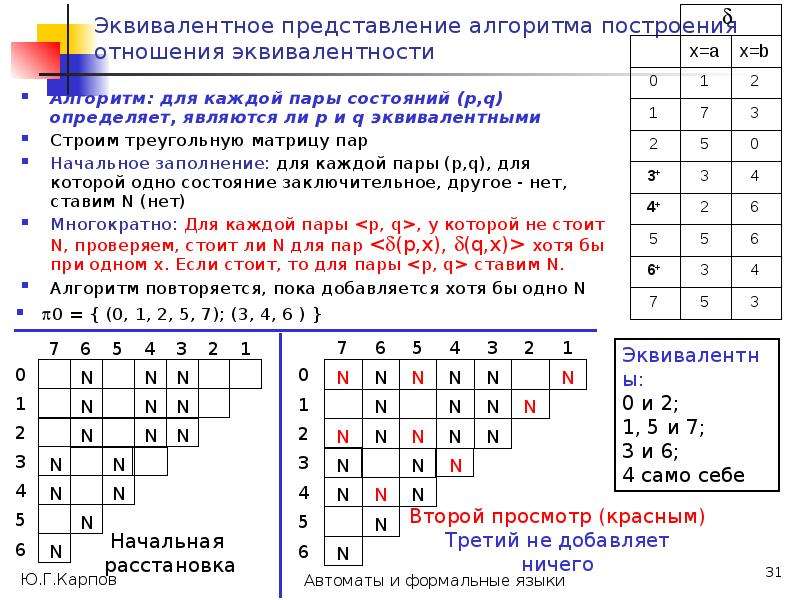
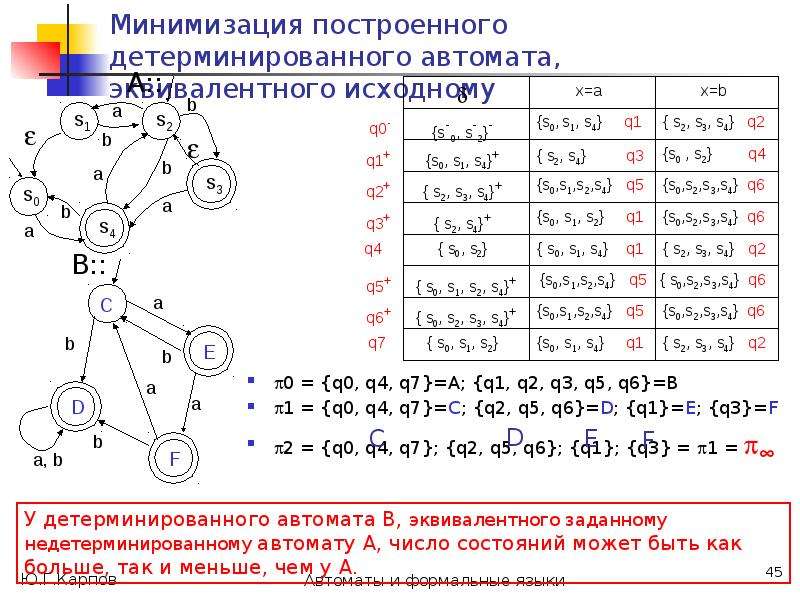
Минимизация конечных автоматов - распознавателей Построим на множестве состояний автомата А разбиения 0, 1, ..., , такие, что в один класс k попадают состояния, из которых цепочки длиной k одновременно допускаются или одновременно не допускаются. Такие состояния будем считать k-эквивалентными, т.е. p k q (в отношении k) p k q  (*:= k) [ *(p, )F  *(q, )F ] .

Конечный автомат с эквивалентными состояниями 0 = {0, 1, 2, 5, 7}=A; {3, 4, 6}=B 1 = {0, 2}=C; {1, 5, 7}=D; {3, 6}=E; {4}=F 2 = {0, 2}; {1, 5, 7}; {3, 6}; {4} = 1 = 

Алгоритм построения эквивалентности  Так же, как и для автоматов-преобразователей, рассматриваем последовательность разбиений k на классы эквивалентности. Два состояния, s и q, k-эквивалентны, если под воздействием любой входной цепочки длиной не более k, автоматы попадают оба либо в пару финальных, либо в пару нефинальных состояний. 0 всегда состоит из двух классов: все нефинальные состояния – один класс, все финальные состояния – другой. Пусть уже построено разбиение k. Два состояния, находящиеся в одном классе эквивалентности k, будут в одном классе эквивалентности k+1 тогда и только тогда, когда для любого х состояния (s,x) и (q,x) будут в одном и том же классе предыдущего разбиения k.

Минимальный конечный автомат-распознаватель 0 = {0, 1, 2, 5, 7}=A; {3, 4, 6}=B 1 = {0, 2}=C; {1, 5, 7}=D; {3, 6}=E; {4}=F 2 = {0, 2}; {1, 5, 7}; {3, 6}; {4} = 1 = 

Представление отношения эквивалентности матрицей Манипуляции с отношениями эквивалентности удобно выполнять с помощью матрицы инциденций, в которой в клетке <i, j> ставим N, если элементы i и j НЕ принадлежат одному и тому же блоку соответствующего разбиения

Эквивалентное представление алгоритма построения отношения эквивалентности Алгоритм: для каждой пары состояний (р,q) определяет, являются ли р и q эквивалентными Строим треугольную матрицу пар Начальное заполнение: для каждой пары (р,q), для которой одно состояние заключительное, другое - нет, ставим N (нет) Многократно: Для каждой пары <p, q>, у которой не стоит N, проверяем, стоит ли N для пар <(р,х), (q,х)> хотя бы при одном х. Если стоит, то для пары <р, q> ставим N. Алгоритм повторяется, пока добавляется хотя бы одно N

Недетерминированные конечные автоматы-распознаватели

Недетерминированные конечные автоматы-распознаватели Два начальных состояния, пустой переход, неоднозначный переход – как это понимать: как ошибки, коллизии? Что это за монстр? Что значит – несколько возможных переходов? Как его реализовывать? Автомат подбрасывает монету?

Основное правило для недетерминированных конечных автоматов-распознавателей Как понимать коллизии: а) несколько начальных состояний, б) несколько переходов, помеченных одним и тем же символом, в) переходы, помеченные пустым символом .

Как “работает” недетерминированный КА

Формальное определение недетерминированного КА Формальное задание автомата примера: А=(S, , s0, , F) S=(s0, s1, s2, s3, s4);  = {a, b}; S0={s0, s2} (s0, a)={s4}; (s1, b)={s4}; (s2, a)={s4}; (s2, b)={s2, s3, s4); (s3, a)={s0, s1, s4}; ... ({s2, s3, s4}, a) ={s0, s1, s3, s4); Спонтанные переходы (s1, )={s1, s0}; (s3, )={s3, s2}; F={s3, s4}.

Приведение к НДКА без -переходов

Чем удобны НДКА? Пример 1 Строим НЕдетерминированный конечный автомат:

Чем удобны НДКА? Пример 2 Задача: Построить КА с входным алфавитом  = {a, b, c}, распознающий все цепочки, которые начинаются символом а и кончаются символом с

Чем удобны НДКА? Пример 3 Задача: Построить КА с входным алфавитом  = {0, …, 9}, распознающий все числа, которые делятся на 25 (числа вводятся старшими разрядами вперед) Ясно, что это числа, заканчивающиеся на 00, 25, 50 и 75

Распознающая мощность недетерминированных КА Ясно, что детерминированные конечные автоматы – подкласс недетерминированных КА.

Распознающая мощность недетерминированных КА

От недетерминированного автомата к эквивалентному детерминированному автомату

Минимизация алгоритмом “треугольника”

Минимизация построенного детерминированного автомата, эквивалентного исходному

Пример перехода от недетерминированного автомата к эквивалентному детерминированному

Зачем нужны недетерминированные КА? Пример 2 Задача: Построить КА с входным алфавитом  = {a, b, c}, распознающий все цепочки, которые начинаются символом а и кончаются символом с.

Операции над автоматными языками и конечными автоматами-распознавателями

Операции над автоматными языками Теорема. Если L1 и L2 – автоматные языки, то автоматными являются также их объединение L1L2, пересечение L1L2. конкатенация L1L2, дополнение -L1 ,итерация L1*

Операции над автоматами и автоматными языками, дающие в результате автоматные языки LA = LA1  LA2

Резюме: операции над автоматными языками Теорема. Множество автоматных языков замкнуто относительно операций: - дополнения, - объединения, - пересечения, - конкатенации, - итерции (звезда Клини).

Пример применения недетерминированных КА: Римская система счисления

Что написано на золотой медали Альфреда Нобиля?

Зачем нужны недетерминированные КА? Пример

Правила построения римских чисел: Википедия Если меньшие цифры следуют за большими, то их значения суммируются. Только цифры, являющиеся степенью 10, могут повторяться до 3-х раз (т.е. V, L и D повторяться не могут), любые цифры могут отсутствовать. Меньшие цифры могут предшествовать большим. Значение числа получается вычитанием меньшей цифры из большей. Такое предшествование возможно в следующих случаях: меньшая цифра может быть только степенью 10 (т.е. C, X, I); ее значение может быть только либо одной пятой либо одной десятой значения большей (например, можно XL (=40) и XC (=90), но XM и XD – нельзя); она либо первая цифра в числе, либо ей предшествует цифра, значение которой, по крайней мере, в 10 раз больше ее значения (например, MXL(=1040) можно, LXL – нельзя); если за большей цифрой следует какая-либо цифра, она должна быть меньше, чем та, которая предшествует большей цифре.

Правила построения римских чисел: формально (1) Меньшие цифры обычно следуют за большими.

Правила построения римских чисел: формально (2) Меньшие могут предшествовать большим. Меньшая цифра: может быть только степенью 10 (т.е. C, X, I); ее значение может быть только либо одной пятой либо одной десятой значения большей.

Правила построения римских чисел: формально (3) Меньшая цифра либо первая в числе, либо ей предшествует цифра, значение которой, по крайней мере, в 10 раз больше ее значения. Если за большей цифрой следует какая-либо цифра, она должна быть меньше, чем та, которая предшествует большей цифре.

Возможные значения римских чисел

Правила построения римских чисел: формально (4)

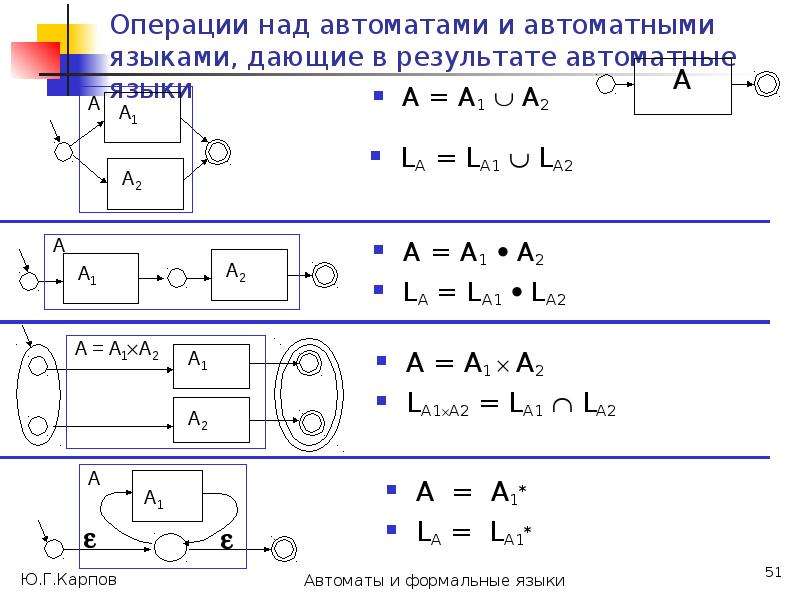
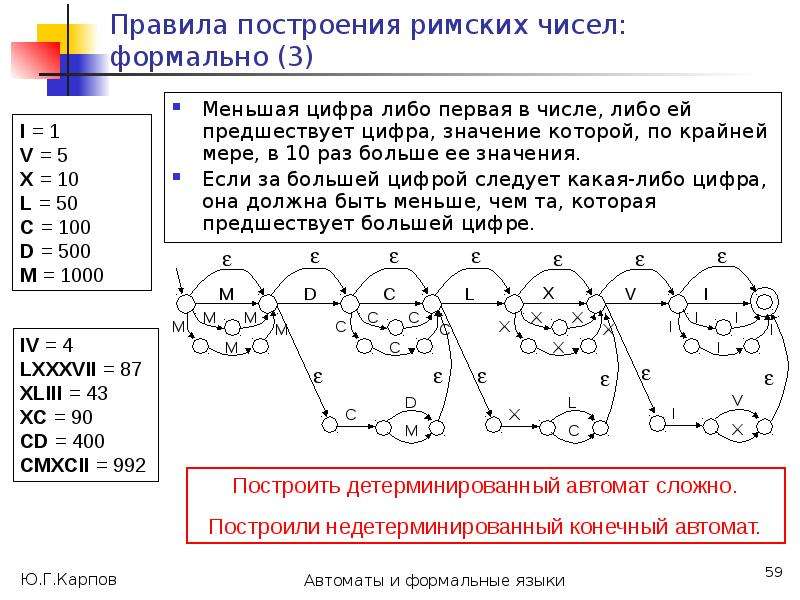
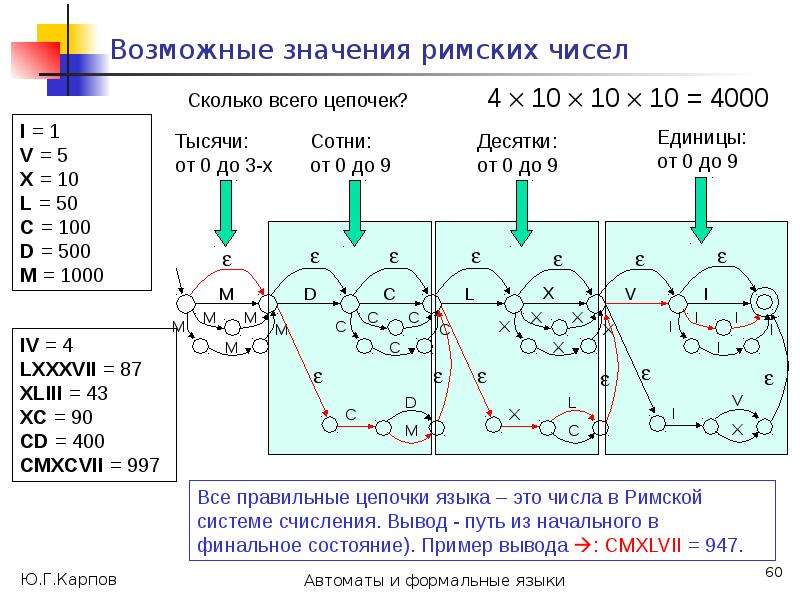
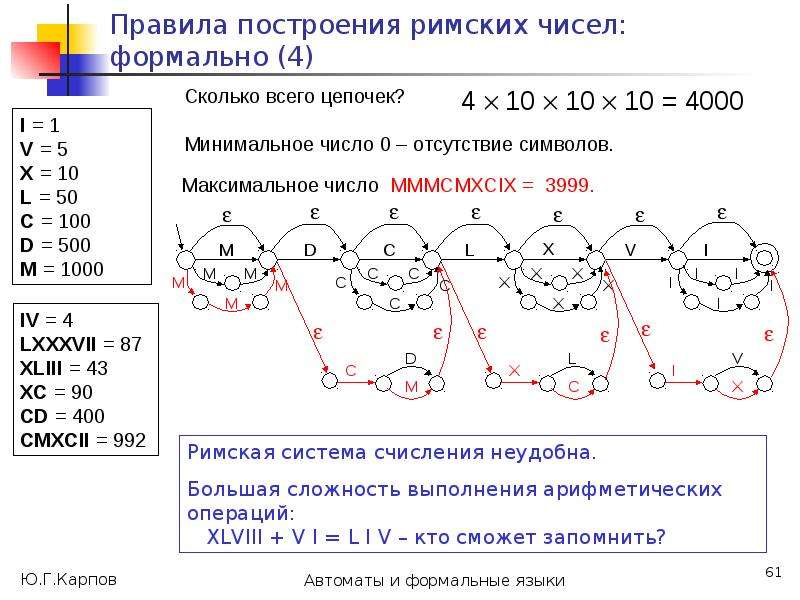
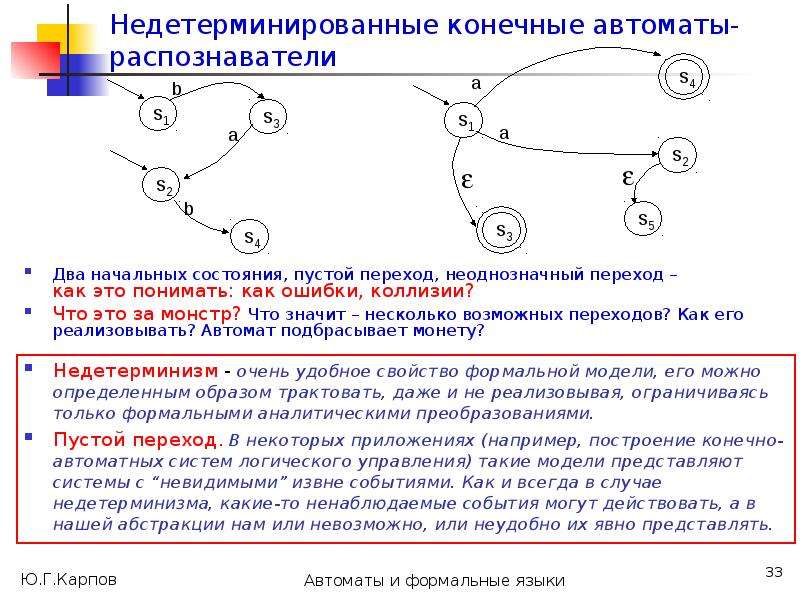
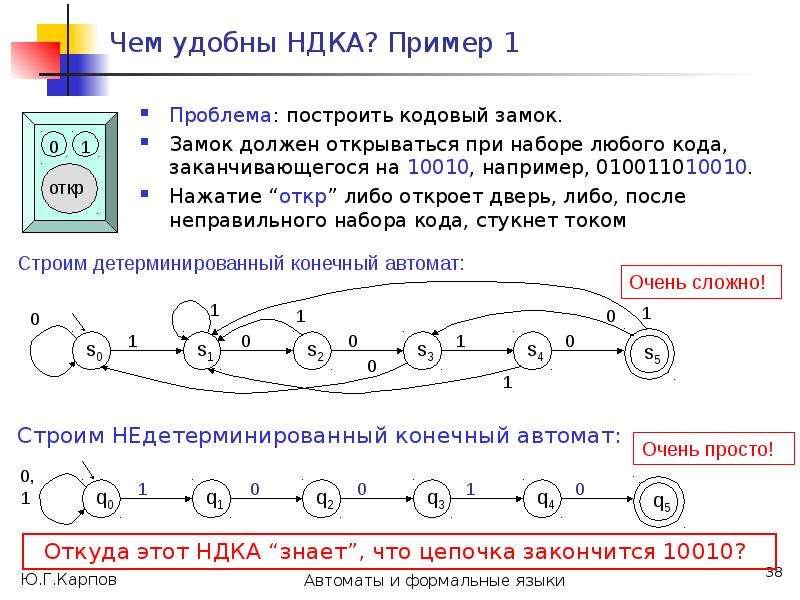
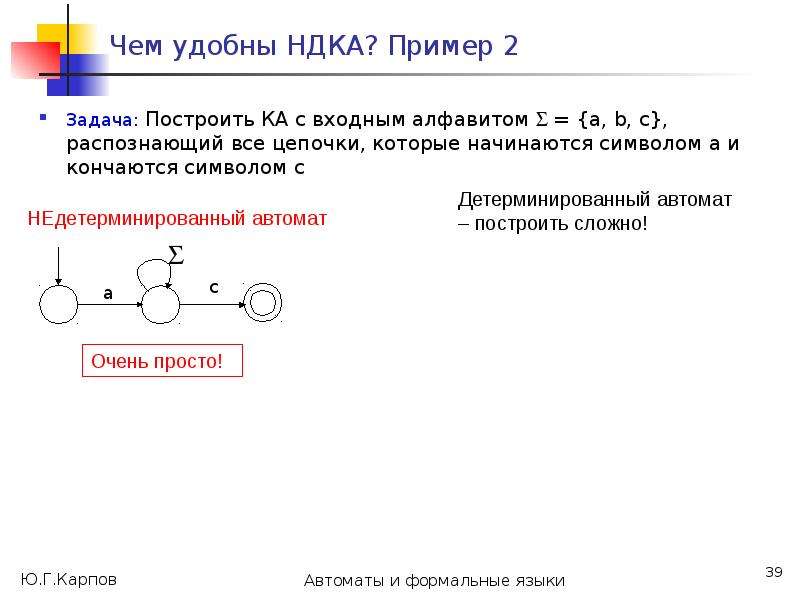
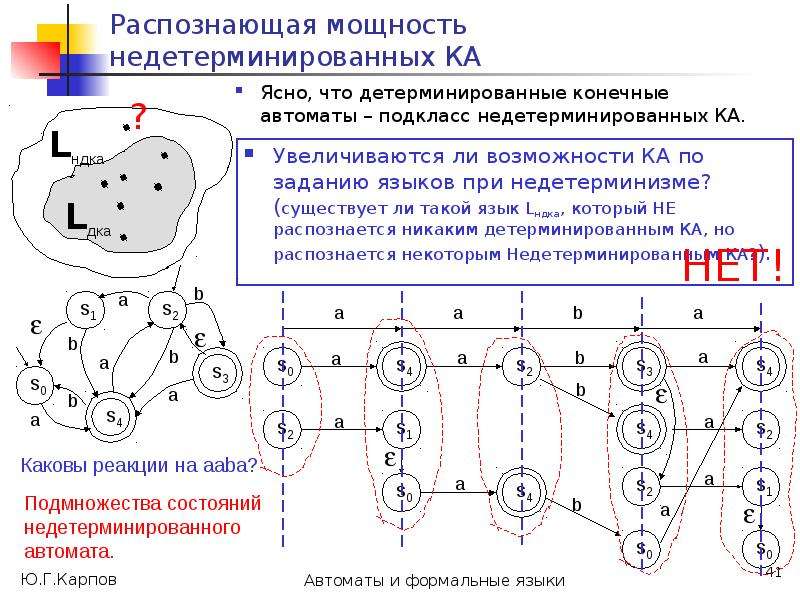
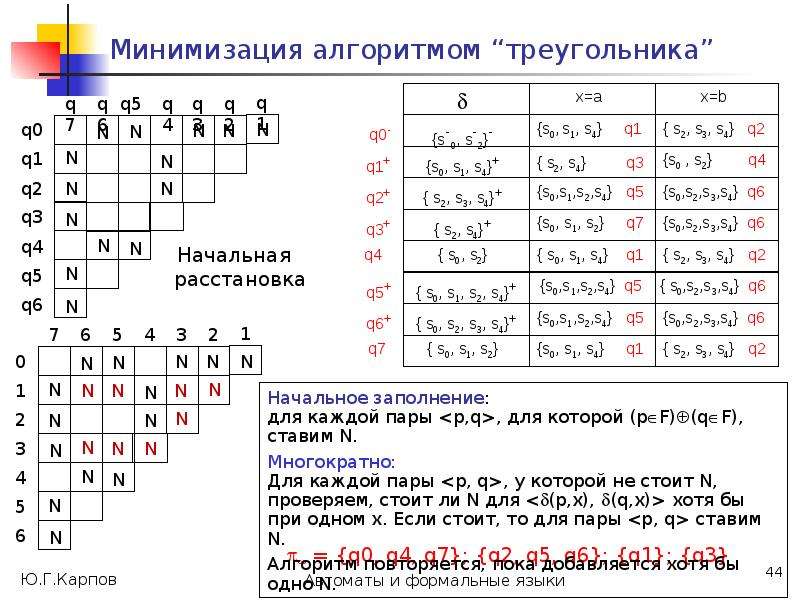
Недетерминированные автоматы: общее понимание Недетерминированные автоматы нельзя рассматривать, как физические устройства, которые читают входные символы, принимают решение, “угадывают”, в какое из состояний перейти, “обладают интуицией”, чтобы выбрать “правильный путь”, откуда-то “зная”, какими будут следующие символы входного слова (как в [1]). Недетерминированный автомат-распознаватель языка – это модель, математическая абстракция, абстрактное порождение мысли, ее бессмысленно реализовывать. С ней можно выполнять некоторые формальные операции: анализ, эквивалентные преобразования. По каждому недетерминированному автомату-распознавателю можно построить эквивалентный ему детерминированный автомат, а такой автомат можно реализовать и программно, и аппаратно.

Заключение Операции над КА-распознавателями: “trimming” – приведение, т.е. выбрасывание недостижимых и некодостижимых состояний в КА; по языку L, распознаваемому заданным КА, построение автомата, распознающего дополнение языка L,т.е. языка * - L; построение синхронной композиции двух КА-распознавателей = построение автомата, распознающего пересечение двух автоматных языков; проверка эквивалентности двух КА-распознавателей; минимизация КА-распознавателя; построение по недетерминированному КА эквивалентного детерминированного КА-распознавателя; построение КА, распознающего объединение и конкатенацию двух автоматных языков, заданных своими распознающими КА.

Заключение (2) Существует простой алгоритм проверки эквивалентности КА. Для такой проверки строится синхронная композиция автоматов. Синхронная композиция автоматов определяет пересечение двух автоматных языков. Конечные автоматы-распознаватели могут быть не минимальными. Алгоритм минимизации КА прост, он похож на алгоритм минимизации автоматов-преобразователей. Недетерминированный КА – это НЕ операционное устройство, которое действует, функционирует, принимая на вход цепочку. Это математическая модель, удобная для задания, для порождения языков. Недетерминизм КА не увеличивает возможностей распознавания языков: для любого недетерминированного КА существует эквивалентный ему детерминированный КА. Автоматные языки замкнуты относительно операций объединения, пересечения, конкатенации и дополнения.

Спасибо за внимание Спасибо за внимание

Эквивалентные автоматы-распознаватели: ПРИМЕРЫ

Эквивалентные автоматы-распознаватели. ПРИМЕР Все три автомата-распознавателя эквивалентны Они распознают один и тот же язык Третий пример показывает, что автомат с бесконечным числом состояний может быть эквивалентным конечному автомату