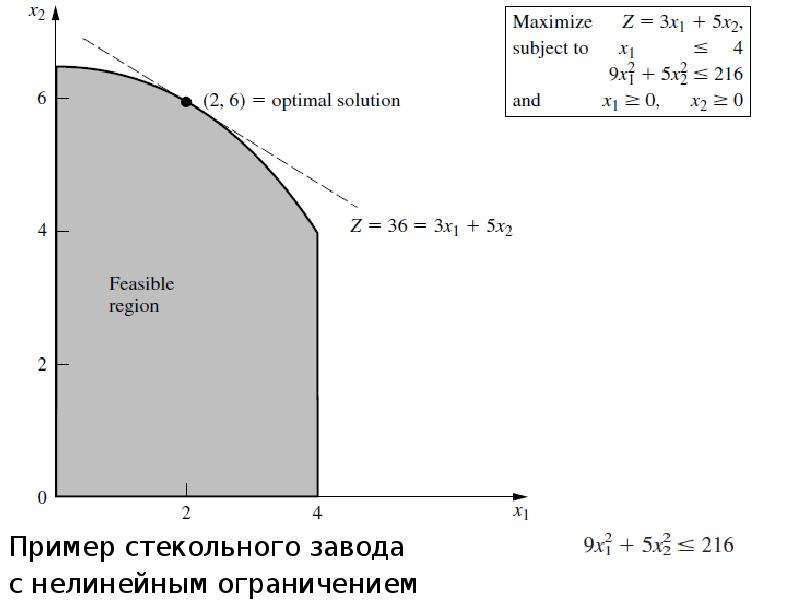
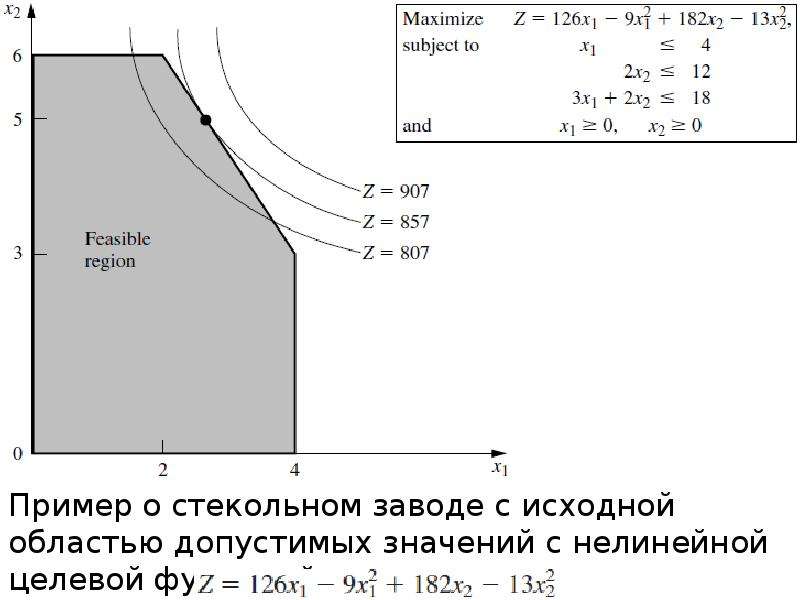
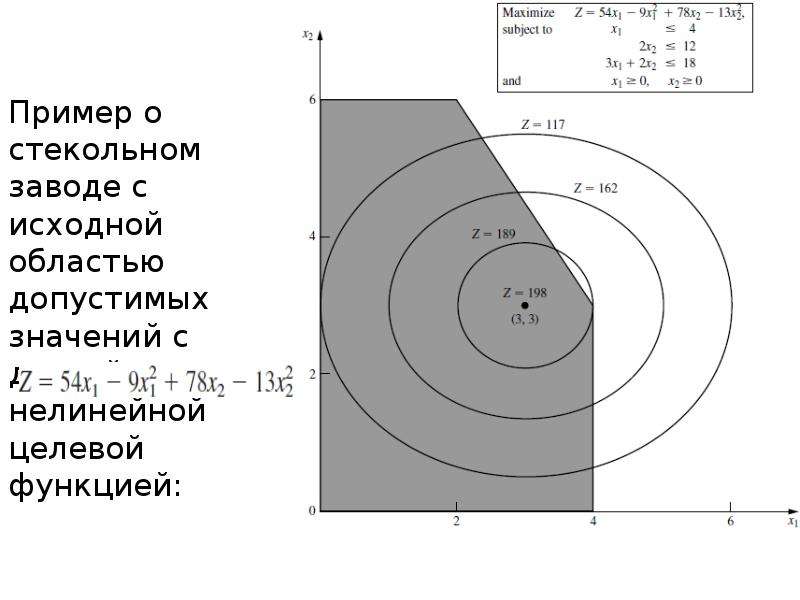
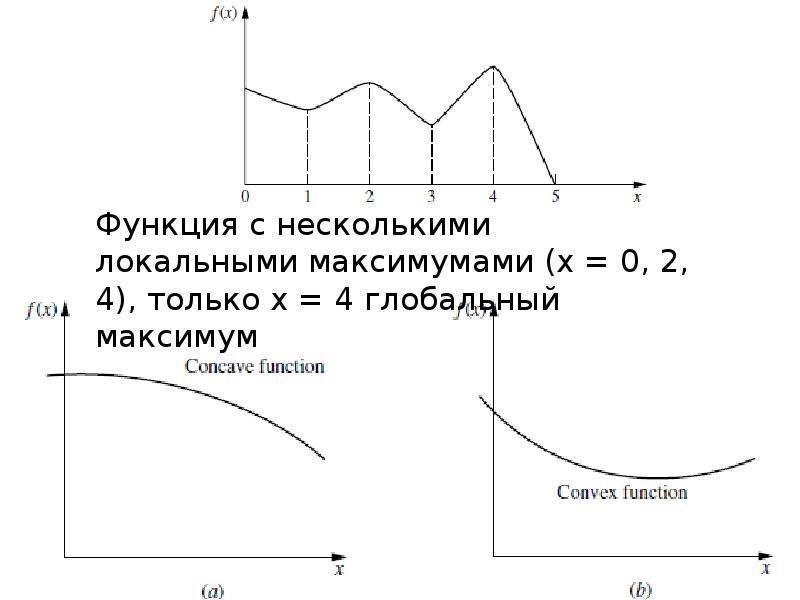
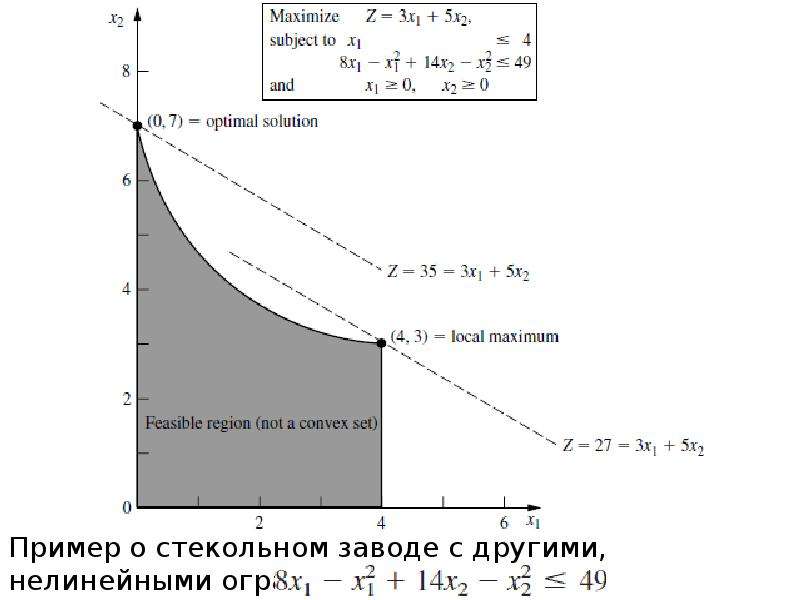
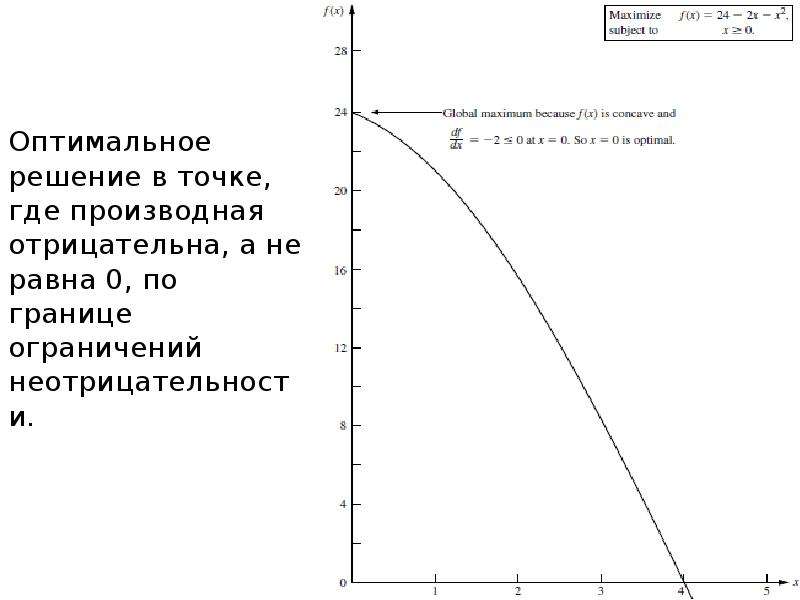
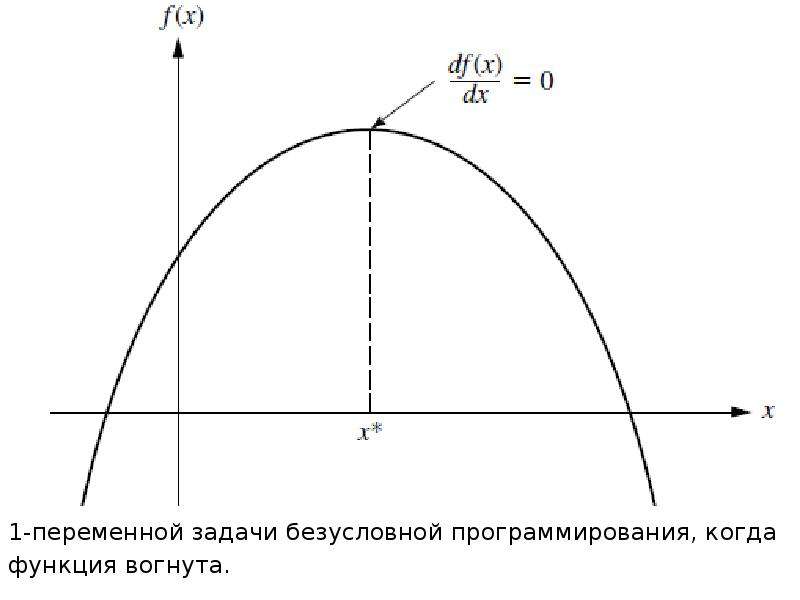
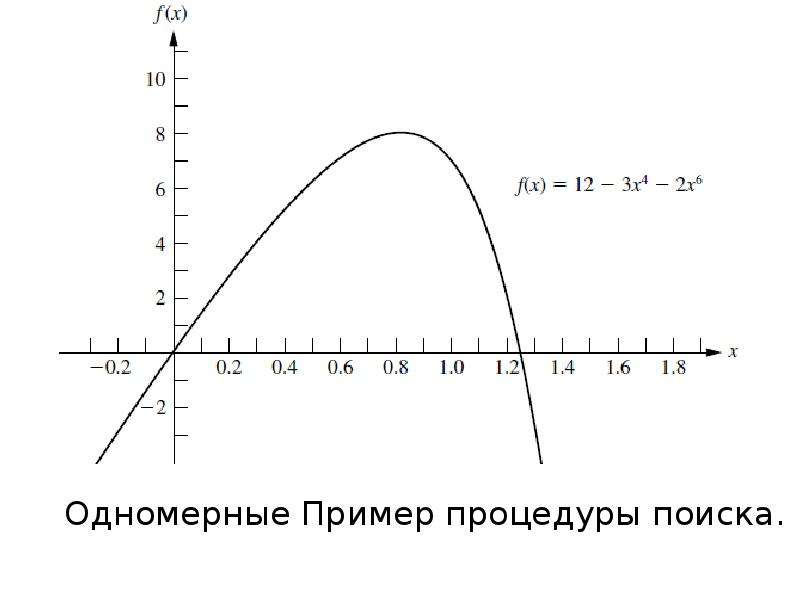
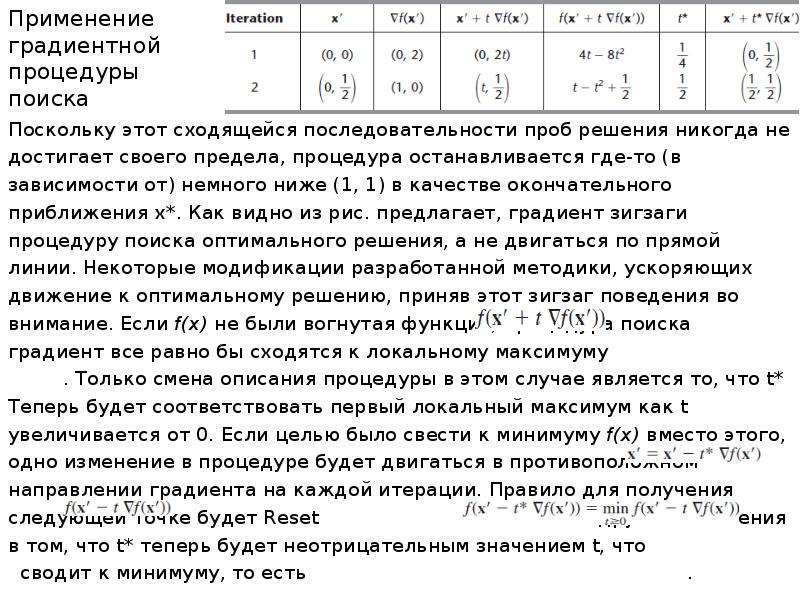
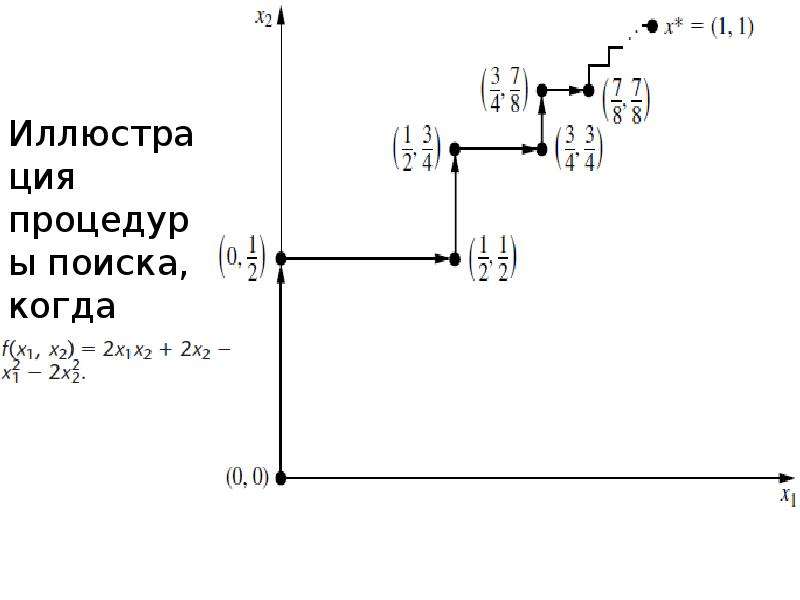
Описание слайда:
Одно из этих приложений возникает двойственность в теории, развитой для нелинейного программирования параллельных теории двойственности в линейном программировании. Для любого ограниченного задачи максимизации (прямая задача), ККТ условия могут быть использованы для определения тесно связана двойственная задача, которая задаче условной минимизации. Переменные в двойственной задачи состоят как из интерфейса множителей Лагранжа (I = 1,2, ..., т) и первичных переменных XJ (J = 1,2, ..., N). Частный случай, когда исходная задача является задачей линейного программирования, переменные XJ выпадают из двойственной задачи, и она становится знакомым двойственной задачи линейного программирования (UI переменных здесь соответствуют Yi переменных). Когда прямая задача выпуклого программирования является проблемой, можно установить связь между основной задачи и двойственной задачи аналогичны линейного программирования. Например, сильным свойством двойственности, в котором говорится, что оптимальная значений целевой функции двух задач совпадают, имеет место и здесь. Значения щ переменных в оптимальное решение для двойной проблема может снова быть интерпретированы как тень цены, то есть, они дают скорость, с которой оптимальное значение целевой функции для прямой задачи может быть увеличена (слегка) увеличение правой стороне соответствующего ограничения. Теория двойственности нелинейного программирования является сложная тема.
Одно из этих приложений возникает двойственность в теории, развитой для нелинейного программирования параллельных теории двойственности в линейном программировании. Для любого ограниченного задачи максимизации (прямая задача), ККТ условия могут быть использованы для определения тесно связана двойственная задача, которая задаче условной минимизации. Переменные в двойственной задачи состоят как из интерфейса множителей Лагранжа (I = 1,2, ..., т) и первичных переменных XJ (J = 1,2, ..., N). Частный случай, когда исходная задача является задачей линейного программирования, переменные XJ выпадают из двойственной задачи, и она становится знакомым двойственной задачи линейного программирования (UI переменных здесь соответствуют Yi переменных). Когда прямая задача выпуклого программирования является проблемой, можно установить связь между основной задачи и двойственной задачи аналогичны линейного программирования. Например, сильным свойством двойственности, в котором говорится, что оптимальная значений целевой функции двух задач совпадают, имеет место и здесь. Значения щ переменных в оптимальное решение для двойной проблема может снова быть интерпретированы как тень цены, то есть, они дают скорость, с которой оптимальное значение целевой функции для прямой задачи может быть увеличена (слегка) увеличение правой стороне соответствующего ограничения. Теория двойственности нелинейного программирования является сложная тема.