🗊Презентация Об алгоритмах на примерах

Общность и эффективность решения задачи Общие решения - менее эффективны. Более узкие решения (одной задачи, например, а не целого класса) - более эффективны Как следствие стало необходимым понятие сложности дискретных алгоритмов и задач, которое позволяет лучше понять причины неэффективности решений, понять, можно ли исключить полный перебор в решении задачи.

Задача об упаковке рюкзака: Множество вещей {Pp | p=(v,w)}Упаковать вещи так, чтобы суммарная ценность V была максимальной при суммарном весе не превоcходящем W. Другие задачи: планирование исполнения множества программ, размещение груза на корабле, и т.д. и т.п. Полный ПЕРЕБОР Сложность = O(n!) Метод ветвей и границ. Известно решение V = k, надо построить решение. Частично построенный вариант можно не испытывать, если он уже хуже оптимального. Класс задач NP – множество всех переборных задач, Класс Р – переборные задачи, разрешимые за полиномиальное время Построить оптимальную упаковку можно полным перебором, а иного, не переборного, алгоритма может и в принципе не существовать. Это и есть труднорешаемая задача.

СВОДИМОСТЬ Переборная задача П1 сводится к переборной задаче П2, если метод решения П1 можно преобразовапть к методу решения П2. Сводимость полиномиальная, если это преобразование можно сделать за полиномиальное время. NP-полные задачи те, к которым полиномиально сводятся любая задача из NP, это класс универсальных в некотором смысле задач. Если бы Р= NP, тогда можно было бы надеяться создать эффективные полиномиальные алгоритмы решения переборных задач. Но к сожалению, это видимо не так и для решения каждой переборной задачи придется разрабатывать свои эффективные алгоритмы решения

Полиномиальная и экспоненциальная сложность Функция f(n) есть O(g(n)), если |f(n)| ≤ c| g(n)|. Полиномиальный (полиномиальной временнόй сложностью) называется алгоритм, сложность которого O(р(n)), где р(n) полином от n. Если алгоритм невозможно так оценить, то он имеет экспоненциальную сложность. Скорость роста n = 10 20 30 40 линейная сложность 0,001 0,002 0,003 0,004 квадратичная сложность 0,001 0,004 0,009 0,016 (n2) показательная функция (экспоненциальная сложность) 2n 0.1 10 Полнопереборные задачи: Найти в графе кратчайшее расстояние между вершинами А и В Раскраска графа. Задан граф G=(V,E), K≤|V|. Существует ли К-раскраска, при которой любые две связанные вершины раскрашиваются в разные цвета?

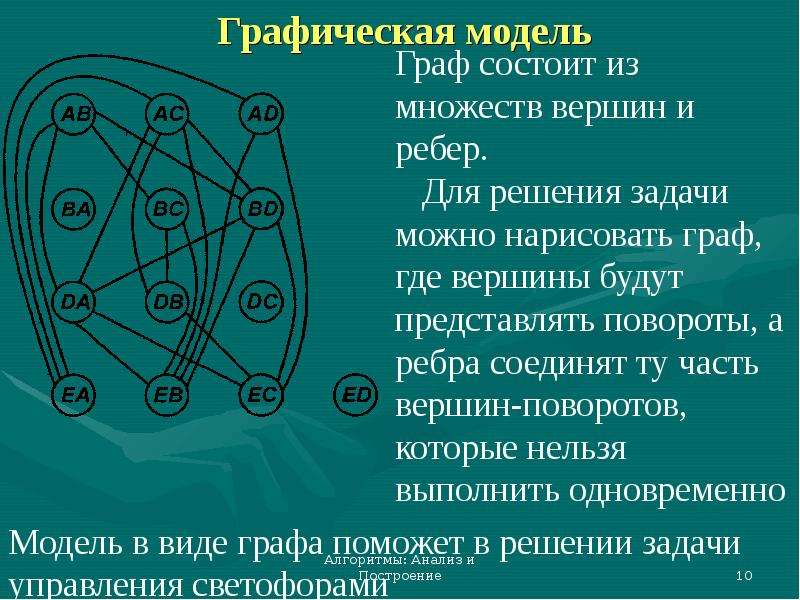
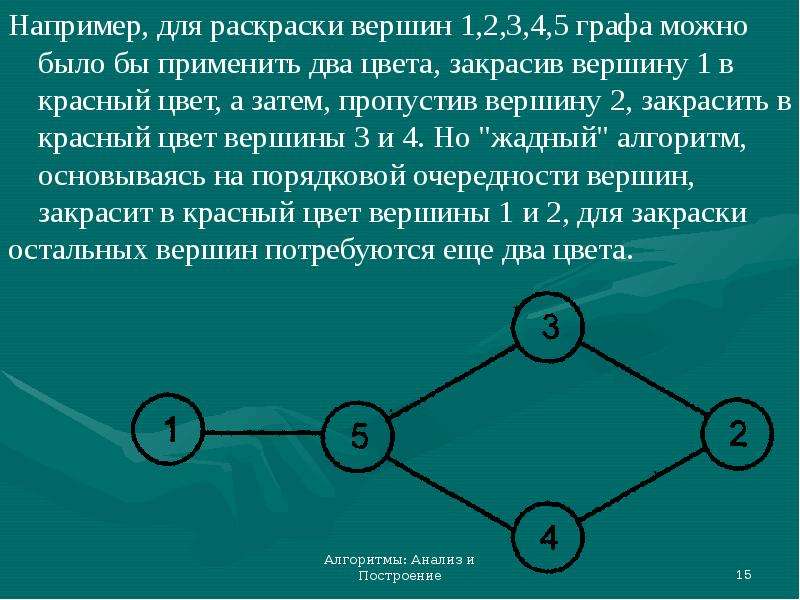
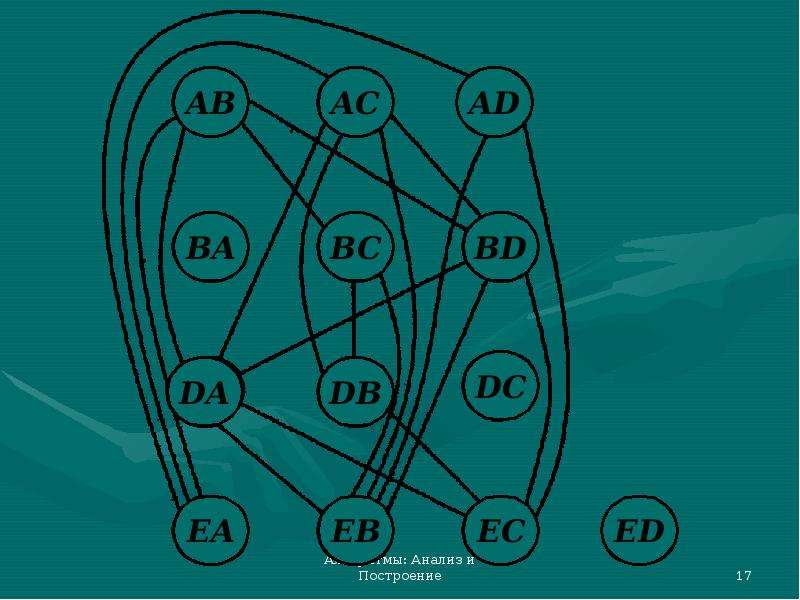
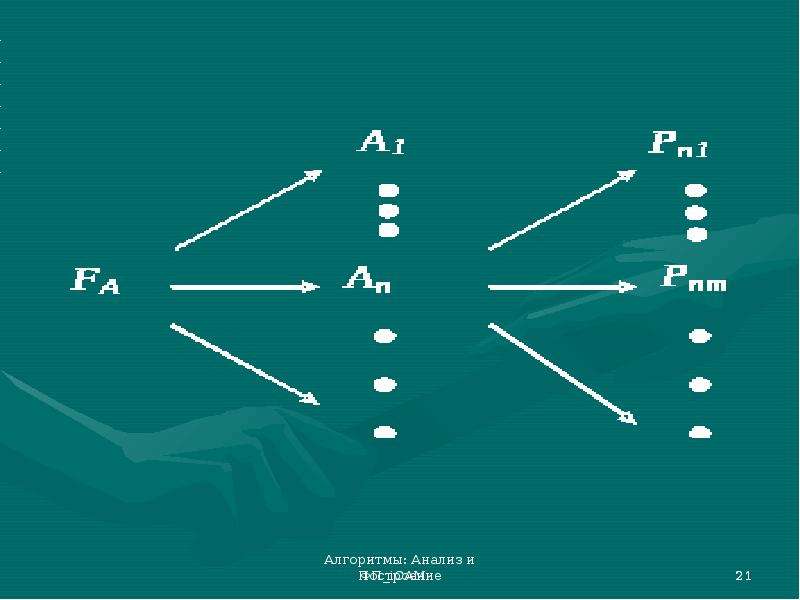
Инварианты цикла (loop invariant) В начале каждой итерации цикла for подмассив А [1..j-1] содержит те же элементы, которые были в нем с самого начала, но расположенные в отсортированном порядке. Инварианты циклов обладают следующими тремя свойствами. Инициализация. Они справедливы перед первой инициализацией цикла. Сохранение. Если они истинны перед очередной итерацией цикла, то остаются истинны и после нее. Завершение. По завершении цикла инварианты позволяют убедиться в правильности алгоритма.

Анализ алгоритма Время работы процедуры Insertion__Sort зависит от набора входных значений: для сортировки тысячи чисел требуется больше времени, чем для сортировки трех чисел. Кроме того, время сортировки может быть разным для последовательностей, состоящих из одного и того же количества элементов, в зависимости от степени упорядоченности этих последовательностей до начала сортировки. В общем случае время работы алгоритма увеличивается с увеличением количества входных данных, поэтому общепринятая практика — представлять время работы программы как функцию, зависящую от количества входных элементов. Понятие размер задачи уточняется для каждой задачи. Это может быть число от числа элементов в массиве, от количества битов для представления входных данных, от количества вершин и дуг графа и т.д.

Время работы алгоритма для того или иного ввода измеряется в количестве элементарных операций, или "шагов", которые необходимо выполнить. Каждый элементарный шаг выполняется за константное время. Время работы алгоритма для того или иного ввода измеряется в количестве элементарных операций, или "шагов", которые необходимо выполнить. Каждый элементарный шаг выполняется за константное время. введем для процедуры Insertion_Sort время выполнения каждой инструкции и количество их повторений. Для каждого j = 2,3,..., n, где n = length [А], обозначим через tj количество проверок условия в цикле while Время работы алгоритма (эффективность алгоритма) — это сумма времён, необходимых для выполнения каждой входящей в его состав исполняемой инструкции. Если выполнение инструкции длится в течение времени сi и она повторяется в алгоритме n раз, то ее вклад в полное время работы алгоритма равно сi n. Чтобы вычислить время работы алгоритма Insertion_Sort (обозначим его через T(n)), нужно просуммировать произведения значений, стоящих в столбцах время и количество раз, в результате чего получим:

Insertion_Sort(A) время количество раз Insertion_Sort(A) время количество раз 1 for j  2 to length[A] c1 n 2 do key  A[j] c2 n — 1 3 - Вставка элемента A[j] в отсортированную последовательность A[1,...,j — 1]. 0 n — 1 4 i  j — 1 с4 n — 1 5 while i > 0 and A[i] > key c5 6 do A[i + 1]  A[i] c6 7 i  i — 1 c7 8 А[i +1]  key c8 n — 1

ПОРЯДОК роста функции Огрубляем оценку роста an2 +bn +c , отбрасывая члены меньших порядков и опуская коэффициент при n2 (это константа) получаем порядок роста n2 . Алгоритм с меньшим порядком роста предпочтительнее, так как при росте n такой полином растет медленнее.

Построение алгоритма методом разделяй и властвуй Рекурсивные алгоритмы. Задача разбивается на подзадачи. Затем эти задачи меньшего размера решаются рекурсивным вызовом разрабатываемой процедуры и так пока размер массива дойдет до единицы, а это уже упорядоченный массив. Соединение двух упорядоченных массивов в один делается процедурой MERGE объединения двух упорядоченных массивов А[p..q] и А[q..n].

Динамическое программирование Динамическое программирование  — способ решения сложных задач путём разбиения их на более простые подзадачи, сложность которых меньше исходной Чтобы решить поставленную задачу, требуется решить подзадачи, после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений.

В общем случае задача решается в три шага - Разбиение задачи на подзадачи меньшего размера. - Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм - Использование полученного решения подзадач для конструирования решения исходной задачи

Пример динамического программирования — алгоритм, позволяющий решить задачу о перемножении цепочки матриц. Пусть имеется последовательность (цепочка), состоящая из n матриц, и нужно вычислить их произведение Пример динамического программирования — алгоритм, позволяющий решить задачу о перемножении цепочки матриц. Пусть имеется последовательность (цепочка), состоящая из n матриц, и нужно вычислить их произведение А1А2 … Аn. Это произведение можно вычислить, используя в качестве подпрограммы стандартный алгоритм умножения пар матриц. Однако сначала нужно расставить скобки, чтобы устранить все неоднозначности в порядке перемножения (зафиксировать порядок перемножения).

(А1(А2(А3А4))) , (А1(А2(А3А4))) , (А1((А2А3) А4)) , ((А1(А2А3)) А4) , (((А1А2) А3) А4) . то способ вычисления их произведения можно полностью определить с помощью скобок разными способами: (А1(А2(А3А4))) (А1((А2А3)А4)) , ((А1(А2А3))А4) , (((А1А2)А3)АА) . Пример динамического программирования — алгоритм, позволяющий решить задачу о перемножении цепочки матриц. Пусть имеется последовательность (цепочка), состоящая из n матриц, и нужно вычислить их произведение А1А2 … Аn. Это произведение можно вычислить, используя в качестве подпрограммы стандартный алгоритм умножения пар матриц. Однако сначала нужно расставить скобки, чтобы устранить все неоднозначности в порядке перемножения (зафиксировать порядок перемножения).

Матричное умножение обладает свойством ас-социативности, поэтому результат не зависит от расстановки скобок. Матричное умножение обладает свойством ас-социативности, поэтому результат не зависит от расстановки скобок. От того как расставлены скобки при умножении последовательности матриц, может сильно зависеть время, затраченное на вычисление произведения. Матрицы А и В можно перемножать, только если они совместимы: количество столбцов матрицы А должно совпадать с количеством строк матрицы В. Если А — это матрица размера р × q, а В - матрица размера q×r, то в результате их перемножения получится матрица С размера р × r.

Время вычисления матрицы С преимущественно определяется количеством произведений скаляров. Это количество равно pqr. Это и есть стоимость умножения матриц Время вычисления матрицы С преимущественно определяется количеством произведений скаляров. Это количество равно pqr. Это и есть стоимость умножения матриц

ПРИМЕР. ПРИМЕР. Перемножаются три матрицы (А1, A2, A3). Предположим, что размеры этих матриц равны 10 х 100, 100 х 5 и 5 х 50 соответственно. Перемножая матрицы в порядке, заданном выражением ((А1 A2) A3), необходимо выполнить 10 *100 *5 = 5 000 скалярных умножений, чтобы найти результат произведения А1, A2 (при этом получится матрица размером 10 х 5), а затем — еще 10 * 5 * 50 = 2 500 скалярных умножений, чтобы умножить эту матрицу на матрицу А3. Всего получается 7 500 скалярных умножений.

Если вычислять результат в порядке, заданном выражением (А1 (A2 A3)), то сначала понадобится выполнить 100 *5 *50 = 25 000 скалярных умножений (при этом будет найдена матрица Если вычислять результат в порядке, заданном выражением (А1 (A2 A3)), то сначала понадобится выполнить 100 *5 *50 = 25 000 скалярных умножений (при этом будет найдена матрица A2 A3 размером 100 х 50), а затем еще 10 *100*50 = 50 000 скалярных умножений, чтобы умножить А1 на эту матрицу. Всего получается 75 000 скалярных умножений. Таким образом, для вычисления результата первым способом понадобится в 10 раз меньше времени. Следует полностью определить порядок умножений в матричном произведении (А1 A2 …, Аn), при котором количество скалярных умножений сведется к минимуму.

Первый этап применения парадигмы динамического программирования — найти оптимальную вспомогательную подструктуру, а затем с ее помощью сконструировать оптимальное решение задачи по оптимальным решениям вспомогательных задач. В рассматриваемой задаче этот этап можно осуществить следующим образом. Первый этап применения парадигмы динамического программирования — найти оптимальную вспомогательную подструктуру, а затем с ее помощью сконструировать оптимальное решение задачи по оптимальным решениям вспомогательных задач. В рассматриваемой задаче этот этап можно осуществить следующим образом.

Обозначим для удобства результат перемножения матриц Ai A(i+1) … Aj через Ai.j, где i≤j. Заметим, что если задача нетривиальна, т.е. i < j, то любой способ расстановки скобок в произведении Ai … Aj разбивает это произведение на произведение матриц Ai..k и A(k+i).j , где к — целое, удовлетворяющее условию i≤ к < j. Таким образом, при некотором k сначала вычисляются матрицы, а затем они умножаются друг на друга, в результате чего получается произведение Ai..j. Стоимость, соответствующая этому способу расстановки скобок, равна сумме стоимости вычисления матрицы Ai,k , стоимости вычисления матрицы Ak+i..j и стоимости вычисления их произведения. Обозначим для удобства результат перемножения матриц Ai A(i+1) … Aj через Ai.j, где i≤j. Заметим, что если задача нетривиальна, т.е. i < j, то любой способ расстановки скобок в произведении Ai … Aj разбивает это произведение на произведение матриц Ai..k и A(k+i).j , где к — целое, удовлетворяющее условию i≤ к < j. Таким образом, при некотором k сначала вычисляются матрицы, а затем они умножаются друг на друга, в результате чего получается произведение Ai..j. Стоимость, соответствующая этому способу расстановки скобок, равна сумме стоимости вычисления матрицы Ai,k , стоимости вычисления матрицы Ak+i..j и стоимости вычисления их произведения. рассматриваемой задаче этот этап можно осуществить следующим образом.

Предположим, что в результате оптимальной расстановки скобок последовательность Ai … Aj разбивается на подпоследовательности Ai,k , и Ak+i..j Тогда расстановка скобок в "префиксной" подпоследовательности Ai,k тоже должна быть оптимальной. Иначе, если бы существовал более экономный способ расстановки скобок в последовательности Ai,k, то его применение позволило бы перемножить матрицы Ai … Aj еще эффективнее, что противоречит предположению об оптимальности первоначальной расстановки скобок. Аналогично можно прийти к выводу, что расстановка скобок в подпоследовательности матриц A(k+i).j, возникающей в результате оптимальной расстановки скобок в последовательности A(k+i).j, также должна быть оптимальной. Предположим, что в результате оптимальной расстановки скобок последовательность Ai … Aj разбивается на подпоследовательности Ai,k , и Ak+i..j Тогда расстановка скобок в "префиксной" подпоследовательности Ai,k тоже должна быть оптимальной. Иначе, если бы существовал более экономный способ расстановки скобок в последовательности Ai,k, то его применение позволило бы перемножить матрицы Ai … Aj еще эффективнее, что противоречит предположению об оптимальности первоначальной расстановки скобок. Аналогично можно прийти к выводу, что расстановка скобок в подпоследовательности матриц A(k+i).j, возникающей в результате оптимальной расстановки скобок в последовательности A(k+i).j, также должна быть оптимальной.

Для решения любой нетривиальной задачи об оптимальном произведении последовательности матриц всю последовательность необходимо разбить на подпоследовательности и при этом каждое оптимальное решение содержит в себе оптимальные решения подзадач. Другими словами, решение полной задачи об оптимальном перемножении последовательности матриц можно построить путем разбиения этой задачи на две подзадачи — оптимальную расстановку скобок в подпоследовательно- стях AiAi+1... Ak и Ak+iAk+2 • • -Aj. После этого находятся оптимальные решения подзадач, из которых затем составляется оптимальное решение полной задачи. Необходимо убедиться, что при поиске способа перемножения матриц учитываются все возможные разбиения — только в этом случае можно быть уверенным, что найденное решение будет глобально оптимальным. Для решения любой нетривиальной задачи об оптимальном произведении последовательности матриц всю последовательность необходимо разбить на подпоследовательности и при этом каждое оптимальное решение содержит в себе оптимальные решения подзадач. Другими словами, решение полной задачи об оптимальном перемножении последовательности матриц можно построить путем разбиения этой задачи на две подзадачи — оптимальную расстановку скобок в подпоследовательно- стях AiAi+1... Ak и Ak+iAk+2 • • -Aj. После этого находятся оптимальные решения подзадач, из которых затем составляется оптимальное решение полной задачи. Необходимо убедиться, что при поиске способа перемножения матриц учитываются все возможные разбиения — только в этом случае можно быть уверенным, что найденное решение будет глобально оптимальным.

Организация больших массивов Алгоритмы размещения и поиска данных. Определить алгоритмы вычисления функций РАЗМЕСТИТЬ, НАЙТИ и УДАЛИТЬ элемент. Массив помещается в оперативной памяти . Прямая адресация, как в массиве программы: Ключ элемента – целочисленный номер. Лексикографическое упорядочивание. Ключ элемента – текст имени элемента

Hash-таблицы Массив большой и, например, не помещается весь в оперативной памяти, но в каждый момент времени обрабатывается ограниченное количество элементов. В этом случае используются hash- функции.

Какой должна быть хорошая hash-функция?