🗊Презентация Построение асимптотических ЛАЧХ

Построение асимптотических ЛАЧХ

Асимптотическая АЛАЧХ Пусть ПФ , для примера возьмем Перепишем ПФ так, чтобы привести все множители вида (s+a) к (s*b+1), в нашем случае . Множители s в минус первой степени являются сопрягающими частотами (для нашего примера эти частоты: 1 (в числителе ПФ), 10 и 100 (в знаменателе ПФ).

Асимптотическая АЛАЧХ Построение АЛАЧХ начинается, исходя из следующих соображений: При отсутствии интеграторов/дифференциаторов АЛАЧХ до сопрягающих частот представляет из себя прямую с нулевым наклоном, которая расположена на высоте 20 lg(k), где k - множитель ПФ. В нашем случае k=0.1 и высота прямой равна 20lg(0.1)=-20. Если интегратор или дифференциатор есть, то АЛАЧХ до сопрягающих частот представляет из себя прямую с наклоном (a-b)*20 Дб/дек, где а – кол-во дифференциаторов, а b – количество интеграторов, причем эта прямая пересекает значение 20lg(k) на частоте 1. Для ПФ АЛАЧХ представляет из себя прямую с наклоном -20Дб/дек, которая на частоте 1 проходит через точку 20lg(5)≈14. При пересечении сопрягающей частоты АЛАЧХ меняет свой наклон на +20Дб/дек или -20Дб/дек, в зависимости от принадлежности частоты к нулям или к полюсам ПФ соответственно. Для нашего примера, при проходе через частоту 1 наклон прямой изменяется на +20 Дб/дек, а при проходе через частоты 10 и 100 изменяется на -20/дек.

Алгоритм 1. Привести к виду чтобы привести все множители вида (s+a) к (s*b+1) 2. Определить сопрягающие частоты 3. Есть ли в ПФ интеграторы/дифференциаторы? 4. При пересечении сопрягающей частоты АЛАЧХ меняет свой наклон на +20Дб/дек или -20Дб/дек, в зависимости от принадлежности частоты к нулям или к полюсам ПФ соответственно. Полюс (корень числителя), тогда+20Дб/дек к наклону АЛАЧХ Ноль (корень знаменателя), тогда -20Дб/дек к наклону АЛАЧХ

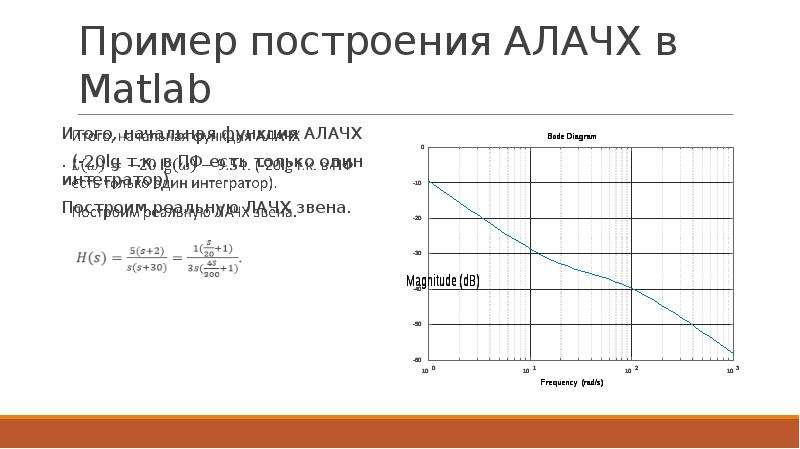
Пример построения АЛАЧХ в Matlab Таким образом, последовательность команд для построения данной АЛАЧХ поверх ЛАЧХ вышла следующей : >> hold on >> loglog([10^-2 10^0],[-20 -20],'r') >> loglog([10^0 10^1],[-20 0],'r') >> loglog([10^1 10^2],[0 0],'r') >> loglog([10^2 10^4],[0 -40],'r')

Рассмотрим пример с интегратором Пусть . Приведем все множители вида (s+a) к (s*b+1): . Найдем сопрягающие частоты: Частоты, принадлежащие к нулям: =20. Частоты, принадлежащие к полюсам: =300/4=75. Т.к. имеем интегратор, надо найти точку пересечения частоты : 20lg(1/3)=-9.54

Пример построения АЛАЧХ в Matlab Итого, начальная функция АЛАЧХ . (-20lg т.к. в ПФ есть только один интегратор). Построим реальную ЛАЧХ звена.

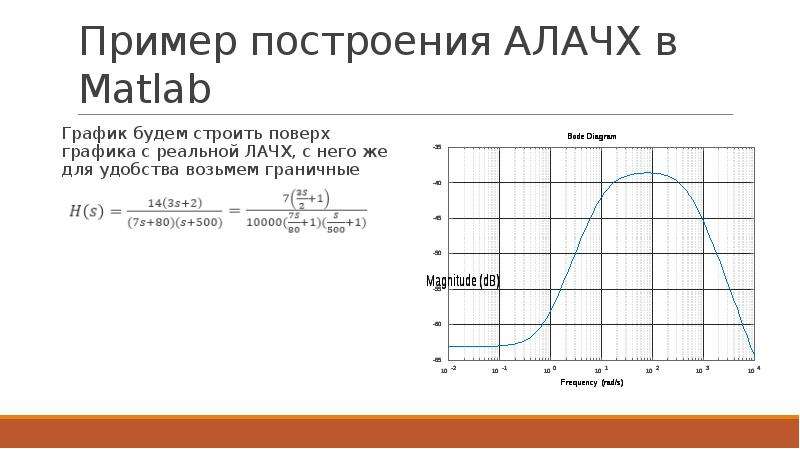
Пример построения АЛАЧХ в Matlab Для удобства будем строить АЛАЧХ поверх реальной ЛАЧХ. Таким образом, для построения АЛАЧХ нам потребуются следующая последовательность команд: >> hold on >> p0=9.54 >> loglog([10^0 20], [-20*log10(10^0)-p0 -20*log10(20)-p0 ], 'r') >> p1= -20*log10(20)-p0 >> loglog([20 75], [p1 p1], 'r') >> p2= -20*log10(75)-p1 >> loglog([75 10^3], [-20*log10(75)-p2 -20*log10(10^3)-p2], 'r')

Итоговая АЛАЧХ

Еще один пример без интегратора Сопрягающие частоты для нулей: 2/3, для полюсов: 80/7, 500. Начальный наклон прямой = 0 Дб/дек. Начальная высота прямой = 20lg(7/10000) = -63

Пример построения АЛАЧХ в Matlab График будем строить поверх графика с реальной ЛАЧХ, с него же для удобства возьмем граничные частоты.

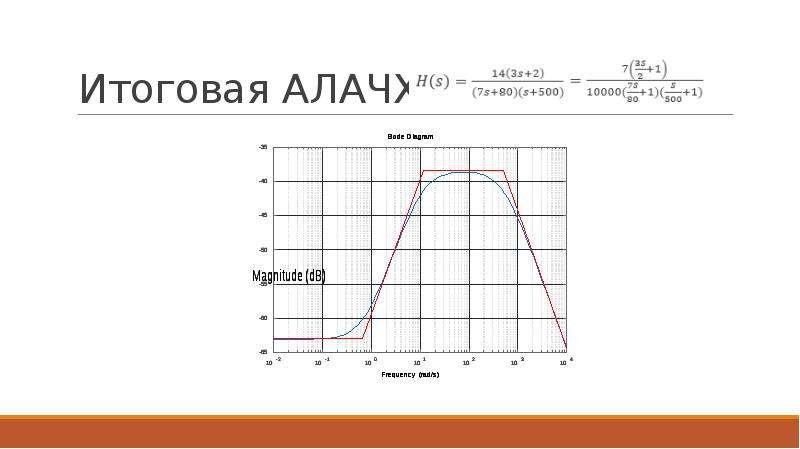
Последовательность команд: >> t8=tf([14*3 14*2],[7 7*500+80 500*80]) >> ltiview(t8) %Строим ЛАЧХ и выводим его в отдельный график >> hold on >> p1=-63 %Установившееся значение >> loglog([10^-2 2/3],[p1 p1],'r') %Линия без наклона >> p2=20*log10(2/3)-p1 %Расчёт поправки >> loglog([2/3 80/7],[20*log10(2/3)-p2 20*log10(80/7)-p2],'r') %Наклон +20 >> p3=20*log10(80/7)-p2 %Установившееся значение >> loglog([80/7 500],[p3 p3],'r') %Без наклона >> p4=-20*log10(500)-p3 %Расчёт поправки >> loglog([500 10^4],[-20*log10(500)-p4 -20*log10(10^4)-p4],'r') %Наклон -20

Итоговая АЛАЧХ