Программирование на языке MATLAB. Графические возможности MATLAB

Нажмите для полного просмотра!

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №2

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №3

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №4

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №5

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №6

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №7

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №8

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №9

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №10

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №11

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №12

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №13

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №14

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №15

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №16

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №17

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №18

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №19

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №20

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №21

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №22

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №23

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №24

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №25

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №26

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №27

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №28

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №29

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №30

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №31

Программирование на языке MATLAB. Графические возможности MATLAB, слайд №32

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Программирование на языке MATLAB. Графические возможности MATLAB. Доклад-сообщение содержит 32 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Слайд 2

Описание слайда:

Вопросы для изучения 4.23 Двумерные и трехмерные графики. 4.24 Редактирование графиков 4.25 Графики в полярных координатах 4.26 ???

Слайд 3

Описание слайда:

4.23 Двумерные и трехмерные графики 4.23 Двумерные и трехмерные графики MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое. Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Основной функцией, обеспечивающей построение графиков на экране дисплея, является функция plot. Общая форма обращения к ней такова: plot(x1, y1, s1, x2, y2, s2,...) где x1, y1 - заданные векторы, элементами которых являются массивы значений аргумента (х1) и функции (y1), отвечающие первой кривой графика; x2, y2 - массивы значений аргумента и функции второй кривой и т.д. При этом предполагается, что значения аргумента откладываются вдоль горизонтальной оси графика, а значения функции - вдоль вертикальной оси.

Слайд 4

Описание слайда:

Переменные s1, s2,... являются символьными (их указание не является обязательным). Любая из них может содержать до трех специальных символов, определяющих соответственно: Переменные s1, s2,... являются символьными (их указание не является обязательным). Любая из них может содержать до трех специальных символов, определяющих соответственно: а) тип линии, которая соединяет отдельные точки графика; б) тип точки графика; в) цвет линии. Если переменные s не указаны, то тип линии по умолчанию - отрезок прямой, тип точки - пиксел, а цвет устанавливается в такой очередности: - синий, зеленый, красный, голубой, фиолетовый, желтый, черный и белый - в зависимости от того, какая по очереди линия выводится на график. Например, обращение вида plot(x1,y1,x2,y2,...) приведет к построению графика, в котором первая кривая будет линией из отрезков прямых синего цвета, вторая кривая - такого же типа зеленой линией и т.д. Наиболее простыми частными случаями являются комманды: - plot (X, Y) служит для построения графика функций одной переменной. - plot(X, Y, S) аналогична команде plot(X, Y), но тип линии графика можно задавать с помощью строковой константы S.

Слайд 5

Описание слайда:

Слайд 6

Описание слайда:

Пример. Пусть нужно вывести график функции y = 3sin(x +π /3) на промежутке от -3π до +3π с шагом π /100. Пример. Пусть нужно вывести график функции y = 3sin(x +π /3) на промежутке от -3π до +3π с шагом π /100. 1) сформировать массив значений аргумента х: x = -3*pi : pi/100 : 3*pi, 2) вычислить массив соответствующих значений функции: y = 3*sin(x+pi/3) 3) построить график зависимости y(х). Последовательность операций в командном окне: » x = -3*pi:pi/100:3*pi; » y = 3*sin(x+pi/3); » plot(x,y) В результате на экране появится окно с графиком (см. рис. 4.71).

Слайд 7

Описание слайда:

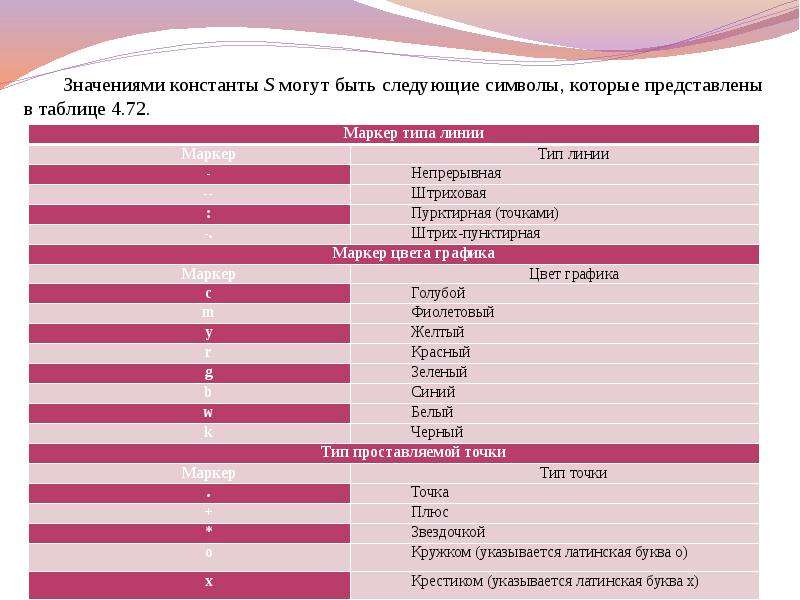
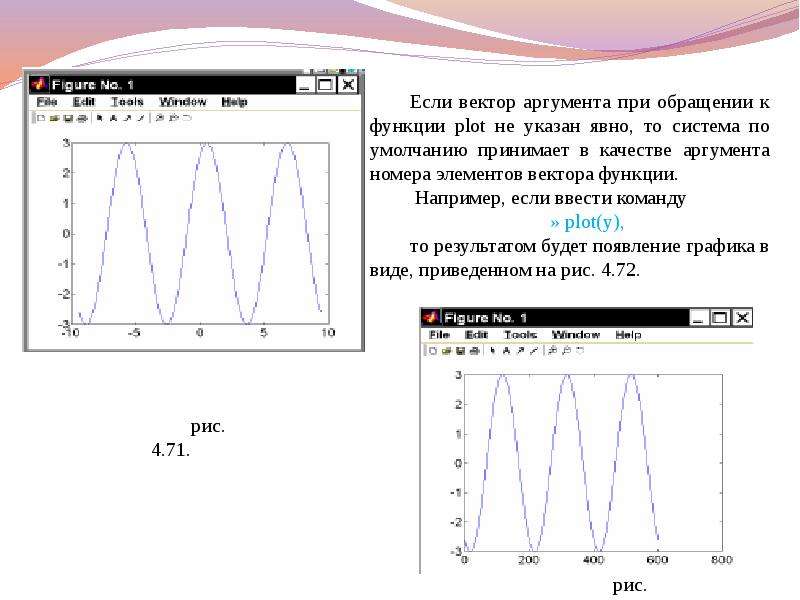
Если вектор аргумента при обращении к функции plot не указан явно, то система по умолчанию принимает в качестве аргумента номера элементов вектора функции. Если вектор аргумента при обращении к функции plot не указан явно, то система по умолчанию принимает в качестве аргумента номера элементов вектора функции. Например, если ввести команду » plot(y), то результатом будет появление графика в виде, приведенном на рис. 4.72.

Слайд 8

Описание слайда:

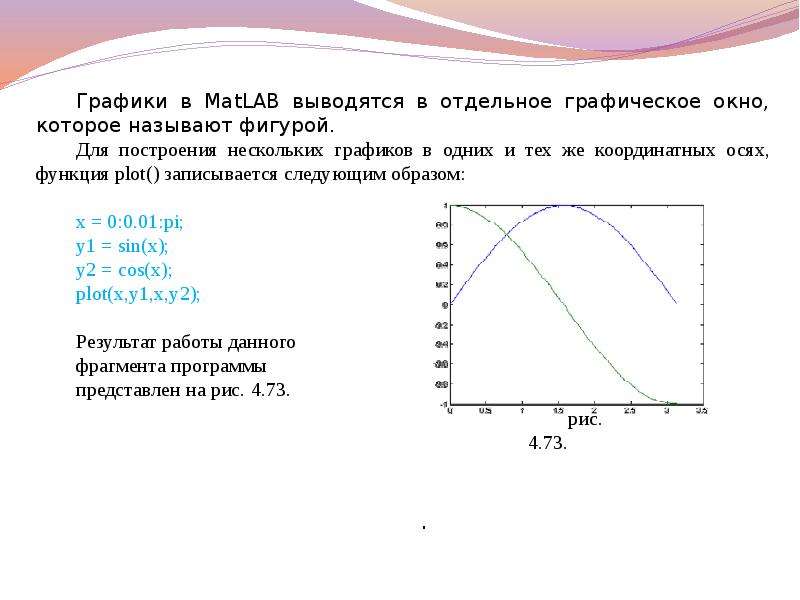
Графики в MatLAB выводятся в отдельное графическое окно, которое называют фигурой. Графики в MatLAB выводятся в отдельное графическое окно, которое называют фигурой. Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом: x = 0:0.01:pi; y1 = sin(x); y2 = cos(x); plot(x,y1,x,y2); Результат работы данного фрагмента программы представлен на рис. 4.73. .

Слайд 9

Описание слайда:

Можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом: Можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом: x1 = 0:0.01:2*pi; y1 = sin(x1); x2 = 0:0.01:pi; y2 = cos(x2); plot(x1, y1); % рисование первого графика figure; % создание 2-го графического окна plot(x2, y2); % рисование 2-го графика во 2-м окне Функция figure, используемая в данной программе, создает новое графическое окно и делает его активным. Функция plot(), вызываемая сразу после функции figure, отобразит график в текущем активном графическом окне. В результате на экране будут показаны два окна с двумя графиками.

Слайд 10

Описание слайда:

Повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. Повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. Для того, чтобы на экране всегда отображалось два окна с нужными графиками при вызове функции figure необходимо в качестве аргумента указывать номер графического окна, которое необходимо создать или сделать активным, если оно уже создано. x1 = 0:0.01:2*pi; y1 = sin(x1); x2 = 0:0.01:pi; 21 y2 = cos(x2); figure(1); %создание окна с номером 1 plot(x1, y1); % рисование первого графика figure(2); % создание графического окна с номером 2 plot(x2, y2); % рисование 2-го графика во 2-м окне

Слайд 11

Описание слайда:

В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис: В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис: subplot(, , ) Пример отображения двух графиков друг под другом вышеприведенных функций синуса и косинуса. x1 = 0:0.01:2*pi; y1 = sin(x1); x2 = 0:0.01:pi; y2 = cos(x2); figure(1); subplot(2,1,1); % делим окно на 2 строки и один столбец, % указываем первое подокно plot(x1,y1); % отображение первого графика subplot(2,1,2); % делим окно на 2 строки и один столбец % указываем второе подокно plot(x2,y2); % отображение второго графика

Слайд 12

Описание слайда:

Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Для этого используется параметр position в функции subplot(): subplot(‘position’, [left bottom width height]); где left – смещение от левой стороны окна; bottom – смещение от нижней стороны окна; width, height – ширина и высота графика в окне. Все эти переменные изменяются в пределах от 0 до 1. Пример программы отображения графика функции синуса в центре графического окна. x1 = 0:0.01:2*pi; y1 = sin(x1); subplot(‘position’, [0.33 0.33 0.33 0.33]); plot(x1,y1); В данном примере функция subplot() смещает график на треть от левой и нижней границ окна и рисует график с шириной и высотой в треть графического окна. Таким образом, используя параметр position можно произвольно размещать графические элементы в плоскости окна.

Слайд 13

Описание слайда:

Для управления созданным окном графика используется команда set Для управления созданным окном графика используется команда set set(object name, 'Property name1',' Property value1', …); где object name – имя управляемого объекта; 'Property name1' – строковая константа содержащая название изменяемого свойства; ' Property value1' – строковая константа содержащая значение изменяемого свойства. Пример: set(figure(1), 'Name','Primer postroeniya grafikov','NumberTitle','on'); в заголовок окна графика figure(1) выводится Figure 1: Primer postroeniya grafikov

Слайд 14

Описание слайда:

Отображение трехмерных графиков Отображение трехмерных графиков MatLab обладает рядом инструментов для визуализации графиков в трехмерном пространстве. Для визуализации графика в трехмерных координатных осях, используется функция plot3(X,Y,Z); где в качестве первых двух аргументов принимает матрицы с координатами точек по осям Ox и Oy соответственно, а в качестве третьего аргумента передается матрица значений точек по оси Oz.

Слайд 15

Описание слайда:

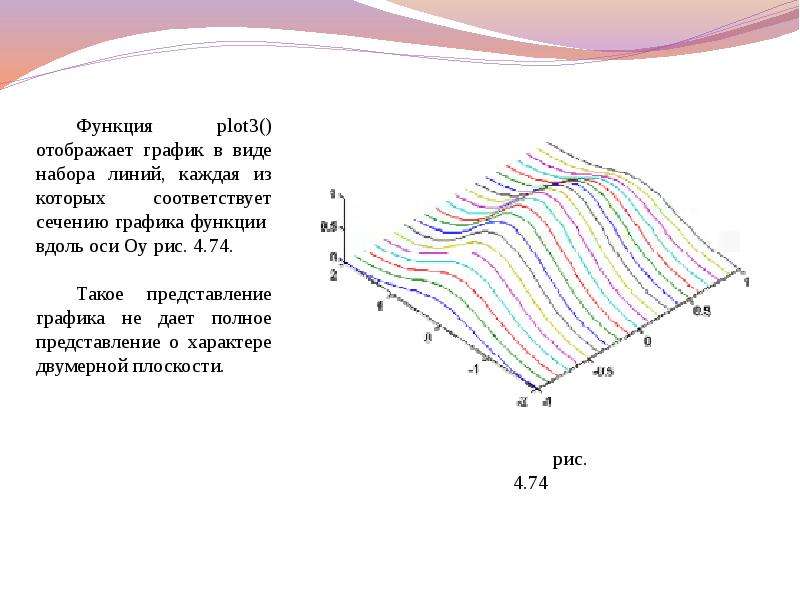
Функция plot3() отображает график в виде набора линий, каждая из которых соответствует сечению графика функции вдоль оси Oy рис. 4.74. Такое представление графика не дает полное представление о характере двумерной плоскости.

Слайд 16

Описание слайда:

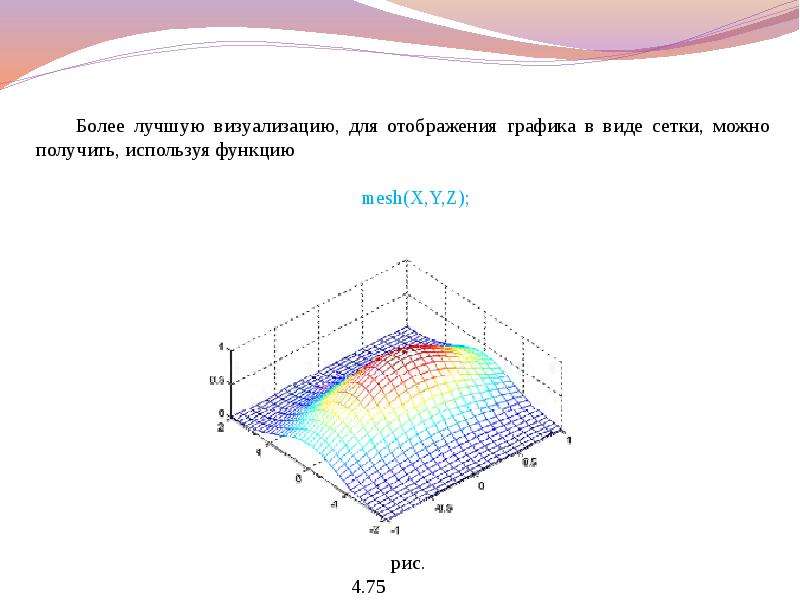
Более лучшую визуализацию, для отображения графика в виде сетки, можно получить, используя функцию mesh(X,Y,Z);

Слайд 17

Описание слайда:

Благодаря использованию функции mesh() получается график, образованный интерполяцией точек массивов X, Y и Z линиями по осям Ox и Oy. Кроме того, цветом указывается уровень точки по оси Oz: от самого малого значения (синего) до самого большого (красного) и производится удаление «невидимых» линий. Это позволяет лучше визуально оценивать структуру трехмерного графика по сравнению с функцией plot3(). Для управления прозрачностью графика используют команду hidden: - hidden off – прозрачность включена; - hidden on– прозрачность выключена.

Слайд 18

Описание слайда:

В системе MatLab предусмотрена функция визуализации непрерывной поверхности в трехмерных осях (рис. 4.76). В системе MatLab предусмотрена функция визуализации непрерывной поверхности в трехмерных осях (рис. 4.76). surf(X,Y,Z); Функция surf строит каркасную поверхность графика функции и заливает каждую клетку поверхности определенным цветом, зависящим от значения функции в точках, соответствующих углам клетки. В переделах каждой клетки цвет постоянный.

Слайд 19

Описание слайда:

Функция surf() может использоваться в режимах: - команда shading flat позволяет убрать каркасные линии. - для получения поверхности, плавно залитой цветом, зависящим от значения функции, предназначена команда shading interp (рис. 4.77). вернуться к начальному виду поверхности можно с помощью команды shading faceted. Возможно также формирование графика, содержащего линии уровня функции, т.е. линии постоянства значений функции на плоскост). Для этого вместо команд mesh или surf надо использовать команды meshc или surfc соответственно.

Слайд 20

Описание слайда:

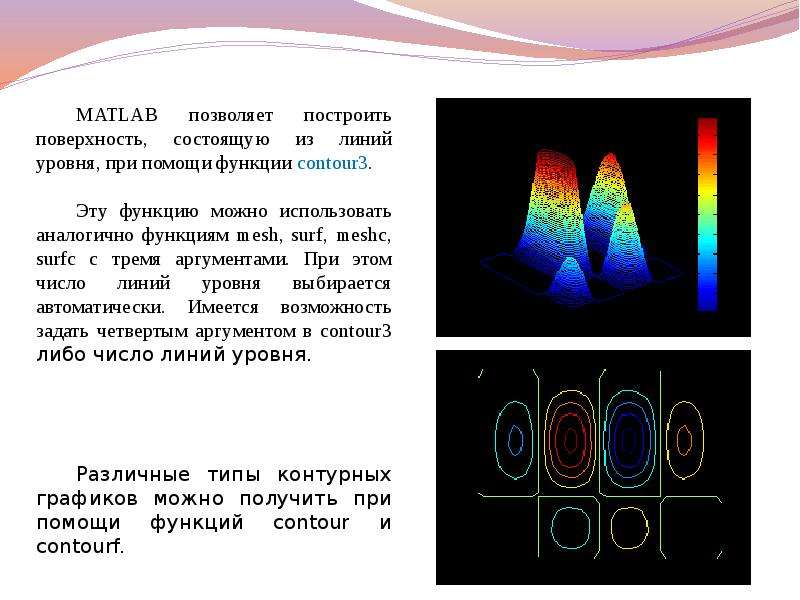
MATLAB позволяет построить поверхность, состоящую из линий уровня, при помощи функции contour3. Эту функцию можно использовать аналогично функциям mesh, surf, meshc, surfc с тремя аргументами. При этом число линий уровня выбирается автоматически. Имеется возможность задать четвертым аргументом в contour3 либо число линий уровня. Различные типы контурных графиков можно получить при помощи функций contour и contourf.

Слайд 21

Описание слайда:

Также существует возможность менять цветовую карту отображения графика с помощью функции Также существует возможность менять цветовую карту отображения графика с помощью функции colormap( ); Например, карта с именем hot, используемая по умолчанию может быть заменена на любую другую. Таблица 10.2 - Палитры цвета

Слайд 22

Описание слайда:

Команда colorbar выводит рядом с графиком цветовую шкалу, устанавливающую соответствие между цветом и значением функции. Эту команду можно применять в сочетании со всеми функциями, строящими трехмерные объекты: Команда colorbar выводит рядом с графиком цветовую шкалу, устанавливающую соответствие между цветом и значением функции. Эту команду можно применять в сочетании со всеми функциями, строящими трехмерные объекты: colorbar Для трёхмерных графиков существует возможность изменять точку их обзора, т.е. положение виртуальной камеры с помощью функции view([az el]); где az – угол азимута; el – угол возвышения. Изменение первого угла означает вращение плоскости xOy вокруг оси Oz против часовой стрелки. Угол возвышения есть угол между направлением на камеру и плоскостью xOy.

Слайд 23

Описание слайда:

4.24 Редактирование графиков 4.24 Редактирование графиков Графики, рассмотренные выше имеют несколько недостатков: - на них не нанесена сетка из координатных линий, что затрудняет чтение графиков; - нет общей информации о кривой графика (заголовка); - неизвестно, какие величины отложены по осям графика. Рассмотрим возможности создания подписей графиков, осей и отображения сетки на графике. Для установки над графиком титульной надписи используется команда title('string'). Для установки надписей возле осей x, y и z применяются команды: xlabel('String') ylabel('String') zlabel('String') Надпись задается символьной константой или переменной 'string'.

Слайд 24

Описание слайда:

Пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него, называется легендой и создается командой legend: - legend(string1,string2,string3,…) – добавляет к текущему графику легенду в виде строк, указанных в списке параметров. - legend(string1,string2,string3,…,Pos) – помещает легенду в точно определенное место, специфицированное параметром Pos: Pos = 0 – лучшее место, выбираемое автоматически; Pos = 1 – верхний правый угол; Pos = 2 – верхний левый угол; Pos = 3 – нижний левый угол; Pos = 4 – нижний правый угол; Pos = –1 – справа от графика.

Слайд 25

Описание слайда:

Команда axis позволяет изменить масштабирование графиков: - axis([XMIN XMAX YMIN YMAX]) – установка диапазонов координат по осям x и y для текущего двумерного графика. - axis auto – установка параметров осей по умолчанию. Для улучшения чтения графиков среда MATLAB позволяет создавать масштабную сетку: - grid on – добавляет сетку к текущему графику. - grid off – отключает сетку. Для построения наложенных друг на друга графиков в одном и том же окне служит команда управления графическими построениями hold: - hold on – обеспечивает продолжение вывода графиков в текущее окно, что позволяет добавлять последующие графики к уже существующим. - hold off – отменяет режим продолжения графических построений.

Слайд 26

Описание слайда:

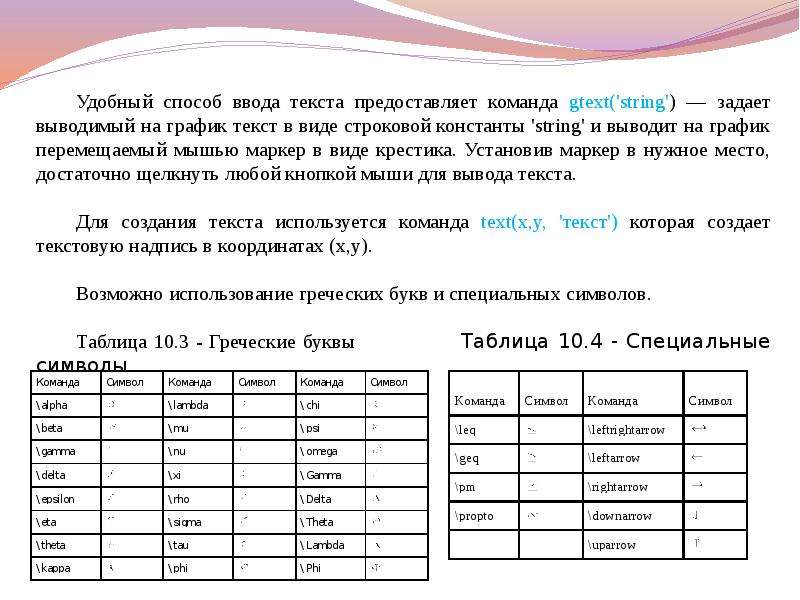
Удобный способ ввода текста предоставляет команда gtext('string') — задает выводимый на график текст в виде строковой константы 'string' и выводит на график перемещаемый мышью маркер в виде крестика. Установив маркер в нужное место, достаточно щелкнуть любой кнопкой мыши для вывода текста. Удобный способ ввода текста предоставляет команда gtext('string') — задает выводимый на график текст в виде строковой константы 'string' и выводит на график перемещаемый мышью маркер в виде крестика. Установив маркер в нужное место, достаточно щелкнуть любой кнопкой мыши для вывода текста. Для создания текста используется команда text(x,y, 'текст') которая создает текстовую надпись в координатах (х,у). Возможно использование греческих букв и специальных символов. Таблица 10.3 - Греческие буквы Таблица 10.4 - Специальные символы

Слайд 27

Описание слайда:

Для масштабирования отдельных участков трехмерных графиков, также как и в случае с двумерными графиками, используется функция Для масштабирования отдельных участков трехмерных графиков, также как и в случае с двумерными графиками, используется функция axis([xmin xmax ymin ymax zmin zmax]); Для оформления трехмерных графиков можно пользоваться описанными ранее функциями: text, xlabel, ylabel, zlabel, title, grid [on/off], subplot. Для трёхмерных графиков существует возможность изменять точку их обзора, т.е. положение виртуальной камеры с помощью функции view([az el]); где az – угол азимута; el – угол возвышения. Изменение первого угла означает вращение плоскости xOy вокруг оси Oz против часовой стрелки. Угол возвышения есть угол между направлением на камеру и плоскостью xOy. Кроме того изменить свойства линии, вывести на график обозначения осей, легенду, включить сетку можно с помощью свойств графика. Для этого необходимо нажать на пиктограмму Edit Plot и два раза щелкнуть левой кнопкой мыши на поле графика.

Слайд 28

Описание слайда:

4.25 Графики в полярных координатах 4.25 Графики в полярных координатах В полярной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат, имеющего длину R и угол ТНЕТА. Угол ТНЕТА обычно меняется от 0 до 2*pi. Для построения графиков функций в полярной системе координат используются команды типа polar(…): - polar(THETA, R) – строит график в полярной системе координат, представляющий собой положение конца радиус-вектора с длиной RHO и углом ТНЕТА; - polar(THETA,R,S) – аналогична предыдущей команде, но позволяет задавать стиль построения с помощью строковой константы S по аналогии с командой plot. Пример: phi = linspace(0, 2*pi, 200); polar(phi, sin(4*phi)); hold on; polar(phi, cos(2*phi), ’r’); hold oﬀ ;

Слайд 29

Описание слайда:

4.26 Вывод изображений 4.26 Вывод изображений Система MatLab позволяет загружать, отображать и сохранять растровые изображения, представленные в графических форматах: bmp, jpg, tiff, gif, png и т.д. Для загрузки изображений используется функция imread(FILENAME,FMT); которой в качестве параметров передается путь с указанием графического файла и формат. На выходе дается массив, соответствующий размерности изображения со значениями в формате uint8: A=imread('1024.bmp','bmp'); % A – 1024x1024 матрица uint8

Слайд 30

Описание слайда:

Если исходное изображение имеет глубину цвета не более 256, то матрица A будет двумерной и каждое ее значение будет представлять соответствующий уровень яркости точки. Если исходное изображение имеет глубину цвета не более 256, то матрица A будет двумерной и каждое ее значение будет представлять соответствующий уровень яркости точки. Если же точка исходного изображения представляется, например, 24 битами (3 байта), то матрица А будет иметь размерность 1024x1024x3, где третья размерность будет соответствовать цветовым составляющим исходного изображения. Поэтому для обработки изображений в экспериментальных целях часто используют формат с 256 градациями серого без индексации цвета. Формат uint8 не очень удобен для последующей обработки точек изображения, поэтому обычно его приводят к вещественному следующим образом: A=double(imread('1024.bmp','bmp')); В результате матрица А будет состоять из элементов типа double.

Слайд 31

Описание слайда:

Для отображения растровых изображений в графическом окне используется функция image(A); Неверное отображение изображения объясняется несоответствием палитры цветов по умолчанию (hot), заданное в MatLab, с палитрой цветов загруженного изображения (gray(256) ).

Слайд 32

Описание слайда:

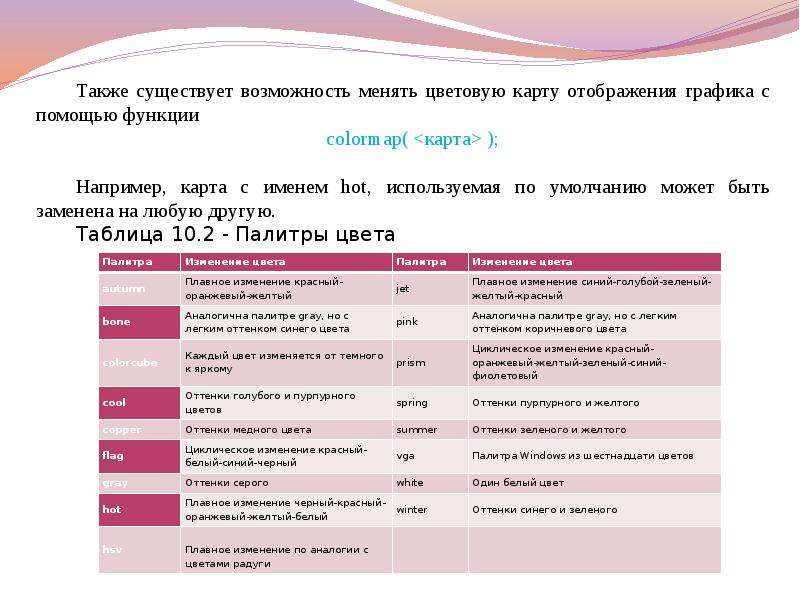
Если цветовая палитра заранее неизвестна на момент загрузки изображения, то ее можно узнать, используя второй возвращаемый параметр функции imread: Если цветовая палитра заранее неизвестна на момент загрузки изображения, то ее можно узнать, используя второй возвращаемый параметр функции imread: [A, map]=imread(‘1024.bmp’,’bmp’); image(A); colormap(map); где map – цветовая карта текущего изображения. При работе с изображениями возникают ситуации, когда диапазон значений элементов матрицы A может не соответствовать диапазону значений цветовой карты, например. В результате отображения такой матрицы на экране монитора изображение будет показываться некорректно и некоторые его детали будут незаметны. Чтобы избежать такой ситуации, диапазон значений и диапазон цветовой карты должны совпадать. Это можно выполнить автоматически с помощью функцию imagesc(A);