Сортировки. Двоичный поиск - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Сортировки. Двоичный поиск. Доклад-сообщение содержит 25 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Сортировки. Двоичный поиск.

Слайд 2

Описание слайда:

Быстрая сортировка (Ч. Хоар, 1962) Идея: «разделяй и властвуй» Среднее время работы – O(n log n) В худшем случае – O() В обычной реализации неустойчива

Слайд 3

Описание слайда:

Слайд 4

Описание слайда:

Сортировка слиянием (Дж. Фон Нейман, 1945) Идеи: «разделяй и властвуй», слияние отсортированных массивов Время работы – О() Сортировка устойчива

Слайд 5

Описание слайда:

Слайд 6

Описание слайда:

Пирамидальная сортировка Идея: использование кучи Время работы – О() Сортировка неустойчива Сортировка разбиралась на теме: «Структуры данных»

Слайд 7

Описание слайда:

Сортировка подсчётом Идея: использование конечной длины сортируемых чисел Время работы – O(n) Сортировка устойчива

Слайд 8

Описание слайда:

Слайд 9

Описание слайда:

Двоичный поиск Двоичный поиск — алгоритм поиска объекта по заданному признаку в множестве объектов, упорядоченных по тому же самому признаку, работающий за логарифмическое время.

Слайд 10

Описание слайда:

Задача Пусть нам дан упорядоченный массив, состоящий только из целочисленных элементов. Требуется найти позицию, на которой находится заданный элемент или сказать, что такого элемента нет.

Слайд 11

Описание слайда:

Принцип работы Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остаётся та часть множества, где находится искомый объект.

Слайд 12

Описание слайда:

Слайд 13

Описание слайда:

Задача Пусть у нас есть N принтеров и нам нужно напечатать К листовок. Каждый принтер печатает одну листовку за секунд. Сколько нам потребуется минимальное количество времени, чтобы напечатать все листовки? = ,

Слайд 14

Описание слайда:

Задачу можно решить с помощью двоичного поиска по ответу. Задачу можно решить с помощью двоичного поиска по ответу. Будем искать двоичным методом время, за которое мы сможем напечатать все листовки. Для каждого время мы сможем за O(N) проверить этот факт. Так как функция Количество_листовок(время) монотонна, следовательно здесь применим двоичный поиск Получим решение за O(n log ())

Слайд 15

Описание слайда:

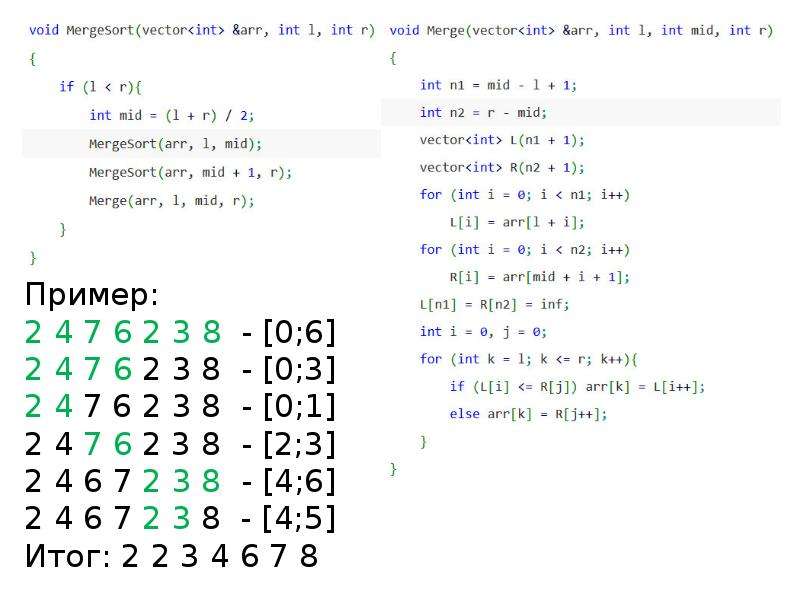
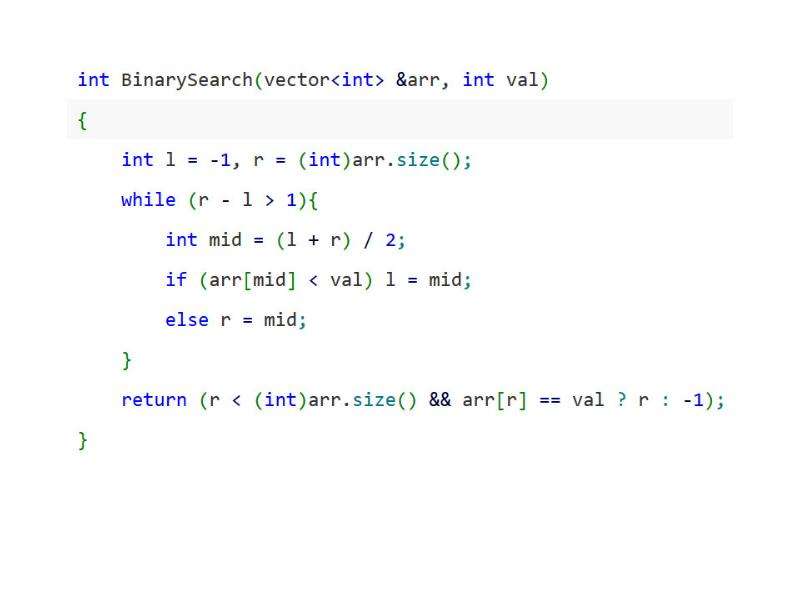
Как сам двоичный поиск, так и метод двоичного поиска по ответу очень(!) часто встречается в задачах. Как сам двоичный поиск, так и метод двоичного поиска по ответу очень(!) часто встречается в задачах. Рассмотрим ещё одну задачу: Пусть нам задана монотонная функция и два значения аргумента x1, x2. Сказано, что на отрезке [x1;x2] имеется ровно один корень функции, т.е. и f(x1)*f(x2) < 0. Нужно найти х.

Слайд 16

Описание слайда:

Некоторые полезные советы при работе с вещественными числами

Слайд 17

Описание слайда:

Когда имеешь дело с вещественными числами в первую очередь нужно подумать нельзя ли от них избавиться и перейти к целым. Когда имеешь дело с вещественными числами в первую очередь нужно подумать нельзя ли от них избавиться и перейти к целым. Пример 1: Нам нужно сравнить два числа вида a/b, где а и b целые числа

Слайд 18

Описание слайда:

Неправильный выбор: Неправильный выбор: If ((double)a/b < (double)с/d) Правильный выбор: If (a * d < c * b) Исключение: Когда a * d или c * b не помещаются в целочисленный тип

Слайд 19

Описание слайда:

Пример 2: Пример 2: Нам нужен цикл до sqrt(n) включительно. Неправильный выбор: for(int i = 0; i <= sqrt(n); i++) Правильный выбор: for(int i = 0; i * i <= n; i++)

Слайд 20

Описание слайда:

Пример 3: Пример 3: Сравнить расстояния между точками a,b и c,d int d1 = sqr(a.x-b.x) + sqr(a.y-b.y); int d2 = sqr(c.x-d.x) + sqr(c.y-d.y); Вместо: if (sqrt(d1) < sqrt(d2)) Лучше: if (d1 < d2)

Слайд 21

Описание слайда:

Если всё-таки приходится работать с вещественными числами, то всегда нужно стараться уменьшить погрешность вычислений Если всё-таки приходится работать с вещественными числами, то всегда нужно стараться уменьшить погрешность вычислений Пример 1: b/a + c/a + … = (b + c + …)/a;

Слайд 22

Описание слайда:

Пример 2: Пример 2: У нас есть прямоугольный треугольник, мы знаем длины его сторон a,b,c и один из углов A. Нужно найти sin(B) Не лучший выбор: sinb = sin(pi - A); Можно так: sinb = b/c;

Слайд 23

Описание слайда:

Если у нас возможно равенство вещественных чисел, то их всегда нужно сравнивать по eps Если у нас возможно равенство вещественных чисел, то их всегда нужно сравнивать по eps abs(a - b) < eps <=> a == b Eps должен быть меньше требуемой точности, но больше лучшей точности. Обычно выбирают eps = 1e-9; А вообще вопрос точности при работе с вещественными типами это философский вопрос 

Слайд 24

Описание слайда:

При работе с бинпоиском, если нам нужно найти число с какой-то точностью, то почти всегда лучше это делать итерационно При работе с бинпоиском, если нам нужно найти число с какой-то точностью, то почти всегда лучше это делать итерационно Пример: Нам нужно найти корень функции с заданной точностью Не правильный выбор: while((r – l) < eps) Правильный выбор: for (int i = 0; i < 100; i++)