🗊Презентация Задача о движении трёх тел

Задача о движении трёх тел

Задача трёх тел  одна из задач небесной механики, состоящая в определении относительного движения трёх тел (материальных точек), взаимодействующих по закону тяготения Ньютона (например, Солнца, Земли и Луны).

Математическая формулировка γ - гравитационная постоянная; m -массы тел; q - радиус-векторы, определяющие их положение;

Появление 1687 г., Исаак Ньютон опубликовал свои «Принципы» (Математические начала натуральной философии): первые шаги в определении и изучении проблемы движений трех массивных тел; первые шаги в применении своих результатов к лунной теории, движению Луны под действием гравитации Земли и Солнца.

Частные решения 1772г., Лагранж, мемуар «О задаче трех тел»; (изображение) 1767г., Эйлер; (изображение) 1860,1867 гг., Шарль-Эжен Делоне, для системы Солнце–Земля–Луна; 1892–1899 гг., Анри Пуанкаре, существует бесконечно много частных решений; 1911 г., Уильям Дункан Макмиллан, без основания ->1961 г. Кирилл Александрович Ситников(Проблема Ситникова); (изображение) 1970 гг., Брукса, семейство орбит Брукса-Хенона-Хаджидеметриу; 1993 г., Мур, решение, имеющее вид стабильных орбит-восьмерок; (изображение) 2013 г., Милован Шуваков, Велько Дмитрашинович, 13 частных решений;

Общий случай(Вейерштрасс) Пусть дана система произвольного числа материальных точек, взаимодействующих по закону Ньютона. Требуется, в предположении, что не произойдет соударения каких-либо двух точек, представить координаты каждой точки в виде рядов по каким-либо непрерывным функциям времени, равномерно сходящихся для всех действительных значений этой переменной.

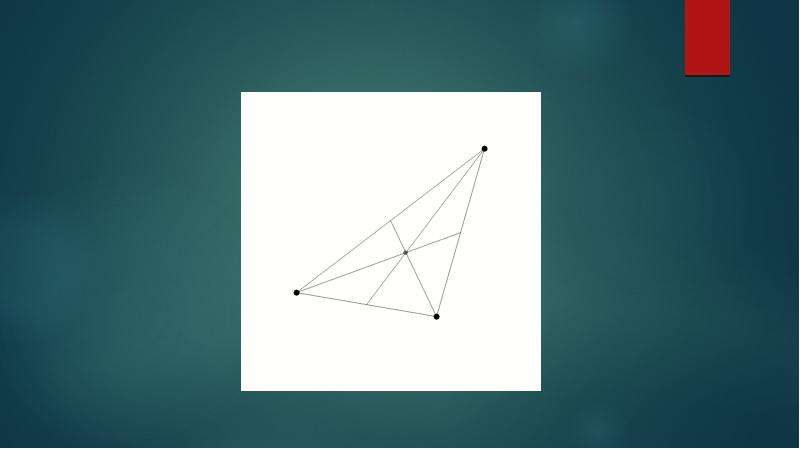
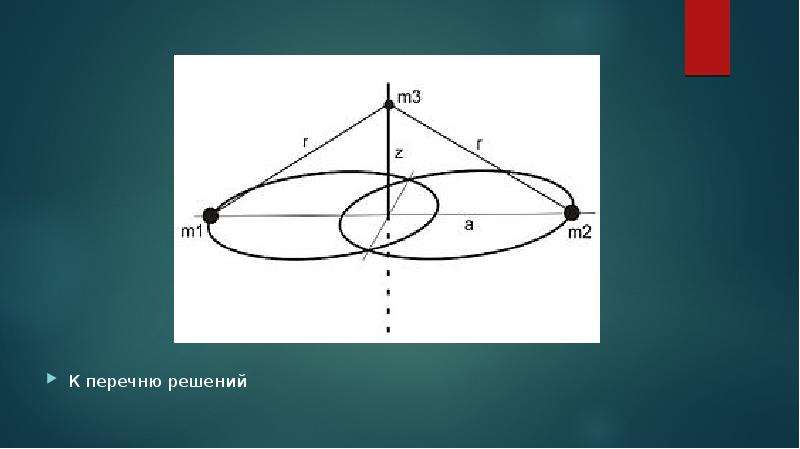
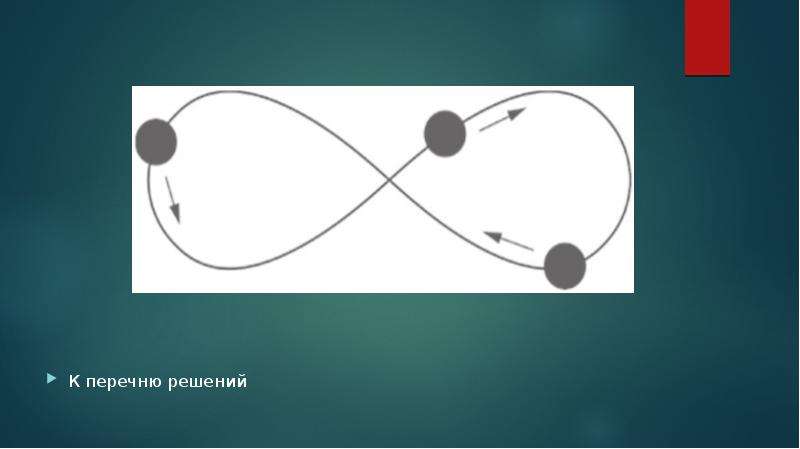
Приближённое решение Если решение задачи трёх тел является аналитической функцией t в интервале [0,t0] и перестает быть таковым при t = t0, то при t -> t0 - 0 или все расстояния между телами стремятся к нулю (тройное соударение тел), или одно из них стремится к нулю, а остальные два — к конечным пределам (простое соударение тел). (Пенлеве, 1897) Тройное соударение в задаче трёх тел возможно лишь при условии обращения в нуль момента импульса системы и, следовательно, может иметь место лишь при весьма специальных начальных данных. (Ф. А. Слудский, 1874) Если момент импульса системы не равен нулю, то существует так называемый регуляризирующий параметр s, через который можно выразить координаты и время голоморфным образом в окрестности вещественной оси s.

Ограниченная задача трех тел и точки либрации

К перечню решений К перечню решений

К перечню решений К перечню решений

К перечню решений К перечню решений