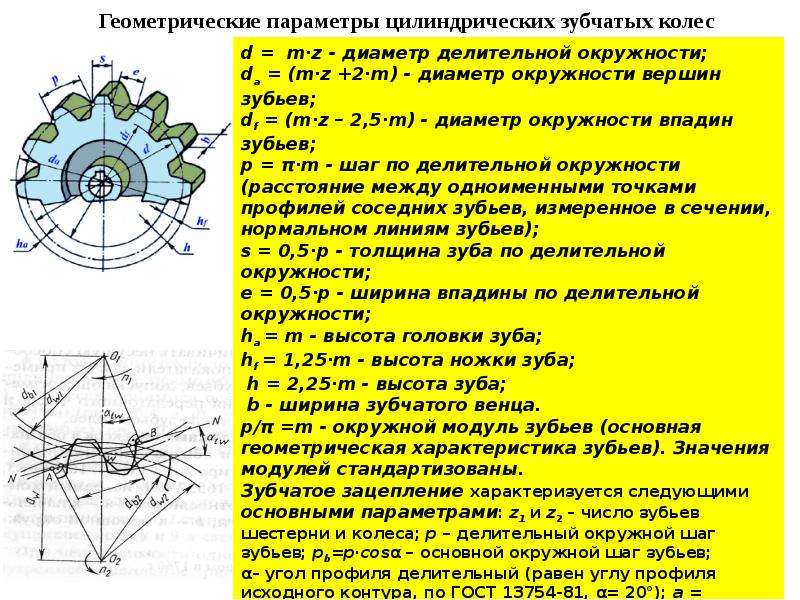
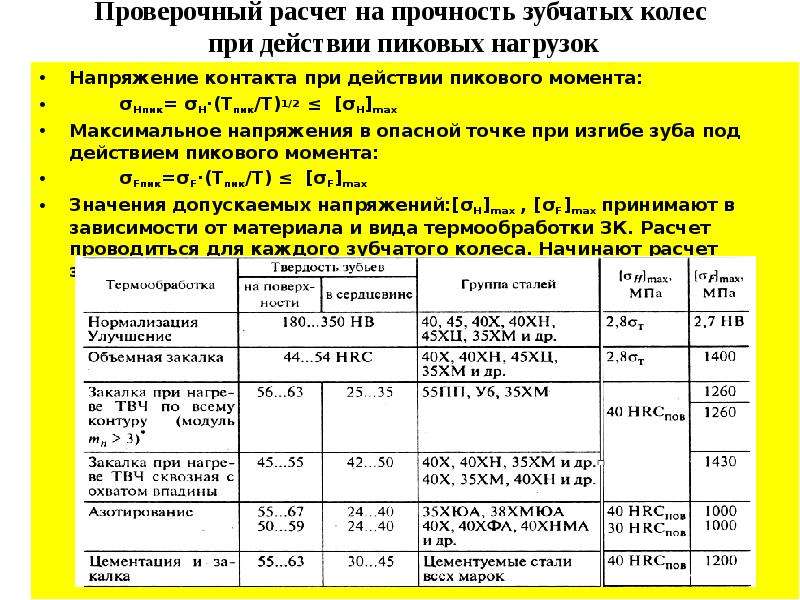
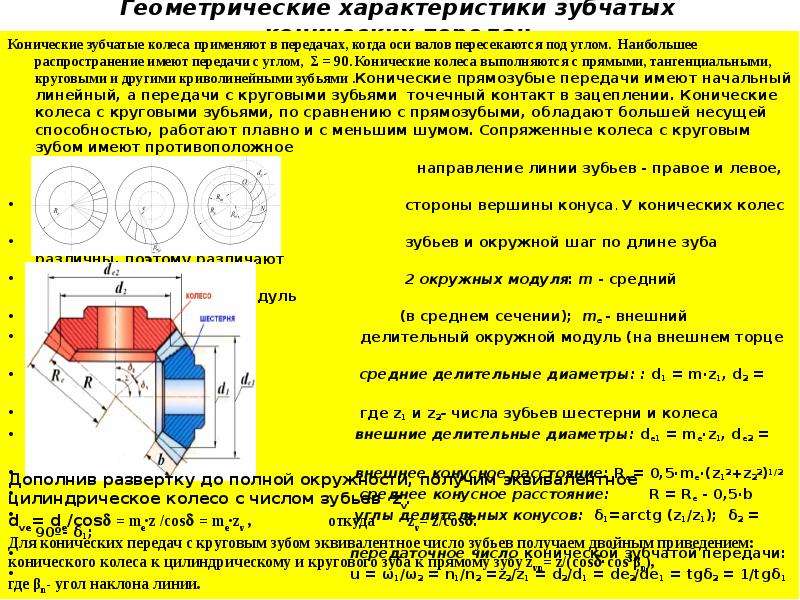
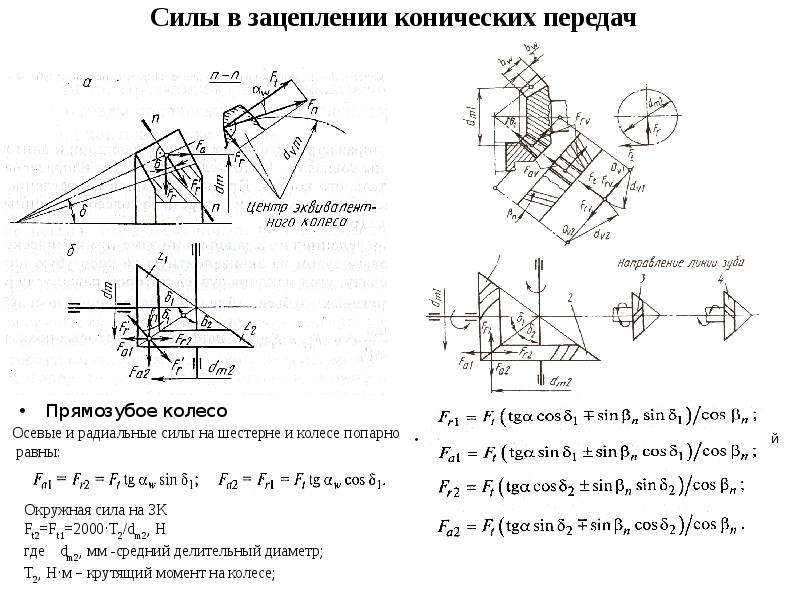
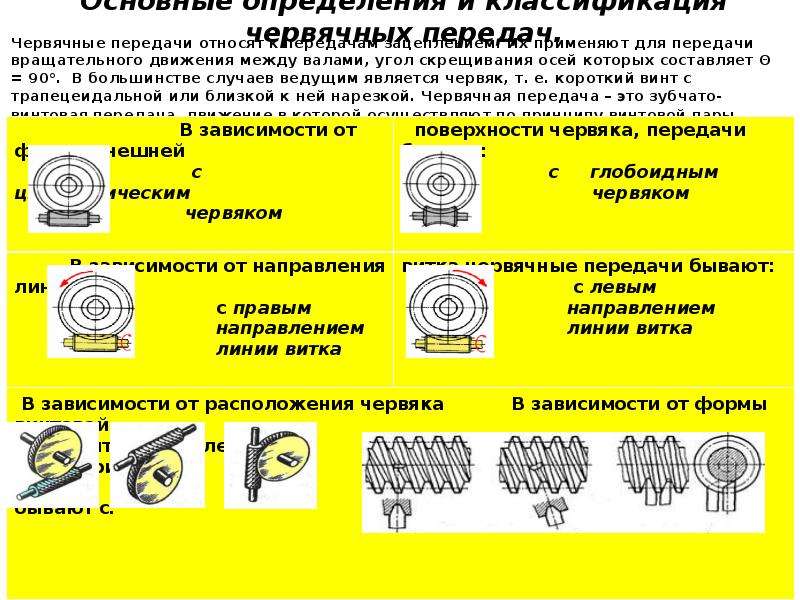
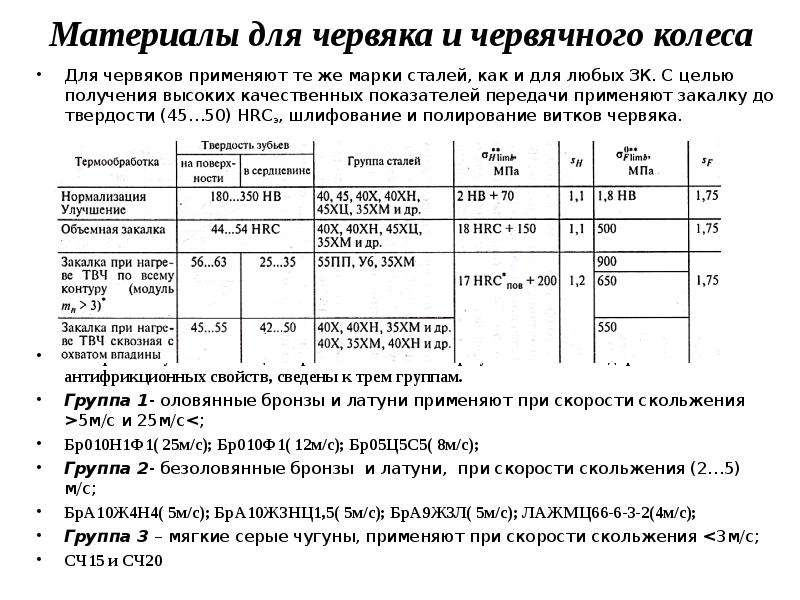
Описание слайда:
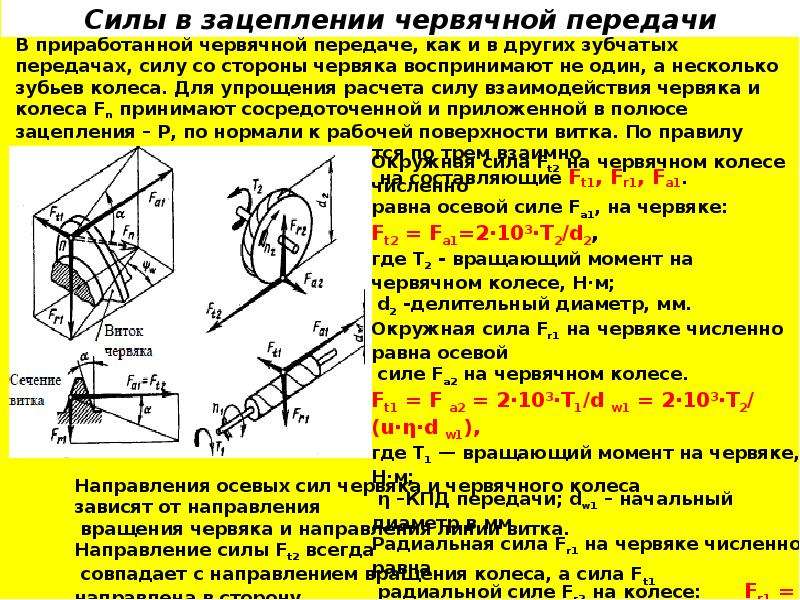
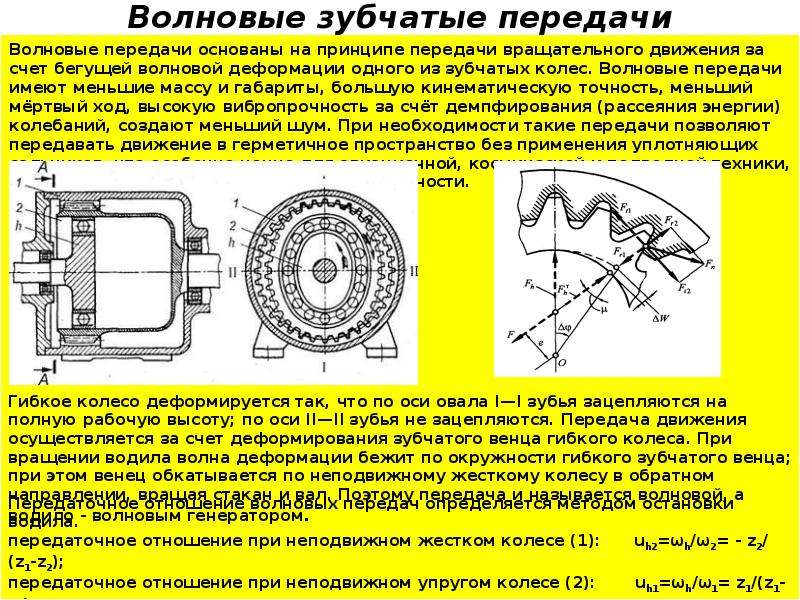
Проверочный расчет зубчатых передач по контактным напряжениям
Определяем окружную скорость :V=(π·d1·n1)/60·1000, м/с где d1, мм; n1, об/мин
Задаемся степенью точности ЗК {обычно 7, 8 , 9}
Определяем контактные напряжения σH = ZE·ZH·Zε·(( Ft2·KH·(U+1))/(d1·bw2· U))1/2 , МПа
Окружная сила на колесе: Ft2, Н∙м
Коэффициент, учитывающий механические свойства ЗК, находящихся в сопряжении
ZE=(148…192) МПа1/2
Коэффициент, учитывающий форму сопряженных поверхностей зубьев
ZH=(2·cos(βb)/tg(αwt))1/2/cos(αt), где αwt=20°, при отсутствии смещения исходного контура
αt=arctg(tg(αwt)/cosβ), βb= arcsin(sinβ/cos(αt))
Для прямозубых колес получиться : ZH=(2·cos(0)/tg(20°))1/2/cos (20°)=2,49
Коэффициент, учитывающий суммарную длину контактных линий
Zε =(1/εα)1/2, если εβ≥1, где εβ= bw2·sinβ/(π·mn)- косозубые колеса
Zε =((4-εα)/3)1/2, если εβ=0 – прямозубые колеса
Коэффициент торцевого перекрытия : εα = (1,88-3,2·(1/z1+1/z2))·cosβ , {1,5…1,7}
с увеличением β уменьшается εα , что ограничивает значение β
Коэффициент нагрузки KH = KHα· KHβ· KHv· KA
Коэффициент, учитывающий распределение нагрузки между зубьями: KHα={1,07…1,13}
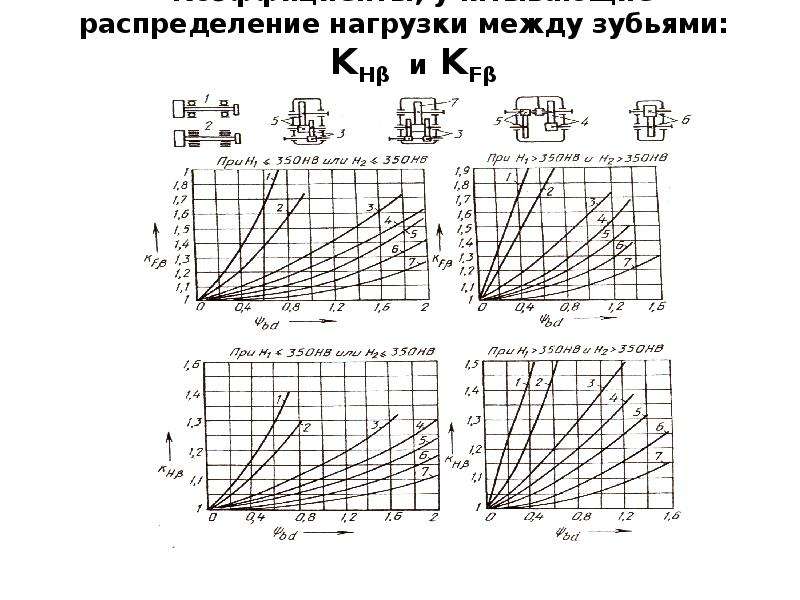
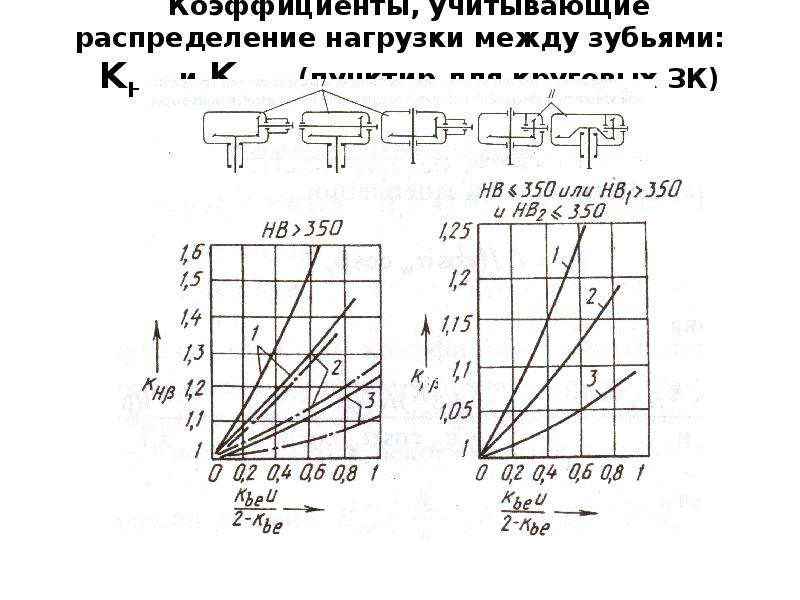
Коэффициент, учитывающий распределение нагрузки по ширине венца.
Определить по номограммам в зависимости от расположения передачи в редукторе и коэффициента ψba KHβ={1,1…1,9}
Коэффициент, учитывающий динамическую нагрузку в зацеплении: KHv=1+(wHv· bw2)/(Ft2),
где динамическая добавка wHv=δH·g0· V·( aw/ U)1/2
коэффициент, учитывающий влияние вида ЗП и модификации профиля головки ЗК
δH={0,014…0,002}, по таблицам ГОСТ 21354-87
коэффициент, учитывающий влияние шагов зацепления: g0={28…100}
Коэффициент внешней динамической нагрузки: KA=1, если изменение нагрузки учтено циклограммой. Проверяем условие: [σH] ≥ σH