🗊Презентация Diffraction grating

Diffraction grating In optics, a diffraction grating is an optical component with a periodic structure, which splits and diffracts light into several beams travelling in different directions. The emerging coloration is a form of structural coloration. The directions of these beams depend on the spacing of the grating and the wavelength of the light so that the grating acts as the dispersive element. Because of this, gratings are commonly used in monochromators and spectrometers. For practical applications, gratings generally have ridges or rulings on their surface rather than dark lines. Such gratings can be either transmissive or reflective. Gratings which modulate the phase rather than the amplitude of the incident light are also produced, frequently using holography.

The principles of diffraction gratings were discovered by James Gregory, about a year after Newton's prism experiments, initially with items such as bird feathers. The first man-made diffraction grating was made around 1785 by Philadelphia inventor David Rittenhouse, who strung hairs between two finely threaded screws. This was similar to notable German physicist Joseph von Fraunhofer's wire diffraction grating in 1821. The principles of diffraction gratings were discovered by James Gregory, about a year after Newton's prism experiments, initially with items such as bird feathers. The first man-made diffraction grating was made around 1785 by Philadelphia inventor David Rittenhouse, who strung hairs between two finely threaded screws. This was similar to notable German physicist Joseph von Fraunhofer's wire diffraction grating in 1821.

The relationship between the grating spacing and the angles of the incident and diffracted beams of light is known as the grating equation. The relationship between the grating spacing and the angles of the incident and diffracted beams of light is known as the grating equation. According to the Huygens–Fresnel principle, each point on the wavefront of a propagating wave can be considered to act as a point source, and the wavefront at any subsequent point can be found by adding together the contributions from each of these individual point sources. Gratings may be of the 'reflective' or 'transmissive' type, analogous to a mirror or lens respectively. A grating has a 'zero-order mode' (where m = 0), in which there is no diffraction and a ray of light behaves according to the laws of reflection and refraction the same as with a mirror or lens respectively.

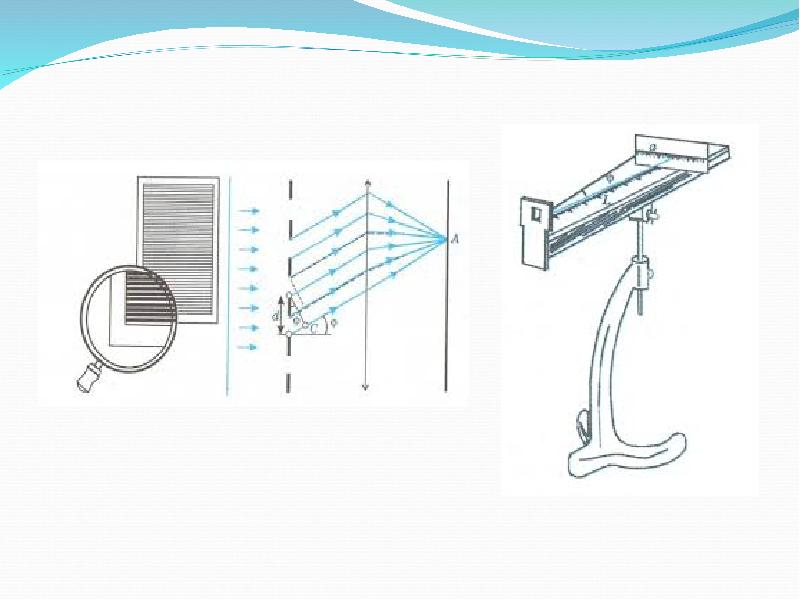
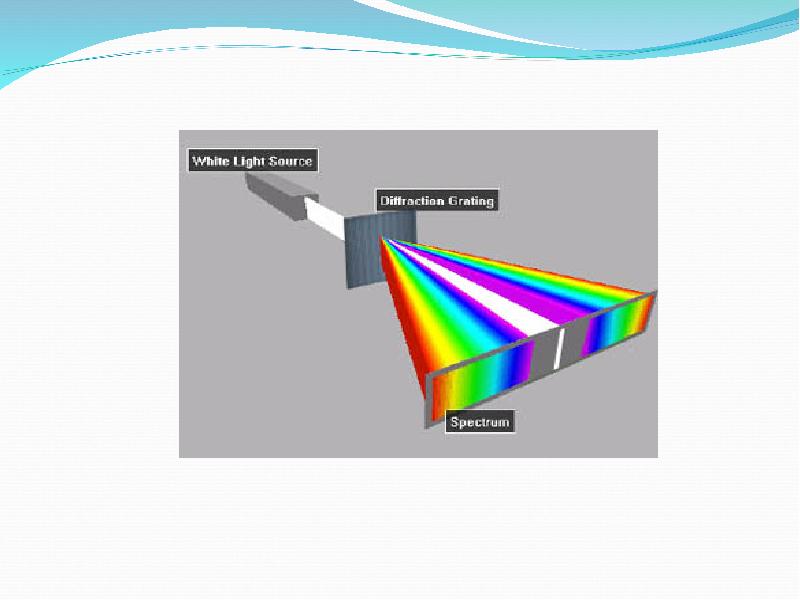
An idealised grating is considered here which is made up of a set of slits of spacing d, that must be wider than the wavelength of interest to cause diffraction. Assuming a plane wave of monochromatic light of wavelength λ with normal incidence (perpendicular to the grating), each slit in the grating acts as a quasi point-source from which light propagates in all directions (although this is typically limited to a hemisphere). After light interacts with the grating, the diffracted light is composed of the sum of interfering wave components emanating from each slit in the grating. At any given point in space through which diffracted light may pass, the path length to each slit in the grating will vary. Since the path length varies, generally, so will the phases of the waves at that point from each of the slits, and thus will add or subtract from one another to create peaks and valleys, through the phenomenon of additive and destructive interference. When the path difference between the light from adjacent slits is equal to half the wavelength, λ/2, the waves will all be out of phase, and thus will cancel each other to create points of minimum intensity. Similarly, when the path difference is λ, the phases will add together and maxima will occur. The maxima occur at angles θm, which satisfy the relationship d sinθm/λ = | m |, where θm is the angle between the diffracted ray and the grating's normal vector, and d is the distance from the center of one slit to the center of the adjacent slit, and m is an integer representing the propagation-mode of interest. An idealised grating is considered here which is made up of a set of slits of spacing d, that must be wider than the wavelength of interest to cause diffraction. Assuming a plane wave of monochromatic light of wavelength λ with normal incidence (perpendicular to the grating), each slit in the grating acts as a quasi point-source from which light propagates in all directions (although this is typically limited to a hemisphere). After light interacts with the grating, the diffracted light is composed of the sum of interfering wave components emanating from each slit in the grating. At any given point in space through which diffracted light may pass, the path length to each slit in the grating will vary. Since the path length varies, generally, so will the phases of the waves at that point from each of the slits, and thus will add or subtract from one another to create peaks and valleys, through the phenomenon of additive and destructive interference. When the path difference between the light from adjacent slits is equal to half the wavelength, λ/2, the waves will all be out of phase, and thus will cancel each other to create points of minimum intensity. Similarly, when the path difference is λ, the phases will add together and maxima will occur. The maxima occur at angles θm, which satisfy the relationship d sinθm/λ = | m |, where θm is the angle between the diffracted ray and the grating's normal vector, and d is the distance from the center of one slit to the center of the adjacent slit, and m is an integer representing the propagation-mode of interest.

The dispersion and ability to the disconnect of diffraction grating

Thanks for your attention! Thanks for your attention!