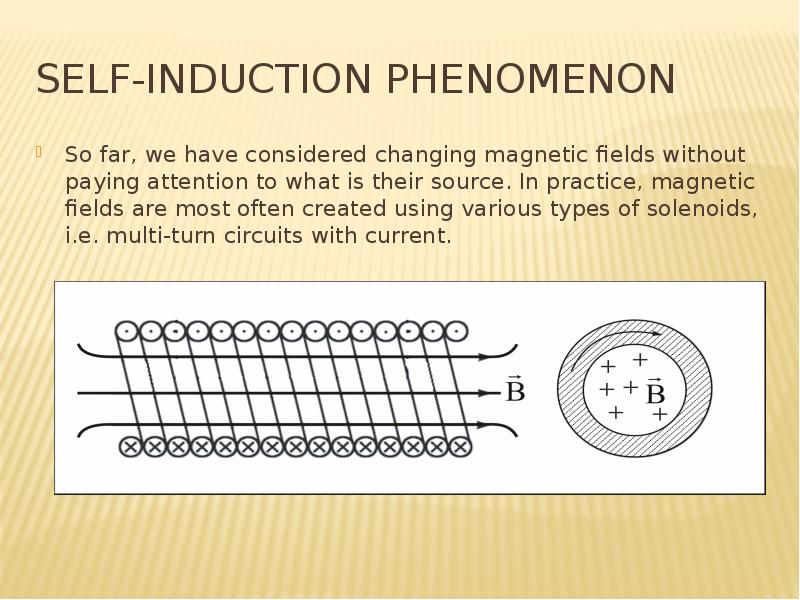
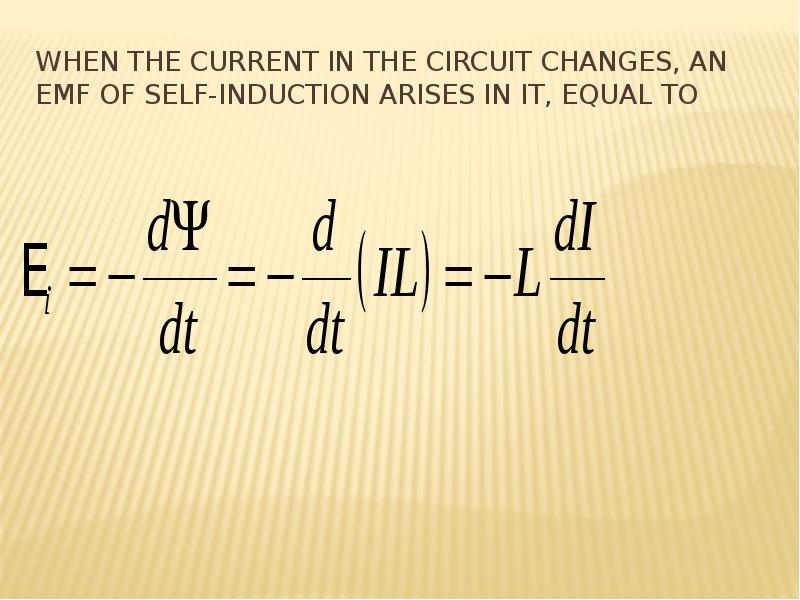
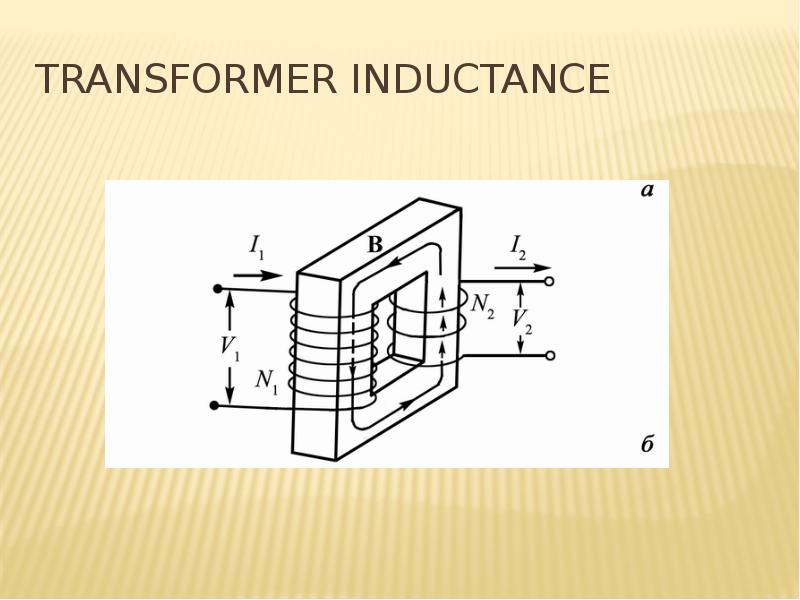
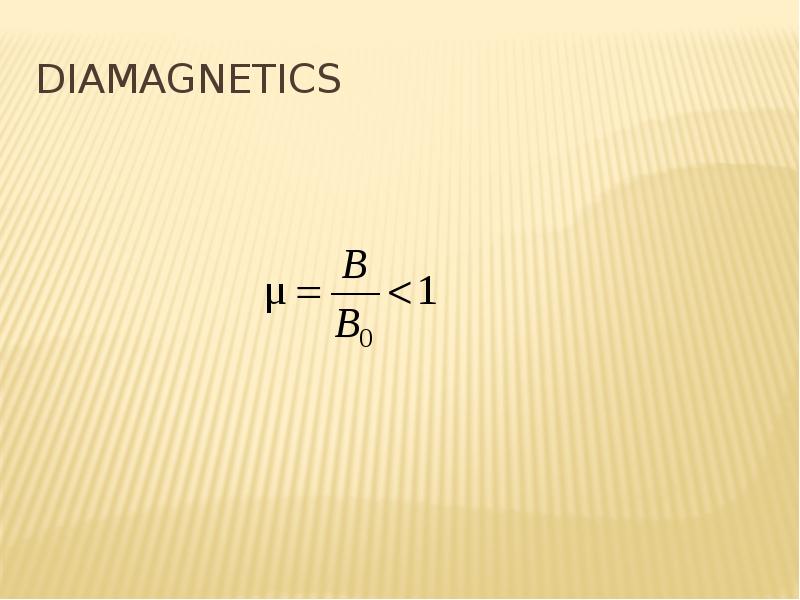
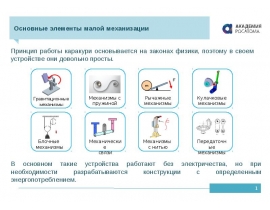
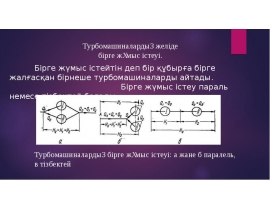
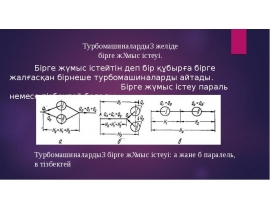
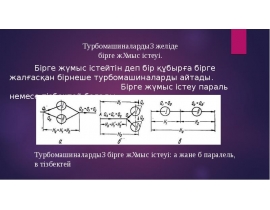
Готовые презентации на тему:
- Образование
- Искусство и Фото
- Наши презентации
- Авто/мото
- Технологии
- Бизнес и предпринимательство
- Карьера
- Данные и аналитика
- Дизайн
- Устройства и комплектующие
- Экономика и Финансы
- Машиностроение
- Развлечения и Юмор
- Путешествия
- Eда
- Политика
- Юриспруденция
- Здоровье и Медицина
- Интернет
- Инвестиции
- Закон
- Стиль жизни
- Маркетинг
- Мобильные технологии
- Новости
- Недвижимость
- Рекрутинг
- Розничная торговля
- Таможня, ВЭД, Логистика
- Наука
- Услуги
- Программное обеспечение
- Спорт
- Музыка
- Шаблоны презентации
- Детские презентации
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- История
- Литература
- Информатика
- Математика
- Обществознание
- Русский язык
- Физика
- Философия
- Химия
- МХК
- ОБЖ
- Окружающий мир
- Педагогика
- Технология
- Начальная школа
- Раскраски для детей
- Товароведение
- Менеджмент
- Страхование






































































































































































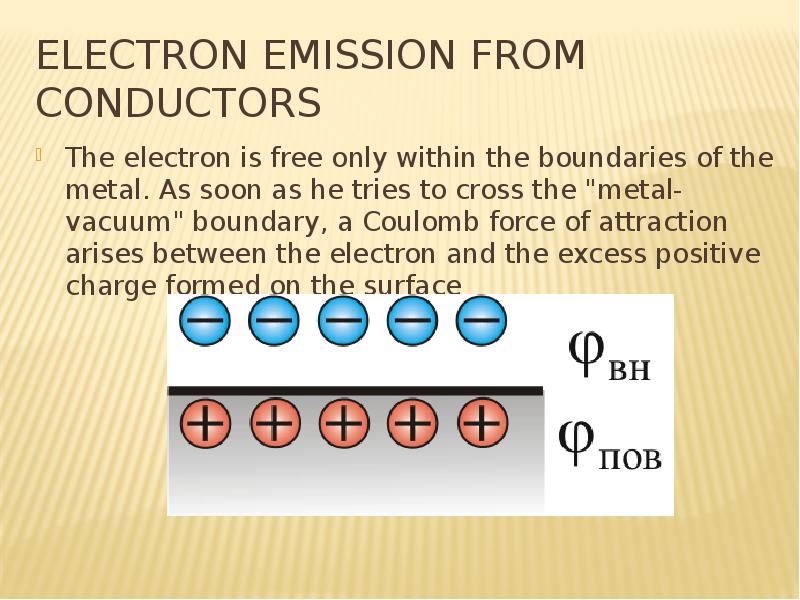



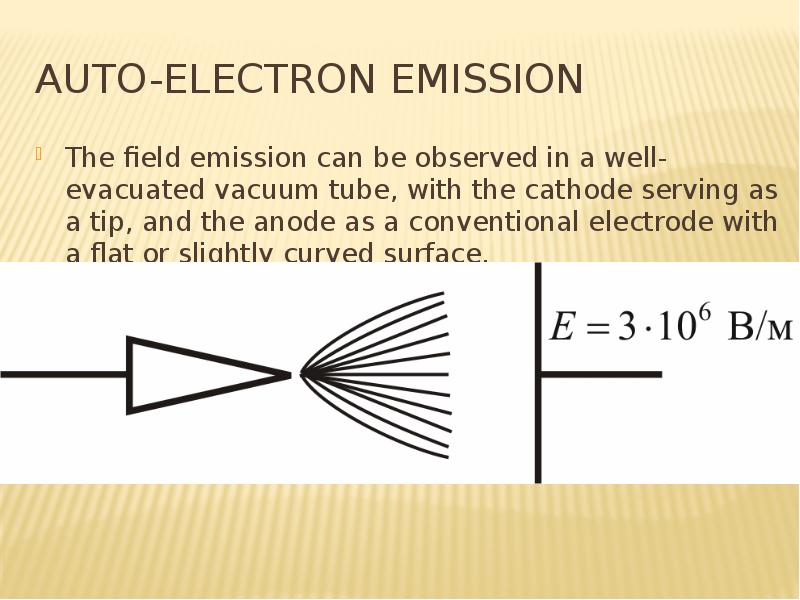
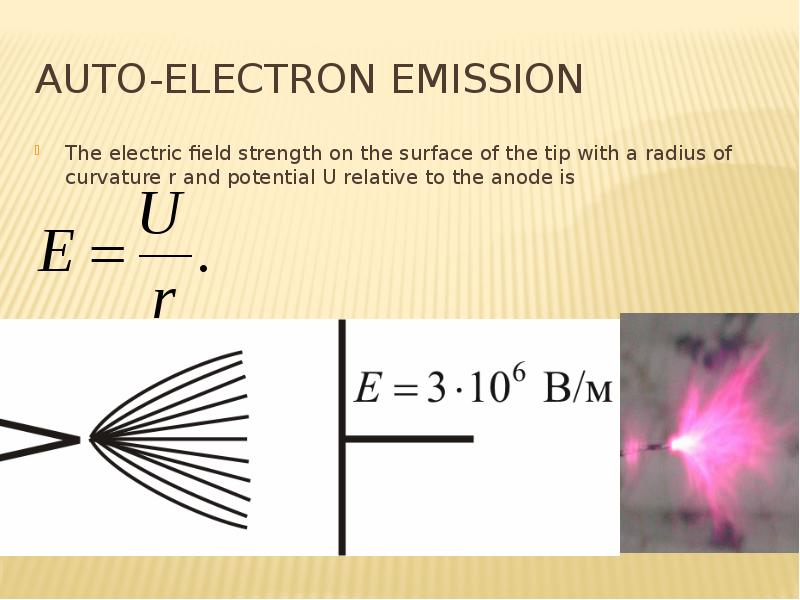


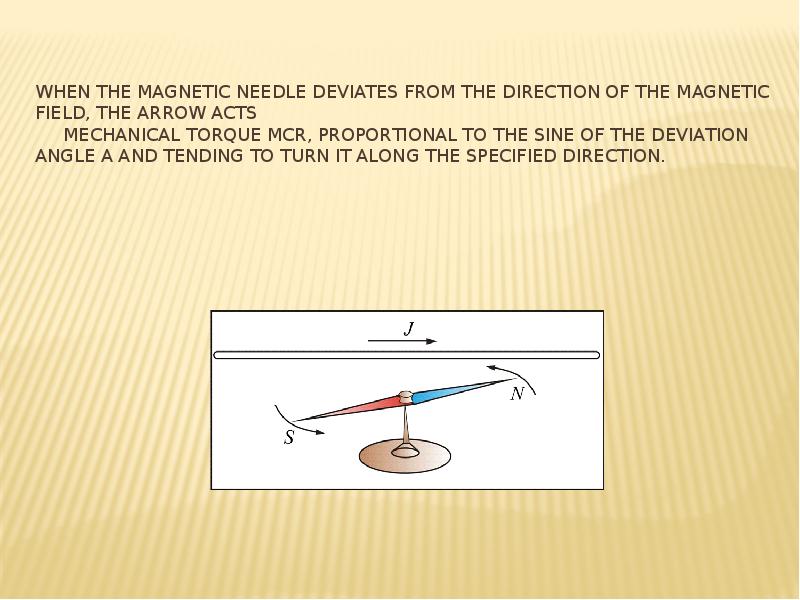

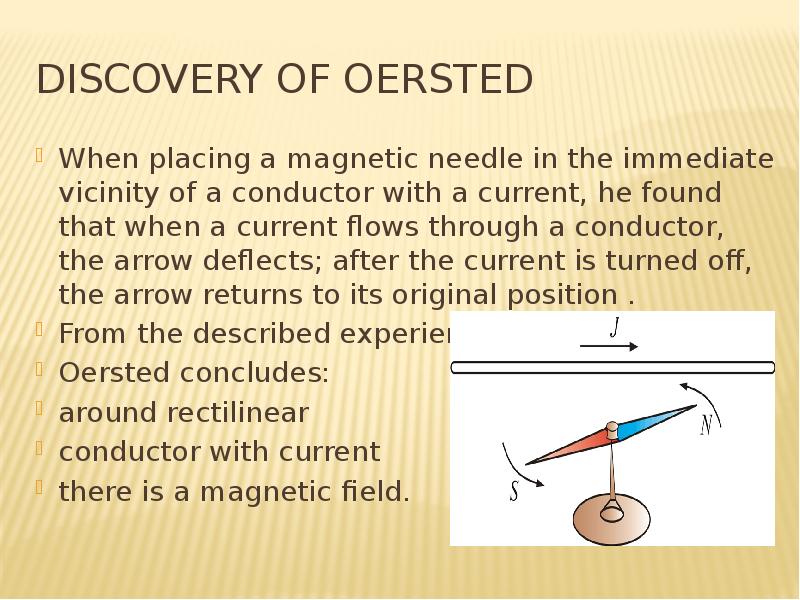


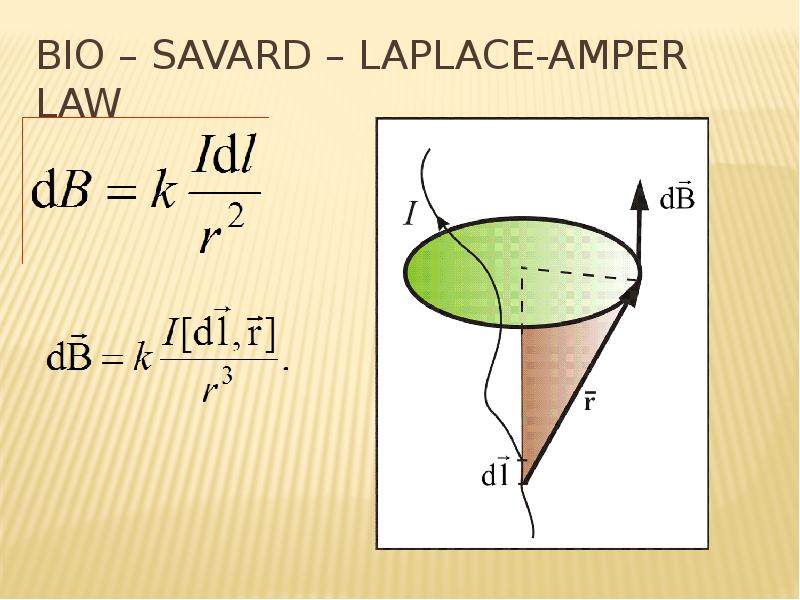





















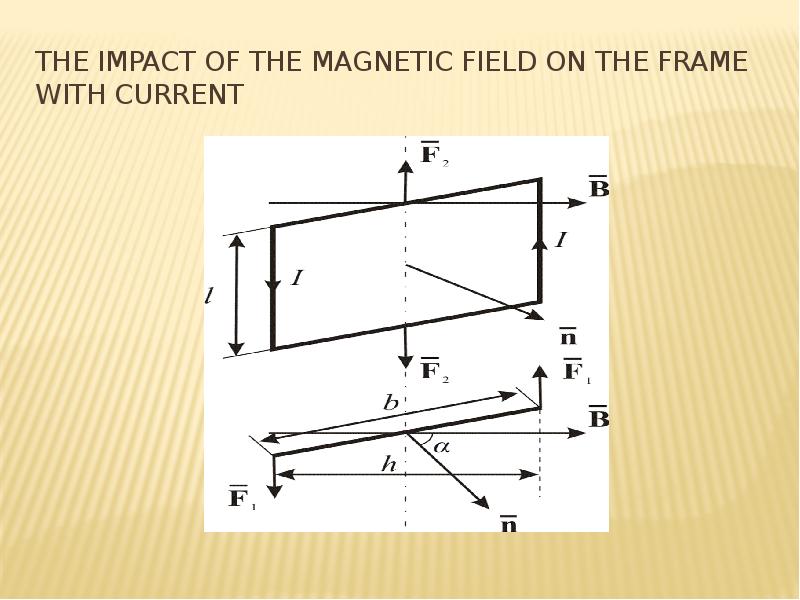


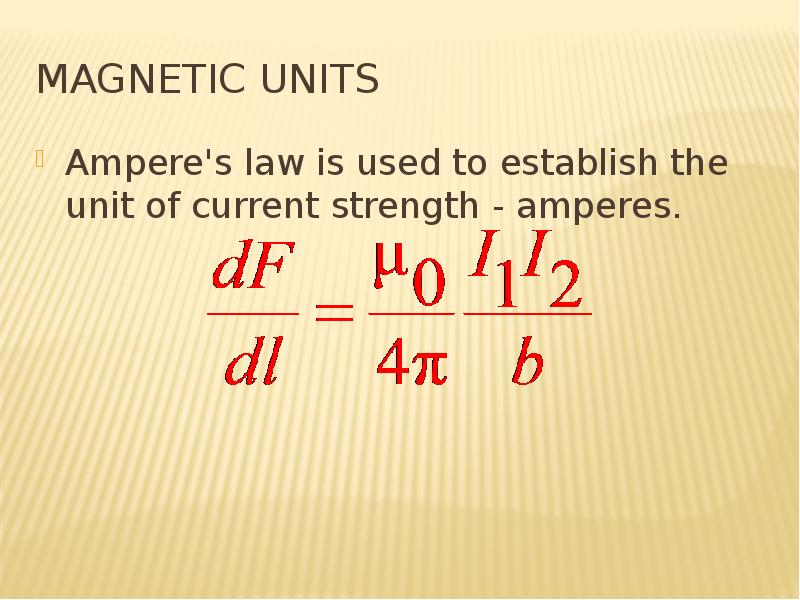



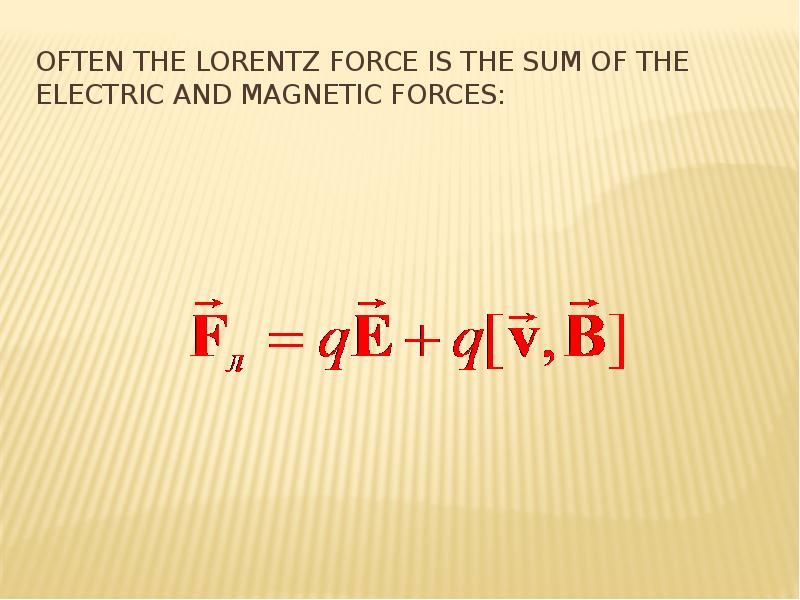
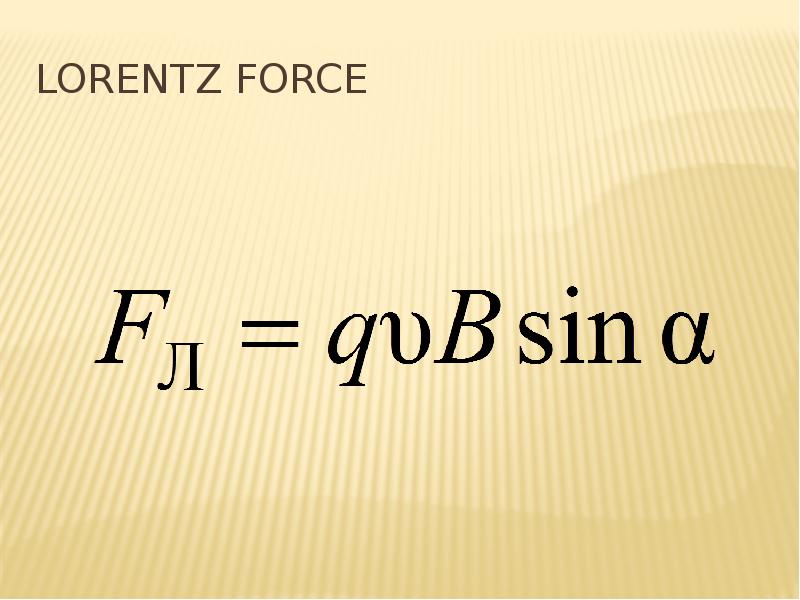
![REference
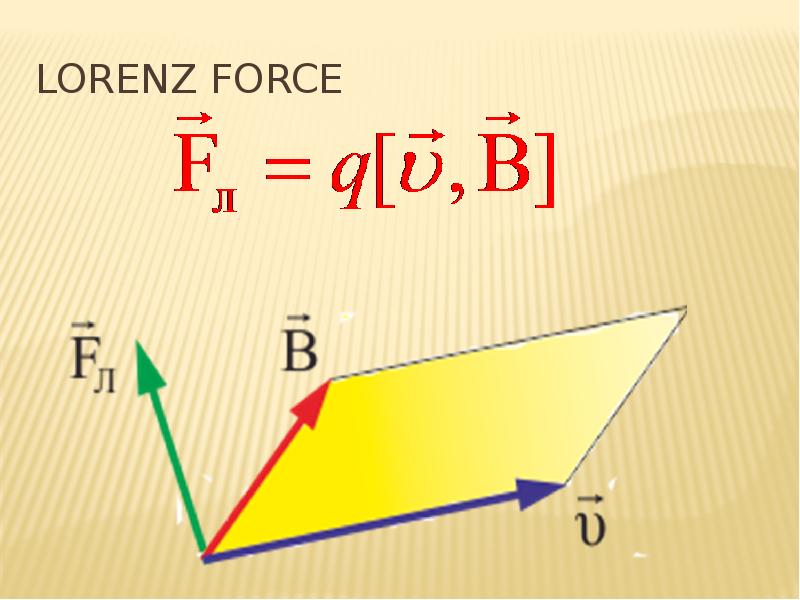
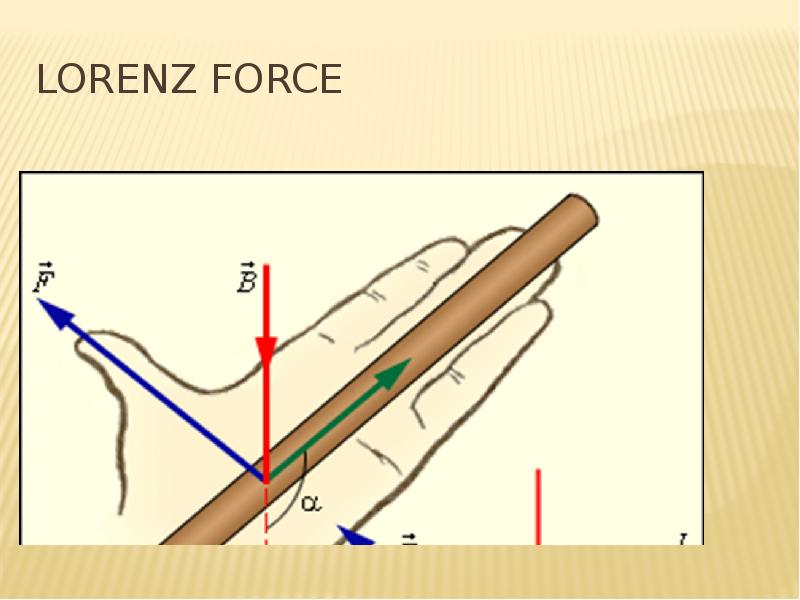
Lorenz force:
The total force acting on a charge in an electromagnetic field is
F = FE + Fm = qE + q [u, B].
The magnetic component of the Lorentz force is perpendicular to the velocity vector, the elementary work of this force is zero.
Force Fm changes the direction of motion, but not the magnitude of the speed.
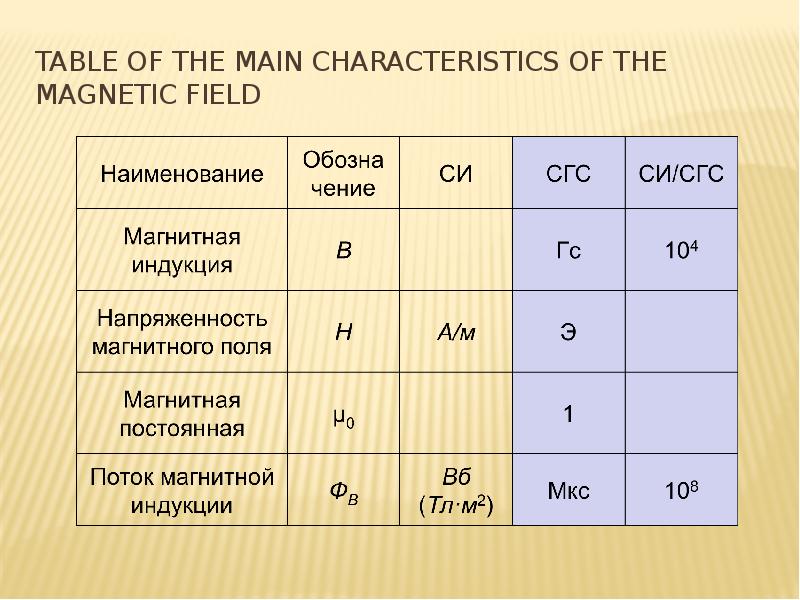
The induction of the magnetic field B is measured in SI in tesla (T).
The element dl of a conductor with current I in a magnetic field is induced by induction B, determined by the Ampere law:
dF = I [dl, B].](/documents_6/c6daf30f823f55ce9de22d4e8015b253/img244.jpg)