Кинематика колебательного движения - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Кинематика колебательного движения, слайд №1

Кинематика колебательного движения, слайд №2

Кинематика колебательного движения, слайд №3

Кинематика колебательного движения, слайд №4

Кинематика колебательного движения, слайд №5

Кинематика колебательного движения, слайд №6

Кинематика колебательного движения, слайд №7

Кинематика колебательного движения, слайд №8

Кинематика колебательного движения, слайд №9

Кинематика колебательного движения, слайд №10

Кинематика колебательного движения, слайд №11

Кинематика колебательного движения, слайд №12

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Кинематика колебательного движения. Доклад-сообщение содержит 12 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Билет №5. Кинематика колебательного движения

Слайд 2

Описание слайда:

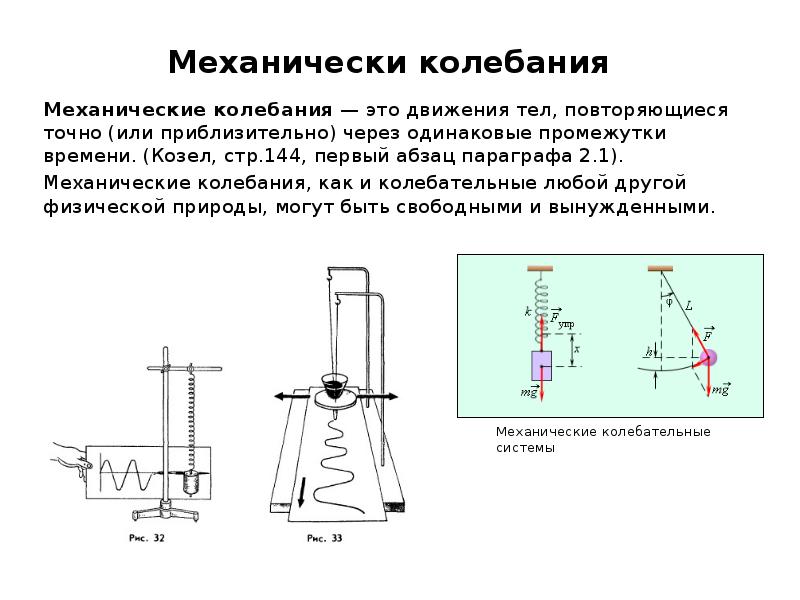
Механически колебания Механические колебания — это движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. (Козел, стр.144, первый абзац параграфа 2.1). Механические колебания, как и колебательные любой другой физической природы, могут быть свободными и вынужденными.

Слайд 3

Описание слайда:

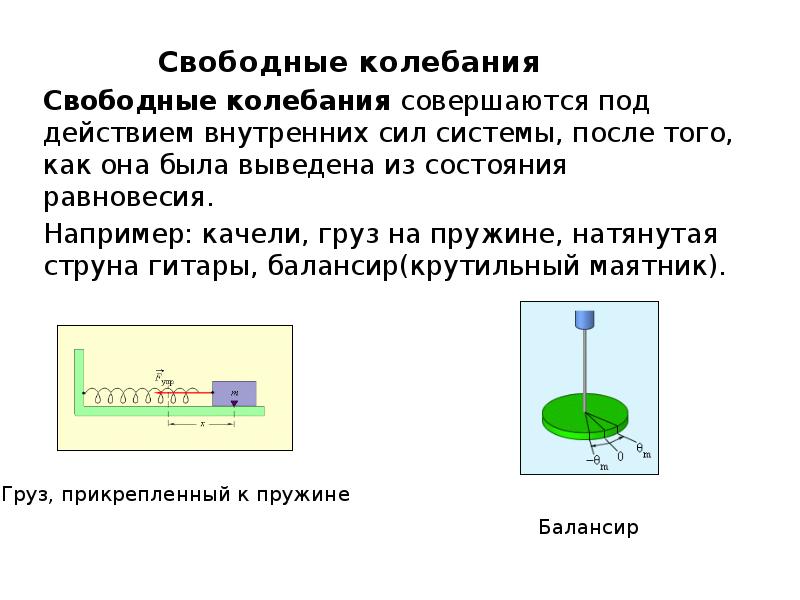
Свободные колебания Свободные колебания совершаются под действием внутренних сил системы, после того, как она была выведена из состояния равновесия. Например: качели, груз на пружине, натянутая струна гитары, балансир(крутильный маятник).

Слайд 4

Описание слайда:

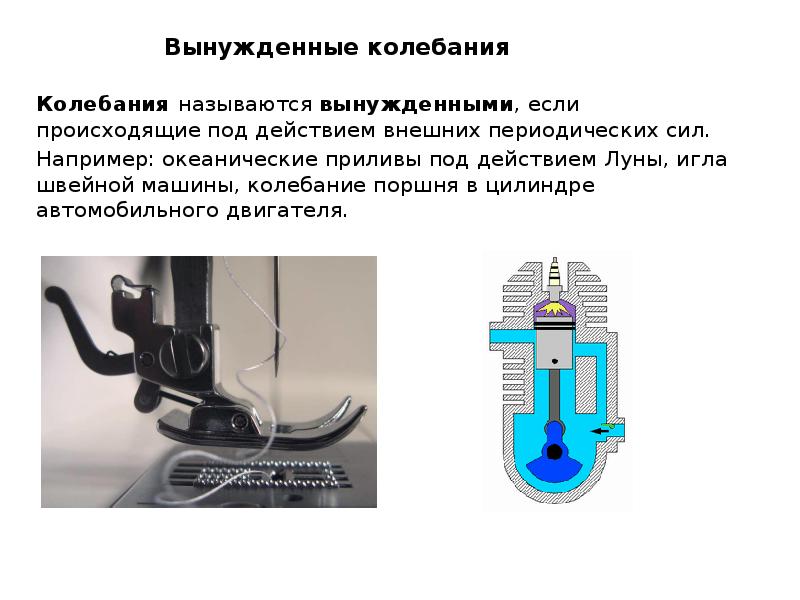
Вынужденные колебания Колебания называются вынужденными, если происходящие под действием внешних периодических сил. Например: океанические приливы под действием Луны, игла швейной машины, колебание поршня в цилиндре автомобильного двигателя.

Слайд 5

Описание слайда:

Простейшим видом колебательного процесса являются гармонические колебания. Простейшим видом колебательного процесса являются гармонические колебания. Например: колебания груза на пружине, маятник механических часов Гармонические колебания описываются законом синуса или законом косинуса. Если мы начинаем рассматривать колебание из положения максимального отклонения, то колебание опишет косинус, а если из положения равновесия, то синус.

Слайд 6

Описание слайда:

Если колебания описывать по закону косинуса, то: Если колебания описывать по закону косинуса, то: A–амплитуда колебания, [A] = 1 м; x–координата колеблющегося тела, [x] = 1 м; ϕ0– начальная фаза, [ϕ] = 1 рад; π –число «пи», константа; ω –циклическая частота, [ω] = 1 рад/с υ–скорость колеблющегося тела, [υ] = 1 м/с; a–ускорение колеблющегося тела, [a] = 1 м/с2. Важно помнить, что колебание косинуса можно описать колебанием синуса с начальной фазой ϕ0 = π/2.

Слайд 7

Описание слайда:

Если колебания описывать по закону синуса: Если колебания описывать по закону синуса: A– амплитуда колебания, [A] = 1 м; x–координата колеблющегося тела, [x] = 1 м; ϕ0– начальная фаза, [ϕ] = 1 рад; π –число «пи», константа; ω –циклическая частота, [ω] = 1 рад/с υ– скорость колеблющегося тела, [υ] = 1 м/с; a– ускорение колеблющегося тела, [a] = 1 м/с2.

Слайд 8

Описание слайда:

Из графиков видно, что своего максимального значения скорость и ускорение достигают тогда, когда множитель, содержащий тригонометрическую функцию равен 1 или –1. Из графиков видно, что своего максимального значения скорость и ускорение достигают тогда, когда множитель, содержащий тригонометрическую функцию равен 1 или –1. Отсюда несложно вывести формулы: A – амплитуда колебания, [A] = 1 м; ω –циклическая частота, [ω] = 1 рад/с ν – скорость колеблющегося тела, [υ] = 1 м/с; A – ускорение колеблющегося тела, [a] = 1 м/с2.

Слайд 9

Описание слайда:

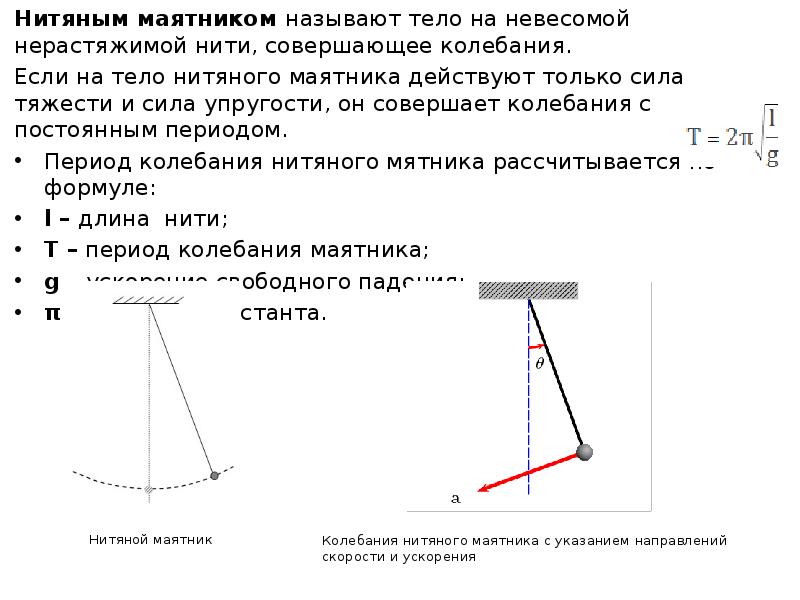
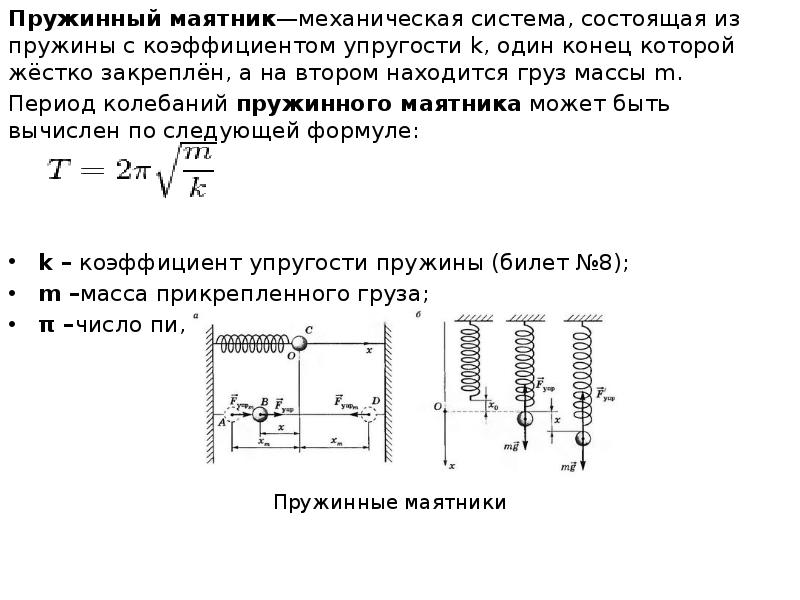
Период колебаний нитяного и пружинного маятников. Период колеба́ний маятника (T)—наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором он находился в первоначальный момент, выбранный произвольно).Измеряется в секундах [c]. Ма́ятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.

Слайд 10

Описание слайда:

Нитяным маятником называют тело на невесомой нерастяжимой нити, совершающее колебания. Нитяным маятником называют тело на невесомой нерастяжимой нити, совершающее колебания. Если на тело нитяного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. Период колебания нитяного мятника рассчитывается по формуле: l – длина нити; Т – период колебания маятника; g – ускорение свободного падения; π –число пи, константа.

Слайд 11

Описание слайда:

Маятник Фуко Ма́ятник Фуко́ — маятник, используемый для экспериментальной демонстрации суточного вращения Земли.

Слайд 12

Описание слайда:

Пружинный маятник—механическая система, состоящая из пружины с коэффициентом упругости k, один конец которой жёстко закреплён, а на втором находится груз массы m. Пружинный маятник—механическая система, состоящая из пружины с коэффициентом упругости k, один конец которой жёстко закреплён, а на втором находится груз массы m. Период колебаний пружинного маятника может быть вычислен по следующей формуле: k – коэффициент упругости пружины (билет №8); m –масса прикрепленного груза; π –число пи, константа.