Комбинаторика. Правила и формулы - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Комбинаторика. Правила и формулы, слайд №1

Комбинаторика. Правила и формулы, слайд №2

Комбинаторика. Правила и формулы, слайд №3

Комбинаторика. Правила и формулы, слайд №4

Комбинаторика. Правила и формулы, слайд №5

Комбинаторика. Правила и формулы, слайд №6

Комбинаторика. Правила и формулы, слайд №7

Комбинаторика. Правила и формулы, слайд №8

Комбинаторика. Правила и формулы, слайд №9

Комбинаторика. Правила и формулы, слайд №10

Комбинаторика. Правила и формулы, слайд №11

Комбинаторика. Правила и формулы, слайд №12

Комбинаторика. Правила и формулы, слайд №13

Комбинаторика. Правила и формулы, слайд №14

Комбинаторика. Правила и формулы, слайд №15

Комбинаторика. Правила и формулы, слайд №16

Комбинаторика. Правила и формулы, слайд №17

Комбинаторика. Правила и формулы, слайд №18

Комбинаторика. Правила и формулы, слайд №19

Комбинаторика. Правила и формулы, слайд №20

Комбинаторика. Правила и формулы, слайд №21

Комбинаторика. Правила и формулы, слайд №22

Комбинаторика. Правила и формулы, слайд №23

Комбинаторика. Правила и формулы, слайд №24

Комбинаторика. Правила и формулы, слайд №25

Комбинаторика. Правила и формулы, слайд №26

Комбинаторика. Правила и формулы, слайд №27

Комбинаторика. Правила и формулы, слайд №28

Комбинаторика. Правила и формулы, слайд №29

Комбинаторика. Правила и формулы, слайд №30

Комбинаторика. Правила и формулы, слайд №31

Комбинаторика. Правила и формулы, слайд №32

Комбинаторика. Правила и формулы, слайд №33

Комбинаторика. Правила и формулы, слайд №34

Комбинаторика. Правила и формулы, слайд №35

Комбинаторика. Правила и формулы, слайд №36

Комбинаторика. Правила и формулы, слайд №37

Комбинаторика. Правила и формулы, слайд №38

Комбинаторика. Правила и формулы, слайд №39

Комбинаторика. Правила и формулы, слайд №40

Комбинаторика. Правила и формулы, слайд №41

Комбинаторика. Правила и формулы, слайд №42

Комбинаторика. Правила и формулы, слайд №43

Комбинаторика. Правила и формулы, слайд №44

Комбинаторика. Правила и формулы, слайд №45

Комбинаторика. Правила и формулы, слайд №46

Комбинаторика. Правила и формулы, слайд №47

Комбинаторика. Правила и формулы, слайд №48

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Комбинаторика. Правила и формулы. Доклад-сообщение содержит 48 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Комбинаторика Правила и формулы

Слайд 2

Описание слайда:

Правило суммы Если элемент x можно выбрать способами nx и если элемент y можно выбрать ny способами, то выбор «либо x, либо y» можно осуществить способами nx+ ny.

Слайд 3

Описание слайда:

Правило суммы Правило суммы используется тогда, когда варианты соединяются словом «ИЛИ»

Слайд 4

Описание слайда:

Пример 1 Сколько различных символов можно закодировать, используя код Морзе длиной не менее 5 и (или) не более 6 сигналов(точек и тире)? Одновременно это никак не может произойти.

Слайд 5

Описание слайда:

Правило произведения Если элемент x можно выбрать nx способами и если после его выбора элемент y можно выбрать ny способами, то выбор упорядоченной пары (x, y) можно осуществить nx∙ ny способами.

Слайд 6

Описание слайда:

Пример 2. Номер автомобиля состоит из шести мест, на первом – буква, затем – три цифры, за ними еще две буквы. Сколько существует автомобильных номеров ? Пример 2. Номер автомобиля состоит из шести мест, на первом – буква, затем – три цифры, за ними еще две буквы. Сколько существует автомобильных номеров ? Могут быть использованы любые из 33 букв русского алфавита, кроме «ь», «ъ» и «й». Решение. На первое место можно поставить любую из 30 букв. На второе, третье, четвертое – любую из 10-ти цифр. На пятое, шестое место можно поставить любую из 30-ти букв. По правилу умножения имеем: 30*10*10*10*30*30=27*106 Такое количество номеров автомобилей может быть выдано ГАИ в Саратовской области

Слайд 7

Описание слайда:

Формулы комбинаторики Перестановки Размещения Сочетания

Слайд 8

Описание слайда:

Два главных вопроса В задаче требуется переставить все элементы или требуется выбрать несколько из них? (все элементы – перестановки, выбрать несколько – сочетания или размещения). Если нужен выбор, то важен ли порядок? Если важен – размещения, если не важен – сочетания.

Слайд 9

Описание слайда:

Перестановки Используются все элементы Порядок элементов важен

Слайд 10

Описание слайда:

Перестановки без повторений Перестановками без повторений из n различных элементов называются все возможные последовательности этих n элементов. Число перестановок без повторений из n элементов равняется по определению

Слайд 11

Описание слайда:

Перестановки без повторений

Слайд 12

Описание слайда:

Пример 4.Сколькими способами можно расставить на полке 4 книги ? (Обозначим их А, В, С,D ). Основным различием этих размещений служит порядок объектов; изменение порядка дает другое размещение. 4*3*2*1=24

Слайд 13

Описание слайда:

Пример 5 По следствию должны пройти пять человек: A, B, C, D, E. Cколько вариантов того, что в списке из этих пяти человек, составленном случайным образом B будет следовать сразу после A?

Слайд 14

Описание слайда:

Решение АВ??? - таких вариантов Р3=3!=6 ?АВ?? ??АВ? ???АВ Всего вариантов М=6*4=24

Слайд 15

Описание слайда:

Перестановки с повторениями Перестановки с повторением из n элементов k типов число элементов 1-го типа n1; число элементов 2-го типа n2; число элементов k-го типа nk, все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают подсчитывают так:

Слайд 16

Описание слайда:

Перестановки с повторениями

Слайд 17

Описание слайда:

Пример 6. Сколько чисел можно создать из двух цифр «2» и двух цифр «1»? Пример 6. Сколько чисел можно создать из двух цифр «2» и двух цифр «1»? 1122 1212 1221 2211 2121 2112 4!/2!/2!=6

Слайд 18

Описание слайда:

Пример 7. Существует конечное число неэквивалентных друг другу логических функций, зависящих от трех аргументов. Среди них есть функции, для каждой из которых существует только два набора значений аргументов, при которых функция становится тождественно равна значению "Истина" (для всех остальных наборов значений аргументов такая функция тождественно равна значению "Ложь"). Сколько существует таких функций? В ответе укажите целое число.

Слайд 19

Описание слайда:

Решение 8!/(2!*6!)=23

Слайд 20

Описание слайда:

Размещения (выборки) Используются не все элементы Порядок элементов важен

Слайд 21

Описание слайда:

Размещения без повторений Размещениями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n, которые отличаются друг от друга или порядком следования элементов, или составом элементов. Число размещений без повторений из n элементов по m обозначается символом

Слайд 22

Описание слайда:

Размещения без повторений

Слайд 23

Описание слайда:

Пример 8 В фирме работают 8 человек одинаковой квалификации, среди них Иванов, Петров, Сидоров. Сколькими способами можно случайно выбрать трех из восьми?

Слайд 24

Описание слайда:

Решение Всего вариантов - выбрать три из восьми без повторения, т.к. один и тот же не может выполнять две работы

Слайд 25

Описание слайда:

Размещения с повторениями Размещения с повторениями из элементов k типов по m элементов (k и m могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличаются друг от друга или порядком следования элементов, или составом элементов.

Слайд 26

Описание слайда:

Размещения с повторениями

Слайд 27

Описание слайда:

Пример 9 Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; на секторах каждого из дисков написаны цифры 0, 1, …, 9. Какова вероятность открыть закрытую камеру для человека: забывшего все, что он набрал на дисках, закрывая камеру; помнящего только цифру, набранную на первом диске; помнящего только, что ни на втором, ни на третьем, ни на четвертом, диске не набирал цифру 6?

Слайд 28

Описание слайда:

Решение 1) Всего вариантов 2) Всего вариантов 3) Всего вариантов N=10*9*9*9

Слайд 29

Описание слайда:

Сочетания Используются не все элементы Порядок элементов не важен

Слайд 30

Описание слайда:

Сочетания без повторений Сочетаниями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n, которые отличаются друг от друга составом элементов.

Слайд 31

Описание слайда:

Сочетания без повторений

Слайд 32

Описание слайда:

Пример 10 В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии. Сколько всего партий было сыграно?

Слайд 33

Описание слайда:

Решение

Слайд 34

Описание слайда:

Сочетания с повторениями Сочетаниями с повторениями из элементов k типов по m элементов (m и k могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличают друг от друга составом элементов.

Слайд 35

Описание слайда:

Сочетания с повторениями

Слайд 36

Описание слайда:

Пример 11 Имеется 2 типа цветов, количество цветов не ограничено. Сколько различных букетов можно составить из 3-х цветов? 111 222 122 211 Всего 4 различных букета

Слайд 37

Описание слайда:

Пример 12 Имеется 5 типов цветов, количество цветов не ограничено. Сколько различных букетов можно составить из 3-х цветов?

Слайд 38

Описание слайда:

Решение Сочетание с повторением: (5+3-1)!/(3!*(5-1) !)=35

Слайд 39

Описание слайда:

Слайд 40

Описание слайда:

Пример 13. Сколькими способами можно выбрать четырех студентов, которые будут получать стипендию, из восьми. Решение. Мы выбираем четырех из восьми, следовательно, это не "перестановки", а "сочетания" или "размещения". Так как студенты все разные, и один студент не может получать две или более стипендий, то должна использоваться формула "без повторений". Так как по условию задачи не сказано, что стипендии разные по величине, то порядок отбора нам не важен. Следовательно, нам нужна формула "сочетания без повторений". Всего студентов: n=8 , количество выбираемых: m=4 . 8!/4!/(8-4)!=70 вариантов. Пример 13. Сколькими способами можно выбрать четырех студентов, которые будут получать стипендию, из восьми. Решение. Мы выбираем четырех из восьми, следовательно, это не "перестановки", а "сочетания" или "размещения". Так как студенты все разные, и один студент не может получать две или более стипендий, то должна использоваться формула "без повторений". Так как по условию задачи не сказано, что стипендии разные по величине, то порядок отбора нам не важен. Следовательно, нам нужна формула "сочетания без повторений". Всего студентов: n=8 , количество выбираемых: m=4 . 8!/4!/(8-4)!=70 вариантов.

Слайд 41

Описание слайда:

Пример 14. Паша, Сережа, Андрей и Антон думают надеть ли на торжественный вечер галстуки или бабочки. Они хотят одеться так, чтобы количество бабочек было нечетным. Перечислите все способы так одеться. Решение. Хотя нас и не спрашивают, сколько вариантов, давайте найдем их количество, чтобы потом проверить себя. Если бабочек должно быть нечетное число, то бабочка может быть или одна, или три. Найдем, сколько вариантов может быть, если бабочка одна. 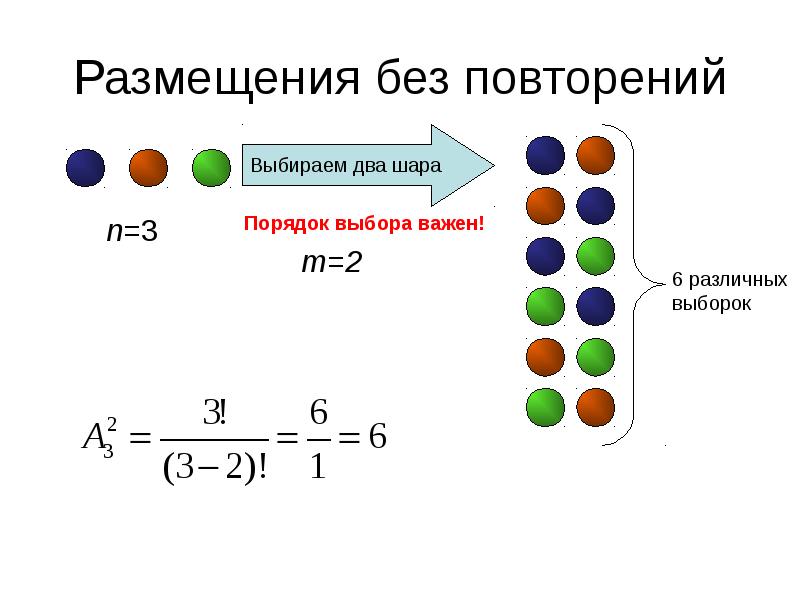Воспользуемся формулой сочетания без повторений. Всего ребят четверо n=4, выбираем одного, кто оденет бабочку m=1 . 4!/1!/(4-1)!=4 Теперь найдем количество вариантов, когда бабочек будет три. 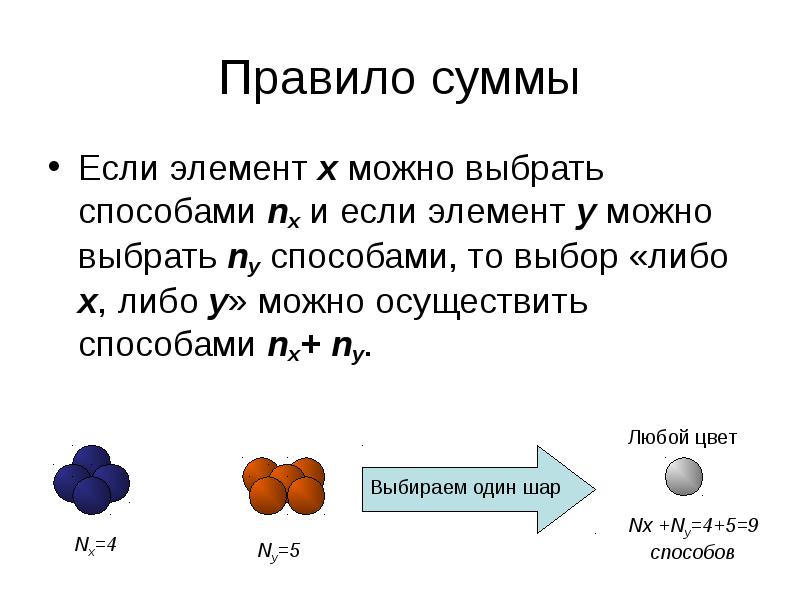4!/3!/(4-3)!=4, Найдем общее количество вариантов одеваний, воспользовавшись правилом суммы 4+4=8. Теперь собственно сделаем то, что требовалось в задаче. Паша Сережа Андрей Антон 1Галстук Галстук Галстук Бабочка 2Галстук Галстук Бабочка Галстук Пример 14. Паша, Сережа, Андрей и Антон думают надеть ли на торжественный вечер галстуки или бабочки. Они хотят одеться так, чтобы количество бабочек было нечетным. Перечислите все способы так одеться. Решение. Хотя нас и не спрашивают, сколько вариантов, давайте найдем их количество, чтобы потом проверить себя. Если бабочек должно быть нечетное число, то бабочка может быть или одна, или три. Найдем, сколько вариантов может быть, если бабочка одна. Воспользуемся формулой сочетания без повторений. Всего ребят четверо n=4, выбираем одного, кто оденет бабочку m=1 . 4!/1!/(4-1)!=4 Теперь найдем количество вариантов, когда бабочек будет три. 4!/3!/(4-3)!=4, Найдем общее количество вариантов одеваний, воспользовавшись правилом суммы 4+4=8. Теперь собственно сделаем то, что требовалось в задаче. Паша Сережа Андрей Антон 1Галстук Галстук Галстук Бабочка 2Галстук Галстук Бабочка Галстук 3Галстук Бабочка Галстук Галстук 4Бабочка Галстук Галстук Галстук 5Галстук Бабочка Бабочка Бабочка 6Бабочка Бабочка Бабочка Галстук 7Бабочка Бабочка Галстук Бабочка 8Бабочка Галстук Бабочка Бабочка

Слайд 42

Описание слайда:

Задача1 Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?

Слайд 43

Описание слайда:

Задача 2 Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи четырех сигнальных флагов, если на корабле имеются флаги трех различных видов (флагов каждого вида неограниченное количество)?

Слайд 44

Описание слайда:

Задача 3 Вася и Петя передают друг другу сообщения, используя синий, красный и зеленый фонарики. Это они делают, включая по одному фонарику на одинаковое короткое время в некоторой последовательности. Количество вспышек в одном сообщении – 3 или 4, между сообщениями – паузы. Сколько различных сообщений могут передавать мальчики?

Слайд 45

Описание слайда:

Задача 4 Для кодирования 300 различных сообщений используются 5 последовательных цветовых вспышек. Вспышки одинаковой длительности, для каждой вспышки используется одна лампочка определенного цвета. Лампочки скольких цветов должны использоваться при передаче (укажите минимально возможное количество)?

Слайд 46

Описание слайда:

Задача 5 Сколько существует четырехзначных чисел, в записи которых все цифры различны?

Слайд 47

Описание слайда:

Задача 6 Виктор хочет купить пять разных книг, но денег у него хватает только на три (любые) книги. Сколькими способами Виктор может выбрать три книги из пяти?

Слайд 48

Описание слайда:

Задача 7 Цепочка из трех бусин формируется по следующему правилу: На первом месте в цепочке стоит одна из бусин А, Б, В. На втором – одна из бусин Б, В, Г. На третьем месте – одна из бусин А, В, Г, не стоящая в цепочке на первом или втором месте. Сколько всего есть таких цепочек?