🗊Презентация Основы расчета трубопроводов. Гидравлика

Основы расчета трубопроводов

Основы расчета трубопроводов Трубопроводы широко применяются для перемеще­ния жидкостей (вода, нефть, бензин, различные растворы и т. д.) и изготавливаются из металла, бетона, дерева, пластмасс. По степени заполнения поперечного сечения жидкостью различают напорные и безнапорные трубопроводы. В напорных трубопроводах жидкостью заполнено полностью все поперечное сечение; в безнапорных – часть поперечного сечения н имеется свободная поверхность. По соотношению видов потерь напора выделяют короткие и длинные трубопроводы. Короткие трубопроводы – это такие трубопроводы, у которых местные потери напора соизмеримы с потерями напора по длине. К ним относятся бензо- и маслопроводы, всасываю­щие трубопроводы насосных станций, обвязка эксплуатационных нефтяных скважин, сифоны и т. д. Длинные трубопроводы – это трубопроводы, у кото­рых местные потери напора незначительны и не превышают 5-10% от потерь напора по длине, к ним относятся водо­проводы, участки магистральных нефтепроводов. При расчете длинных трубопроводов находят потери напора по длине hл, затем увеличивают их на 5-10%. По конструкции длинные трубопроводы разделяют на простые и сложные. Простые трубопроводы выполняют без ответвлений; сложные изготавливаются с ответвлениями, переменной длины и диаметра и могут соединяться как последовательно, так и параллельно. Сложные трубопроводы образуют тупиковую (незамкнутую) и кольцевую (замкнутую) распределительную сеть. В тупиковой сети жидкость движется в одном направлении. В кольцевой сети жидкость в заданную точку может подаваться по нескольким линиям.

Для расчета простого короткого трубопровода при установившемся истечении жидкости в атмосферу составим уравнение Бернулли для сечений 1–1 и 2–2 (скорости v1 и v2 взяты в соответствующих сечениях): Для расчета простого короткого трубопровода при установившемся истечении жидкости в атмосферу составим уравнение Бернулли для сечений 1–1 и 2–2 (скорости v1 и v2 взяты в соответствующих сечениях): z1+p1/ + v12/(2g)= z2+p2/  + v22/(2g)+hw Обозначая z1-z2 =H (действующий напор) и пренебрегая cкоростным напором в резервуаре v12/(2g), так как он мал по cравнению v22/(2g), получим H= v22/(2g)+hw. Т.о., действующий напор при истечении в атмосферу расходуется на создание кинетической энергии потока на выходе и на преодоление потерь напора, которые складываются из потерь по длине и местных потерь hw=(λl/d+)* v2/2g. В результате подстановки формула примет вид (индекс «2» при скорости v опущен) H= v2/2g (1+ λl/d+).

Составим уравнение Бернулли для трубопровода, в котором жидкость изливается из левого резервуара в правый подуровень Составим уравнение Бернулли для трубопровода, в котором жидкость изливается из левого резервуара в правый подуровень z1+p1/ + v12/(2g)= z2+p2/  + v22/(2g)+hw Пренебрегая скоростными напорами в резервуарах v12/(2g) и v22/(2g), и обозначая z1 – z2 = H, получаем H= h w =v2/2g ( λl/d+), где v – скорость в трубопроводе. В этом уравнении нужно учесть коэффициент потерь напора на выход hм, определяя потери на расширение потока по теореме Борда: hм=( v1-v2)2/2g Принимая v2=0, получаем hл=v2/2g =вых(v2/2g), где вых=1. Тогда, выводя из-под знака суммы вых=1, запишем в виде: H= v2/2g (1+ λl/d+).

При расчете длинных трубопроводов местными сопротивлениями и скоростным напором на выходе пренебрегают и уравнение приобретает вид: При расчете длинных трубопроводов местными сопротивлениями и скоростным напором на выходе пренебрегают и уравнение приобретает вид: H=h л= λl/d *v2/2g Т.е. напор в трубопроводе равен сумме потерь напора по длине, определяемых по формуле Дарси-Вейсбаха. Запишем формулу относительно скорости в трубопроводе, подставив в нее диаметр трубы, выраженный через гидравлический радиус d = 4R, и гидравлический уклон i=hл /l. v= * , обозначив С= , получим формулу Шези v=С * . Расход в трубопроводе определяется по формуле: Q=vw=wC .

Произведение wC обозначают буквой К и называют расходной характеристикой трубопровода, тогда уравнение имеет вид Q=K . Размерность К такая же, как и расхода. Численно значение равно расходу при уклоне, равном единице. Величина 1/K2 = А называется удельным сопротивлением. Потери напора по длине с помощью этих параметров выражаются hл=AlQ2=lQ2/K2.

Типы задач при расчете трубопроводов

При расчете трубопровода возможны три основные постановки задачи. Задача 1 типа. При известном диаметре (d), длине (L), и заданном расходе (Q) требуется определить необходимый напор (Н). При решении использовать уравнение H= v2/2g (1+ λl/d+). Скорость v выражается через расход v=4Q/pd2, тогда Н=16Q2/(2p2d4g)* (1+ λl/d+).

Задача 2 типа. Зная действующий напор и параметр провода, необходимо определить расход. Решая уравнение Н=16Q2/(2p2d4g)* (1+ λl/d+). относительно Q, находим Q=pd2/4*/(1+ λl/d+)=w m=1/.

Задача 3 типа. Зная действующий напор, расход и длину трубопровода, следует определить диаметр трубопровода. Для нахождения диаметра решаем относительно d уравнение Н=16Q2/(2p2d4g)* (1+ λl/d+). Напор в этом уравнении имеет сложную зависимоcть от диаметра. Задача решается обычно или путем подбора, или графоаналитически. При решении графоаналитическим методом, подставляя различные значения диаметров в формулу, получают различные значения напора Н, затем по полученным данным строят график зависимости Η от d. Отложив по оси Н заданный действующий напор, проецируют его на кривую зависимости, а затем точку с кривой на ось d получают искомый диаметр.

Частные случаи расчета трубопроводов

Расчет последовательно соединенных трубопроводов Полученное уравнение позволяет решить 1 тип задач – по известным расходам, длинам и диаметрам участков вычислить напор. Если заданы напор, диаметры, длины участков, то можно вычислить расход (2 тип задач) Задачу 3 типа при помощи уравнения решить нельзя, так как невозможно определить все диаметры участков при известных прочих данных, так как количество неизвестных п, а уравнение одно. Задавшись диаметрами всех участков, кроме одного, последний можно определить, вычислив его расходную характеристику.

Расчет параллельно соединенных трубопроводов Параллельно соединенные трубопроводы относятся к сложным системам. Схема параллельно соединенного трубопровода представлена на рис.. Пусть в точке A трубопровод разветвляется, а в точке В его ветви сходятся. Длина и диаметр каждой ветви соответственно обозначены l1, l2,... ln+1 и d1, d2,... dn+1. Потери напора в каждой ветви одинаковы и равны H=hw, так как концы ветвей смыкаются в точках А к В, в каждой из которых может быть только один напор; кроме того, сумма расходов отдельных ветвей равна магистральному или общему расходу. Исходя из этого, напишем расчетные уравнения для потери напора: для первой ветви hw = Q 12 l1 /K12  для второй ветви hw = Q 22l2 /K22  для n-й ветви hw = Q n2 ln /Kn2  Получается всего n уравнений, в которых содержитcя n+1 неизвестных, в том числе n неизвестных расходов плюс потери напора hw. Чтобы найти все неизвестные, надо иметь еще одно уравнение. Напишем уравнение неразрывности для угловых точек А или В т. е. Q=Q1 +Q2 +…+Qn Имея n+1 уравнений, можно определить все неизвестные. Расходы определяются по отдельным ветвям в соответствии с зависимостью Q1/Q2=K1/K2 =. Отсюда Q2=Q1 , Qn=Q1 , Тогда Q1=Q/(1+ +…+ ).

Расчет трубопроводов при непрерывном изменении расхода по пути В сложных трубопроводах различают расходы: транзитный, передаваемый по магистрали, и путевой (или попутный), отбираемый по пути движения жидкости. Расход называют сосредоточенным, если точки отбора находятся на значительном расстоянии друг от друга, и непрерывным, если эти точки расположены очень близко друг другу. Понятие “непрерывный расход” обычно используют при расчете водопроводных сетей. При непрерывной раздаче жидкости по пути, т.е. в тех случаях, когда жидкость из трубопровода расходуется во многих точках, потерю напора определяют по формуле H=Q02l/(3K2)=AlQ02/3, где Q0 – начальный расход, непрерывно и равномерно расходуемый по длине трубы. Если часть расхода по трубе проходит транзитом Qтр, а часть расходуется непрерывно и равномерно cоставит по длине трубы Q0, общая потеря напора Н= l /K2*(QА2 - QАQ0 +Q02/3) , где QА – начальный общий расход в трубе QА= Qтр+ Q0

Расчет разветвленного трубопровода Тупиковый трубопровод, показанный на рис., состоит из магистрального трубопровода l, питаемого от резервуара А, и двух ответвлений 2 и 3, в конце которых в точках С и D происходит отбор расхода жидкости, вытекающей в атмосферу. Основными задачами при гидравлическом расчете разветвленной сети можно считать определение концевых расходов Q2 и Q3 при заданном напоре H в начальном сечении или определение потерь напора при заданных концевых расходах Q2 и Q3. В качестве примера рассмотрим первую задачу. Так как участки 1 и 2 соединены последовательно, то суммарные потери напора на участке А С равны H=H1+H2. Аналогично для участков 1 и 3 на пути AD имеем H=H1+H3. Учитывая формулу H= AlQ2, эти уравнения можно переписать в виде: H=A1l1Q12+A2l2Q22; (1) H=A1l1Q12+A3l3Q32. (2) Вычитая из первого уравнения второе, получим A2l2Q22=A3l3Q32. (3 ) Так как участки 2 и 3 имеют в начале общую точку В, а истечение жидкости из точек С и D происходит в атмосферу, то можно считать, что участки 2 и 3 соединены параллельно, следовательно Q1=Q2+Q3. ( ) Из равенства (3) следует, что Q3=Q2. (4) Подставляя последнюю формулу в равенство (Q1=Q2+Q3), получим Q1=Q2 (1+ ) С учетом этого равенства по уравнению (1) определяется концевой расход Q2, при заданном напоре Н, а расход Q3 определяется по формуле (4)

В том случае, если точки С и D расположены в разных горизонтальных плоскостях, то аналогичная система уравнений получает вид: В том случае, если точки С и D расположены в разных горизонтальных плоскостях, то аналогичная система уравнений получает вид: za – zс = A1l1Q12+A2l2Q22, za – zD =A1l1Q12+A3l3Q32. Откуда zс +A2l2Q22= zD +A3l3Q32. Кроме того, имеем Q1=Q2+Q3. Решая эти уравнения аналогично изложенному выше, находим концевые расходы Q2 и Q3. Обычно требуется определить диаметр прокладываемых труб и высоту водонапорной башни. Для этого по заданным расходам Q1, Q2 и Q=Q1+Q2 и допускаемым скоростям в трубах рассчитывается диаметр труб. Затем по принятому диаметру труб определяются потери напора на участках ответвлений и на магистральном участке. Далее потери напора на том ответвлении, где они имеют большее значение, суммируются с потерями напора на магистральном участке и таким образом, находятся общие потери, а по ним из уравнений с учетом геометрических высот можно определить и высоту башни.

Расчет кольцевого трубопровода Таким образом, расчет кольцевого трубопровода сводится к следующему. Прежде всего задаются направлением движения жидкости и назначают точку схода, затем пользуясь таблицами, определяют потери напора по участкам сети. Если точка схода была назначена правильно, то сумма потерь напора в полукольцах должна быть одинакова. h2 + h3 = h4. Разница в потерях напора по полукольцам (невязка) допускается не более 5% суммы потерь напора по длине полукольца. Если указанное условие не выполняется, следовательно, точка схода назначена неверно, и ее переносят в ту сторону, где потери оказались больше. Методом повторных попыток добиваются равенства потерь.

Расчет сифона Составим уравнение Бернулли для сечений 1–1 и 2–2, взяв за плоскость отсчета плоскость 0–0, совпадающую с 2–2: H+pат/g+ v12/(2g)= 0+ pат/g + v22/(2g)+hw. Пренебрегая скоростными напорами в резервуарах, получаем H= hw= v2/2g*(1+ λ*l /d+ ) где v – скорость движения воды в сифоне; Σ λ – сумма коэффициентов сопротивлений по длине на восходящем, на горизонтальном и на нисходящем участках. Если диаметр на всех участках сифонной трубы один и тот же, то λ *l /d = λl/d, где l – длина сифонной трубы. Тогда получим уравнение H= v2/2g*(1+ λl/d+ ), где  – сумма коэффициентов местных сопротивлений =вх+вых+2пов. Полученное уравнение может быть решено относительно любого из трех неизвестных: Н, v (Q), d, т. е. сифонный трубопровод может быть рассчитан в любой постановке задачи.

Однако при расчете сифона надо дополнительно убедиться возникнет ли в трубе чрезмерный вакуум, так как глубокий вакуум· может вызвать вскипание жидкости, что нарушит работу сифона.·Составим уравнение Бернулли для сечений 1–1 и x-x относительно плоскости 0–0 Однако при расчете сифона надо дополнительно убедиться возникнет ли в трубе чрезмерный вакуум, так как глубокий вакуум· может вызвать вскипание жидкости, что нарушит работу сифона.·Составим уравнение Бернулли для сечений 1–1 и x-x относительно плоскости 0–0 H+pат/g + v12/(2g)= Н +z+px/g + v22/(2g)+hw . Полагая v1=0, перепишем уравнение (pат –px)/g = z +v2/(2g) +( λl/d+)*v2/(2g). Величина в левой части уравнения представляет собой вакуум hвак= (pат –px)/g, и hвак= z +(1+ λl/d+)*v2/(2g), где v – скорость движения воды в сифоне; z – высота в сечении х–х над уровнем воды в резервуаре, l – части сифонной трубы от начала до сечения x–x сечения,  - сумма коэффициентов местных сопротивлений от начала трубы до сечения x–x. В нашем случае  =вх+пов. Из уравнения следует, что hвак будет тем больше, чем больше z, скорость v и потери напора.

Pасчет всасывающего трубопровода насоса Pасчет всасывающего трубопровода насоса – участка трубопровода от места водозабора до насоса, ведется аналогично расчету сифона. Определяется вакуум во всасывающем трубопроводе перед входом в насос, для этого составляется уравнение Бернулли для сечений 1-1 и 2-2, принимая плоскость сравнения 0-0 на уровне жидкости в резервуаре: pат/g = z + p2/g + v2/(2g) +( λl/d+)*v2/(2g), где z – высота установки насоса, называемая геометрической высотой всасывания. Это уравнение показывает, что процесс всасывания, т.е. подъем жидкости на высоту z, сообщение ей скорости и преодоление всех гидравлических сопротивлений, происходит в результате использования, (с помощью насоса) атмосферного давления. Из формулы можно получить выражение для вакуумметрической высоты всасывания: hвак= (pат –p2)/g= z + v2/(2g) +( λl/d+)*v2/(2g). Из этой формулы видно, что для уменьшения вакуума на входе в насос необходимо уменьшать высоту установки насоса, скорость движения жидкости и гидравлические сопротивления.

Изменение пропускной способности трубопроводов в процессе их эксплуатации При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается – в некоторых случаях (например, для трубопрово­дов водоснабжения) до 50% расчетной и даже ниже. Вследствие коррозии и инкрустации (образование отложений в трубах) шероховатость труб увеличивается, что в первом приближении можно оценить по формуле  = 0 + t, где  – шероховатость, мм, для новых труб (в начале эксплуатации);  – абсолютная шероховатость, мм, через t лет эксплуатации; – коэффициент, характеризующий быстроту возрастания шероховатости, мм/год. Значение коэффициента α зависит от материала труб и свойств жидкости. В табл. приведены значения α (по А.Д. Альштулю и А.Г. Камерштейну) в зависимости от физико-химических свойств транспортируемой воды.

Гидравлический удар Изменение давления в водоводах, вызванное резким увеличением или уменьшением скорости движения жидкости, называется гидравлическим ударом. Гидравлический удар в 1898 г. подробно описал выдающийся русский ученый Η. Ε. Жуковский. Ударное давление Δρ определяется разностью давлений при неустановившемся и установившемся режимах. Если давление Δρ>0 то удар называется положительным, при Δρ<0 то отрицательным.

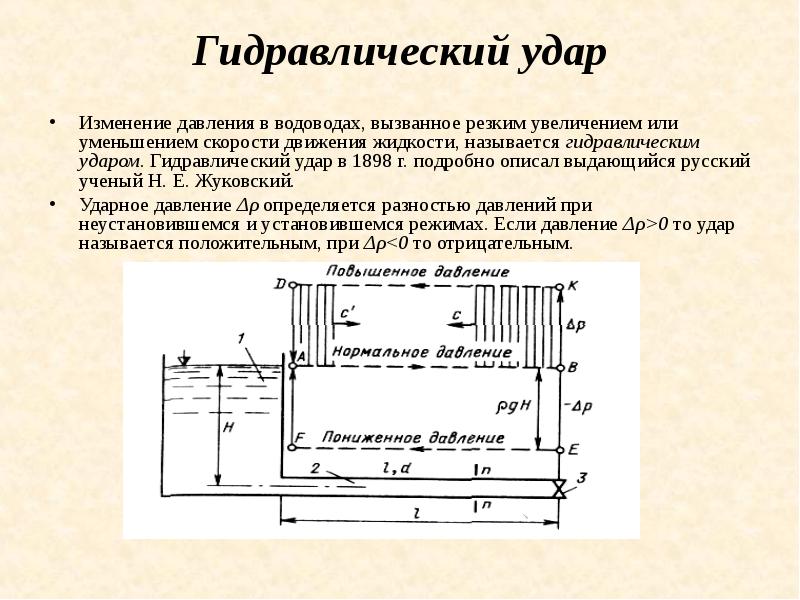
Различают четыре этапа развития гидравлического удара. Первый этап. Допустим, что задвижка 3 мгновенно закрылась и слой жидкости, находящийся у задвижки остановился, а вся жидкость в трубе 2 продолжает двигаться с прежней скоростью v. Через некоторое время начнут останавливаться и другие слои жидкости слева от задвижки, т.е. фронт остановившейся жидкости будет перемещаться от задвижки к резервуару 1. Обозначим этот фронт сечением n–n. В остановившемся объеме между задвижкой сечением возникает дополнительное давление Δρ. Итак, слева от сечения n–n жидкость движется вправо со скоростью v и в трубе будет прежнее давление р; справа от сечения n–n; жидкость неподвижна и давление равно p+Δp. Фронт сжатия быстро перемещается в сторону резервуара. Скорость перемещения этого фронта называется скоростью распространение ударной волны c. Описанный процесс будет продолжаться до тех пор, пока волна не дойдет до резервуара. Этим заканчивается первый этап гидравлического удара, в конце этого этапа вся жидкость в трубе неподвижна, сжата и находится под давлением p+Δp. Некоторый дополнительный объем жидкости из резервуара поступит в трубу. Различают четыре этапа развития гидравлического удара. Первый этап. Допустим, что задвижка 3 мгновенно закрылась и слой жидкости, находящийся у задвижки остановился, а вся жидкость в трубе 2 продолжает двигаться с прежней скоростью v. Через некоторое время начнут останавливаться и другие слои жидкости слева от задвижки, т.е. фронт остановившейся жидкости будет перемещаться от задвижки к резервуару 1. Обозначим этот фронт сечением n–n. В остановившемся объеме между задвижкой сечением возникает дополнительное давление Δρ. Итак, слева от сечения n–n жидкость движется вправо со скоростью v и в трубе будет прежнее давление р; справа от сечения n–n; жидкость неподвижна и давление равно p+Δp. Фронт сжатия быстро перемещается в сторону резервуара. Скорость перемещения этого фронта называется скоростью распространение ударной волны c. Описанный процесс будет продолжаться до тех пор, пока волна не дойдет до резервуара. Этим заканчивается первый этап гидравлического удара, в конце этого этапа вся жидкость в трубе неподвижна, сжата и находится под давлением p+Δp. Некоторый дополнительный объем жидкости из резервуара поступит в трубу. Второй этап. Начало второго этапа совпадает с окончанием первого. Сжатая жидкость расширяясь, начнет двигаться в сторону резервуара. Сначала придут в движение слои жидкости вблизи резервуара, а затем и более отдаленные, т.е. фронт спада давления n–n начнет повышаться от резервуара к задвижке. К концу фазы вся жидкость в трубе движется со скоростью υ в сторону резервуара давление в трубе восстанавливается до первоначального. Третий этап. Начало третьего этапа характеризуется тем, что жидкость в трубе движется в сторону резервуара со скоростью v. У задвижки возникает слой жидкости, в котором давление на Δр меньше первоначальною. Теперь фронт n-n пониженного давления перемешается в сторону резервуара слева от него давление р, скорость направлена влево, справа жидкость неподвижна, давление в ней на Δρ ниже нормального, Третий этап заканчивается приходом фронта n–n к резервуару. Четвертый этап. Начало четвертого этапа характеризуется тем, что давление у входа в трубу со стороны резервуара р, а со стороны трубы меньше на Δp, т.е. р–Δp . Такое неуравновешенное состояние приведет к тому, что жидкость из резервуара начнет втекать в трубу со скоростью v и в ней будет повышаться до р.

Рассмотрим слой жидкости от задвижки до сечения n-n длиной Δl и площадью поперечного сечения w. Остановившаяся масса жидкости (m) в этом объеме потеряла количество движения за время Δt, в течение которого фронт повышенного давления передвинулся от задвижки влево на расстояние Δl: Рассмотрим слой жидкости от задвижки до сечения n-n длиной Δl и площадью поперечного сечения w. Остановившаяся масса жидкости (m) в этом объеме потеряла количество движения за время Δt, в течение которого фронт повышенного давления передвинулся от задвижки влево на расстояние Δl: mv=w Δlv. Импульс силы за тот же промежуток времени равен ΔpwΔt. Справа от сечения n–n давление p + Δp. слева от него – р. Произведение Δρw есть сила, остановившая объем жидкости w Δl за время Δt. Приравняв импульс силы к количеству движения получим ΔpwΔt=w Δlv. Откуда Δp= Δlv/Δt, где v скорость в трубопроводе до закрытия задвижки и поскольку Δl/Δt – скорость распространения ударной волны c, запишем Δp= сv. Эта формула была впервые получена Η.Е. Жуковским.

В реальных условиях процесс гидравлического удара протекает несколько иначе, так как при 6ольших давлениях, сопровождающих гидравлический удар, сказывайся как сжимаемость жидкости, так и упругость стенок водовода. Для случая упругих стенок Η.Ε. Жуковским была получена также формула для определения скорости ударной волны. В реальных условиях процесс гидравлического удара протекает несколько иначе, так как при 6ольших давлениях, сопровождающих гидравлический удар, сказывайся как сжимаемость жидкости, так и упругость стенок водовода. Для случая упругих стенок Η.Ε. Жуковским была получена также формула для определения скорости ударной волны. c= где  – плотность жидкости; d – внутренний диаметр трубы, d – толщина стенок трубы; Eж – модуль упругости жидкости (кг/м2), Етр – модуль упругости материала стенок трубы. Если труба абсолютно жесткая Етр∞, то с0=Eж/r, тогда скорость распространения ударной волны с0 при абсолютно жестких стенках трубопровода равна скорости распространения звука в воде (с0=1425 м/с) и для воды: с=1425/ Формула справедлива для так называемого прямого удара, т.е. когда время закрытия задвижки меньше фазы удара tз<T (T=2L/c, где L – длина трубопровода от места его перекрытия до сечения в котором давление считается постоянным). Если tз>T удар называют непрямым, и ударное повышение давления Δp будет меньше определяемого по формуле. При таких условиях повышение давления можно найти по формуле Мишо Δp= сv(T/tз)= При условии, что tз=T результаты расчетов по этим формулам одинаковы.

Источники: