🗊Презентация Спектральные представления

IV. Спектральные представления

13. Преобразование Фурье Преобразование Фурье — операция, сопоставляющая сигналу от вещественной переменной - времени другую функцию (возможно комплекснозначную) от вещественной переменной - частоты. Эта новая функция описывает часто-ты, которые образуют исходный сигнал. Формула дискретного преобразования Фурье (ДПФ):

13. Преобразование Фурье Обратное преобразование Фурье может быть получено из формулы для прямого преобразования

13. Преобразование Фурье Будем рассматривать дискретные линейные системы, то есть системы, работающие с дискретными сигналами. На вход такой системы подается последовательность чисел x[n] – это дискретный сигнал, на выходе получается последовательность чисел y[n]. x[n]

13. Преобразование Фурье Дельта-функция (цифровая) – это сигнал вида

13. Преобразование Фурье Пример

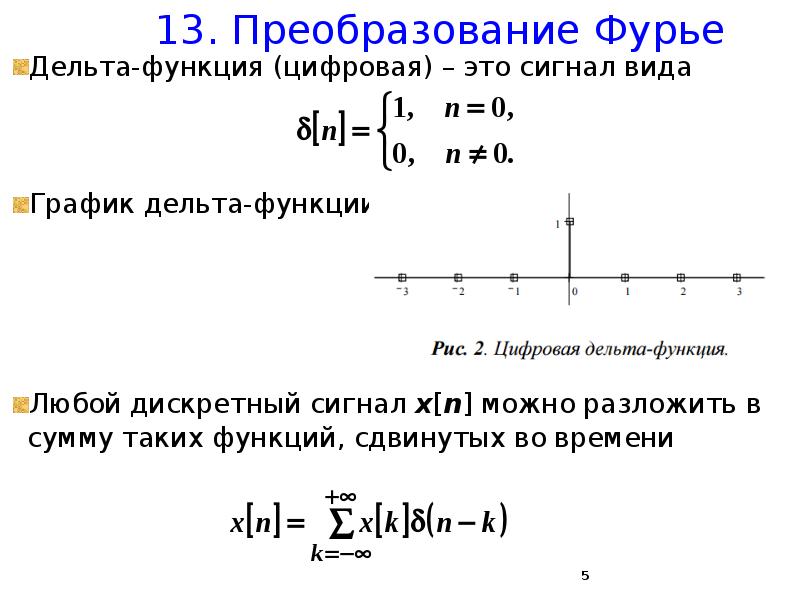
13. Преобразование Фурье Пусть линейная система преобразует некоторый сигнал x[n]. Подадим дельта-функцию на вход системы и измерим выходной сигнал. Пусть δ[n] →h[n] , то есть получили отклик на дельта-функцию. Оказывается, что зная h[n] (отклик системы на дельта-функцию), можно вычислить отклик системы на любой входной сигнал. Действительно, так как любой входной сигнал является линейной комбинацией сдвинутых во времени дельта- функций, то выходной сигнал будет той же самой линей-ной комбинацией сдвинутых во времени функций h[n]. Формула для вычисления выходного сигнала y[n] по входному сигналу x[n] такова:

13. Преобразование Фурье Пусть задан сигнал h(n) – отклик на дельта-функцию

13. Преобразование Фурье

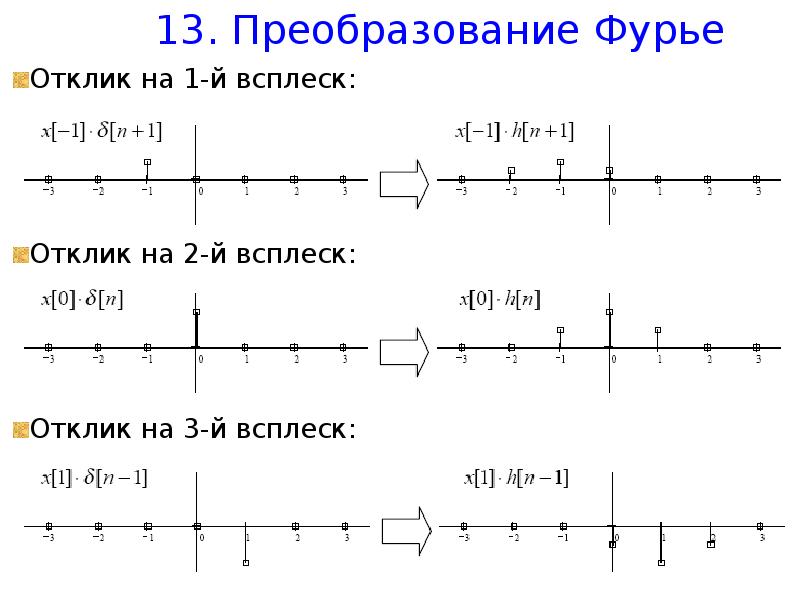
13. Преобразование Фурье Сумма трех всплесков дает дискретный сигнал, который и будет откликом на вход x[n] Он напоминает синусоиду.

13. Преобразование Фурье Сигнал h[n] называется импульсной характеристикой системы, т.к. он является откликом системы на единичный импульс (дельта-функцию). Рассмотрим алгоритм вычисления отклика линейной системы на произвольный сигнал для изображения. Дискретное изображение – это двумерный сигнал x[i,j], обозначающий яркость изображения в каждой дискретной точке (пикселе) (i,j) на плоскости. Дельта-функция в двумерном случае – это единичная светлая точка с координатами (0,0) на черном фоне. Пусть наша линейная система отвечает на дельта-функцию функцией h[i,j], такой что h[i,j]=const на всех точках внутри круга с центром в точке (0,0) и диаметром 3 и равна нулю вне этого круга. При этом интеграл от h[i,j] по всей плоскости равен 1 (из этого условия выбираем константу const).

13. Преобразование Фурье Рассмотрим действие такой системы на изображение, состоящее из одной точки на черном фоне, но пусть теперь точка имеет координаты (m, n) и в эту точку сдвинута дель-та-функция δ[i − m, j − n] . Тогда откликом системы будет изображением h[i-m, j-n]. Таким образом, на единичные всплески в любой точке изображения система отвечает кругом радиуса 3 с центром в этой точки. То есть точка как бы размывается в круг. Поэтому в ком-пьютерной графике импульсную характеристику линейной системы называют PSF – point spread function, т.е. функция размытия точки.

13. Преобразование Фурье Дискретная свертка. Формула свертки для одномерного случая:

13. Преобразование Фурье Пусть дискретный сигнал x[n] имеет период N точек. В этом случае его можно представить в виде конечного ряда (т.е. линейной комбинации) дискретных синусоид:

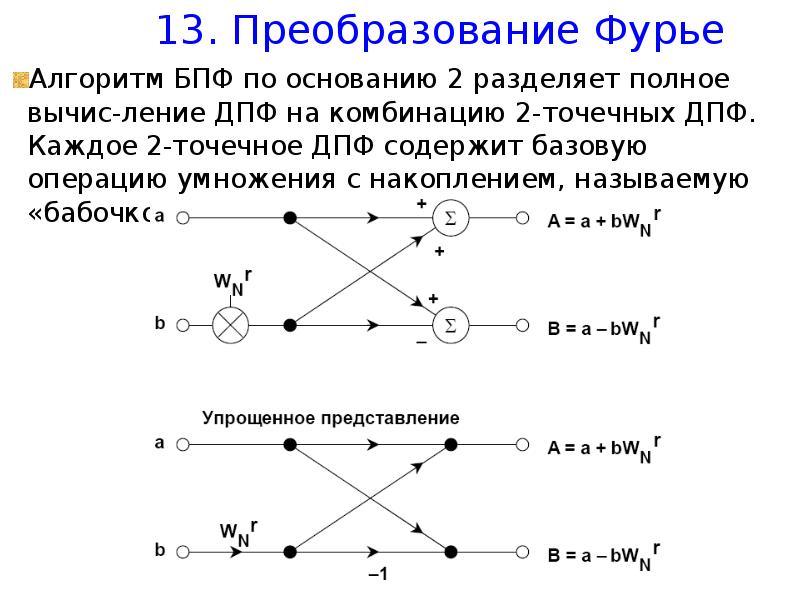
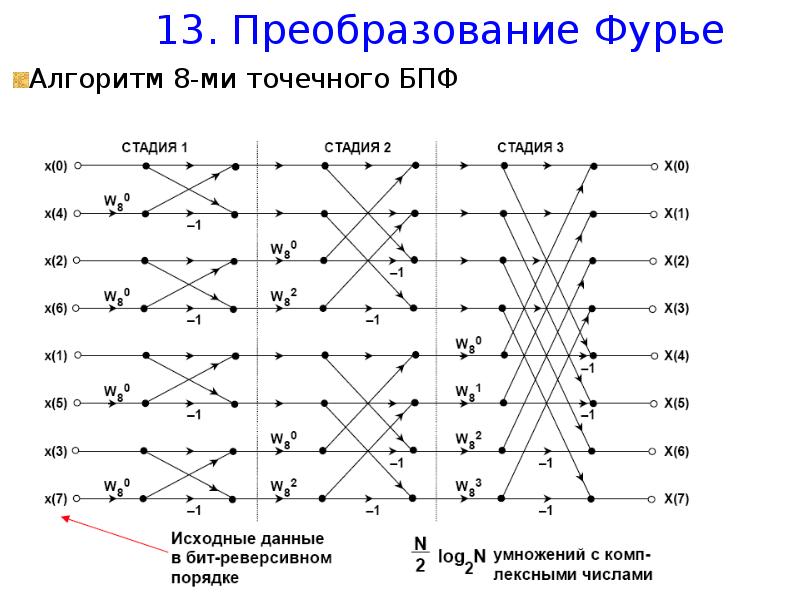
13. Преобразование Фурье Самое известное в цифровой обработке сигналов преоб-разование из временной области в частотную – это дискрет-ное преобразование Фурье (ДПФ). Аргументом является дискретная по времени выборка периодического сигнала во временной области, при этом сигнал должен быть определен на оси времени от -∞ до +∞. Но реально набор входных данных для ДПФ – это конечное число отсчетов, обозначим их количество N . Эту проблему можно решить, повторяя бесконечное число раз эти N отс-четов, чтобы обеспечить периодичность. Таким образом, реально N -точечное ДПФ преобразует дискретный сигнал x[n] , заданный на N точках. Виртуаль-но от периодический, и период его самое большее, равен интервалу, на котором лежат эти N точек.

13. Преобразование Фурье Преобразование имеет два представления, экспоненциа-льное и тригонометрическое, которые эквивалентны:

13. Преобразование Фурье

13. Преобразование Фурье

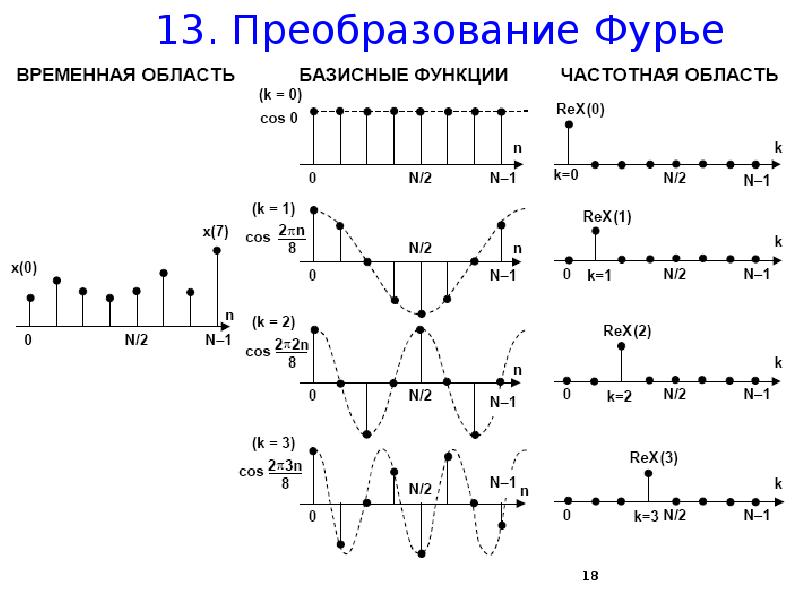
13. Преобразование Фурье Еще пример. Входной сигнал x[n] равен дискретизации функции cos (2π/N). Тогда вещественная часть спектра будет равна:

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье

13. Преобразование Фурье