Описание слайда:
Наибольшее отражение дают слои, толщина которых: hCЛ = λ / θр (град)
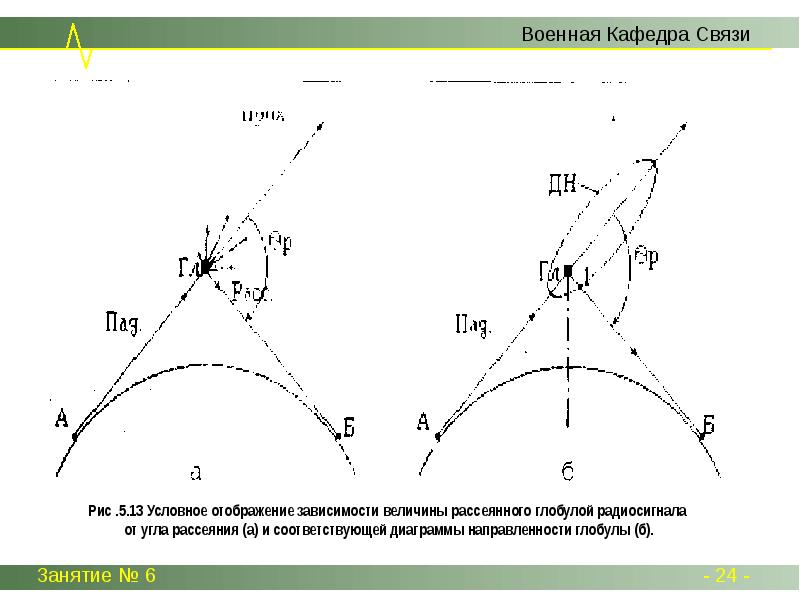
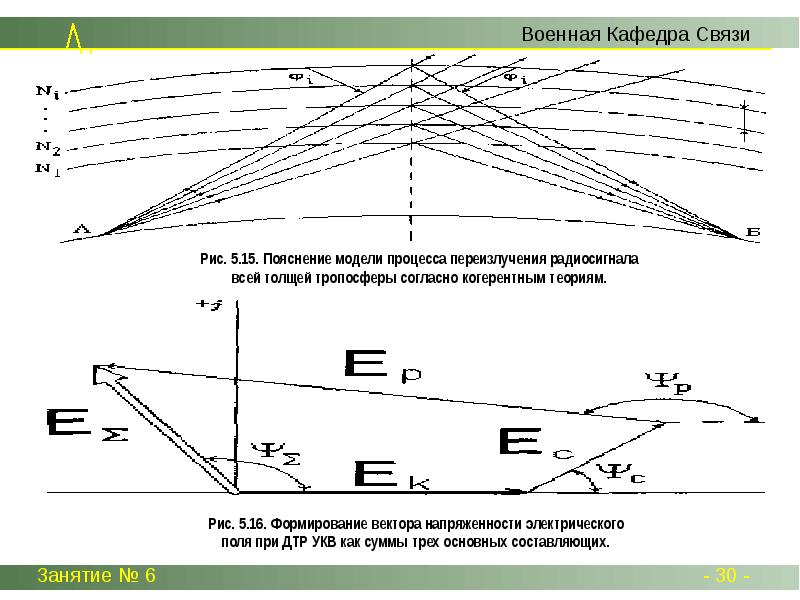
Диаграмма направленности ДН отражения (и рассеяния) волн от слоистых неоднороднос-тей имеет лепесток, направленный под углом φ отр (рис.5.14б). Суммарное электрическое поле в точке Б, обус-ловленное отражением от слоев, может быть представлено вектором Ес, определяемым суммой, по-добной (5.21) . Однако в этом случае число n составляет единицы (или может быть равно нулю), а компоненты Еi - более интенсивны, но также характеризуются случайностью и некоррелированнос-тью модулей и фаз. Интерферентность компоненты Ei, несмотря на неотносительно малую абсолют-ную и относительную подвижность слоев, может приводить к существенным и быстрым изменениям модуля и фазы вектора Ес, что объясняется относительной малостью длин волн (дециметры, санти-метры). Рассеяние волн глобулами и отражение волн слоями характеризуется многолучевостью, при которой фазовые углы компоненты Еi случайны и практически некоррелированы. Поэтому теории ДТР УКВ, основанные на учете рассмотренных механизмов, получили название некогерентных. Про-цесс отражения волн всей толщей тропосферы поясняется с помощью рис. 5.15. Поскольку плот-ность толщи тропосферы монотонно убывает с увеличением высоты, это вызывает диффузное "отражение", т.е. рассеяние волн. Если представить, что вся толща тропосферы разбита на n слоев толщиной Δh и внутри каждого слоя значение индекса преломления Ni постоянно, а на границах сло-ев оно претерпевает скачок на величину ΔN=Nk -Nk+1 , то от границ слоев должны возникать отражен-ные лучи, сходящиеся в точку Б. Из такой модели исходят когерентные теории ДТР УКВ, название ко-торых объясняется постоянством сдвигов фаз между отраженными компо-нентами в точке Б. Реаль-но слои, показанные на рис. 5.15 отсутствуют, т.е. можно предположить, что их число бесконечно, а толщина близка к нулю и, следовательно, число отраженных компонент также бесконечно, а интенсивность их ничтожно мала.