Готовые презентации на тему:
- Образование
- Искусство и Фото
- Наши презентации
- Авто/мото
- Технологии
- Бизнес и предпринимательство
- Карьера
- Данные и аналитика
- Дизайн
- Устройства и комплектующие
- Экономика и Финансы
- Машиностроение
- Развлечения и Юмор
- Путешествия
- Eда
- Политика
- Юриспруденция
- Здоровье и Медицина
- Интернет
- Инвестиции
- Закон
- Стиль жизни
- Маркетинг
- Мобильные технологии
- Новости
- Недвижимость
- Рекрутинг
- Розничная торговля
- Таможня, ВЭД, Логистика
- Наука
- Услуги
- Программное обеспечение
- Спорт
- Музыка
- Шаблоны презентации
- Детские презентации
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- История
- Литература
- Информатика
- Математика
- Обществознание
- Русский язык
- Физика
- Философия
- Химия
- МХК
- ОБЖ
- Окружающий мир
- Педагогика
- Технология
- Начальная школа
- Раскраски для детей
- Товароведение
- Менеджмент
- Страхование


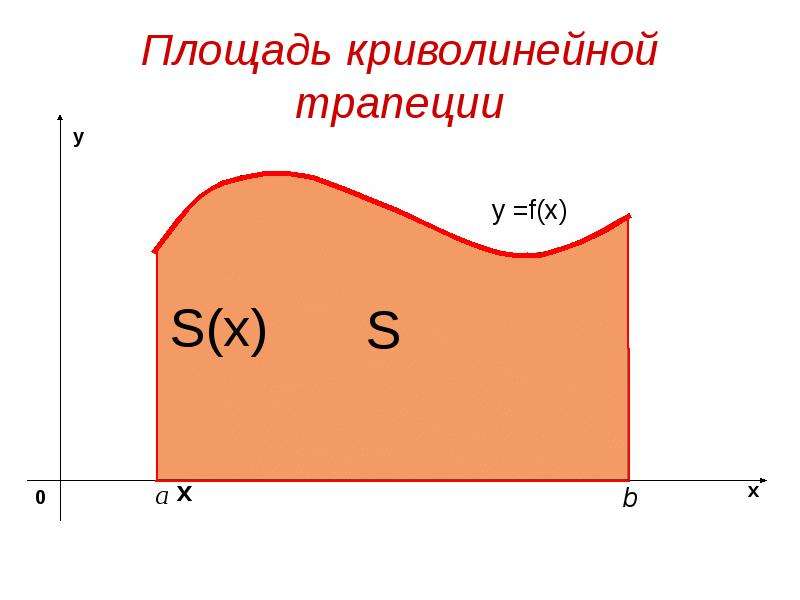
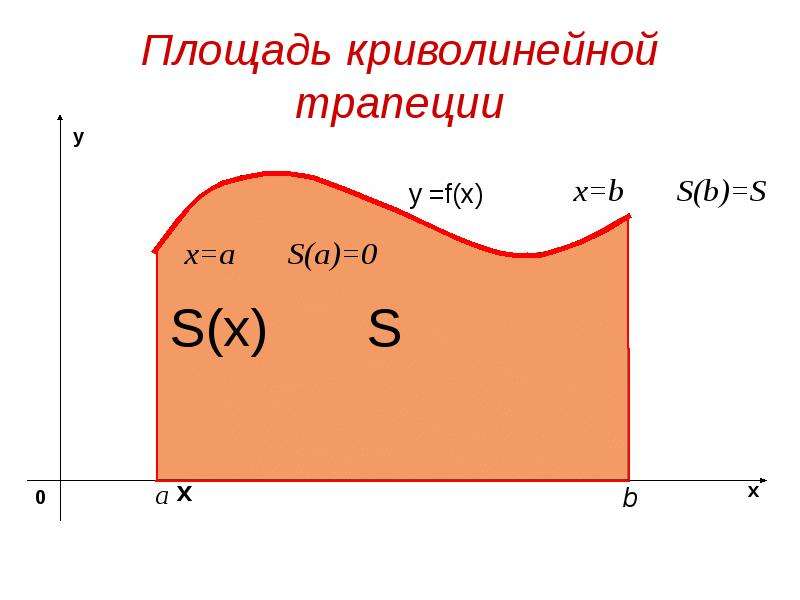

![Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные значения , а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.
Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные значения , а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.](/documents/e5264da345c371daa2a8027e53b04cad/img6.jpg)
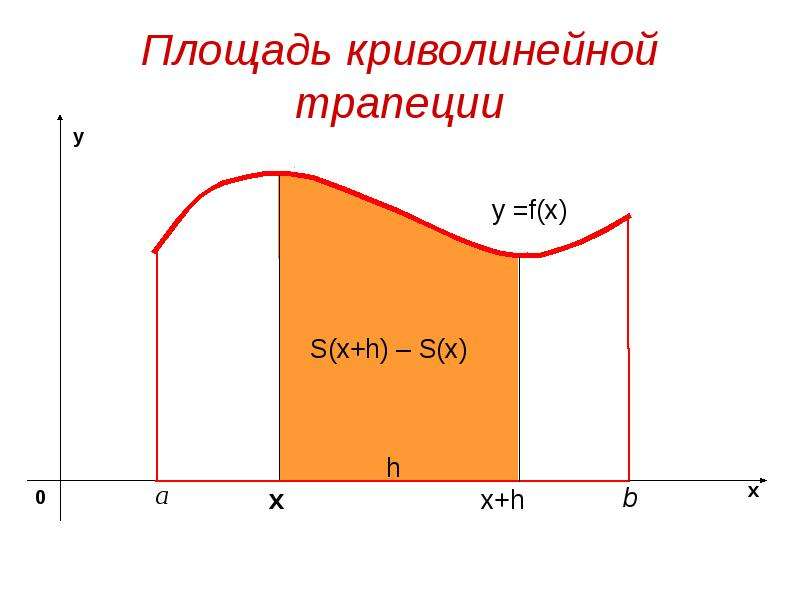
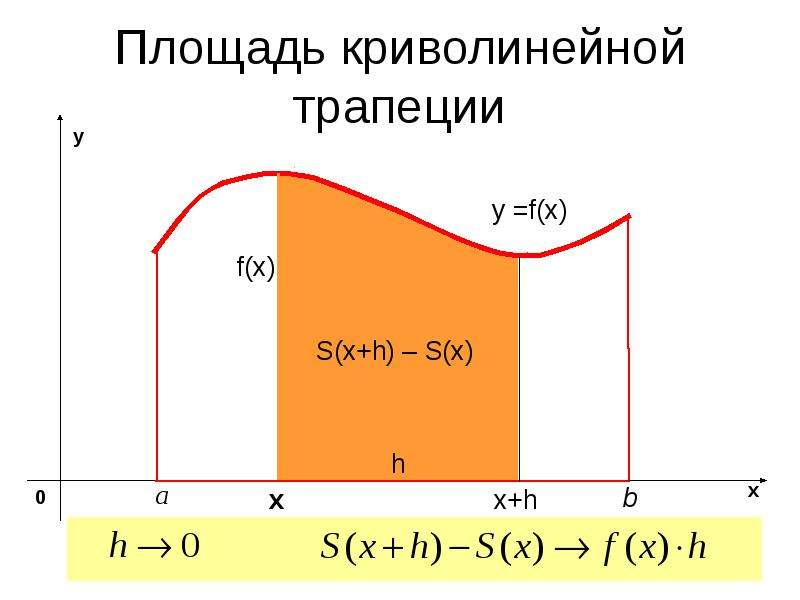
![Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х] ,
Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х] ,
х - любая точка отрезка [a, b]
При х = а отрезок [a, х] вырождается в
точку, поэтому S(а) = 0; при х = b,
S(b) = S](/documents/e5264da345c371daa2a8027e53b04cad/img7.jpg)
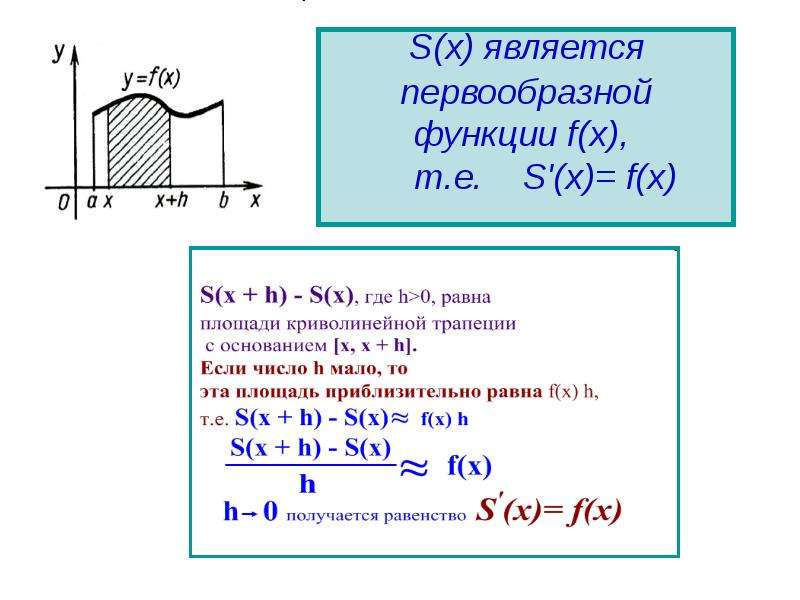
![Площадь криволинейной трапеции
вычисляется по формуле
S = F(b) - F(a)
Разность F(b) - F(a) называют
интегралом от функции f(x)
на отрезке [a, b] и обозначают так :](/documents/e5264da345c371daa2a8027e53b04cad/img9.jpg)