Описание слайда:
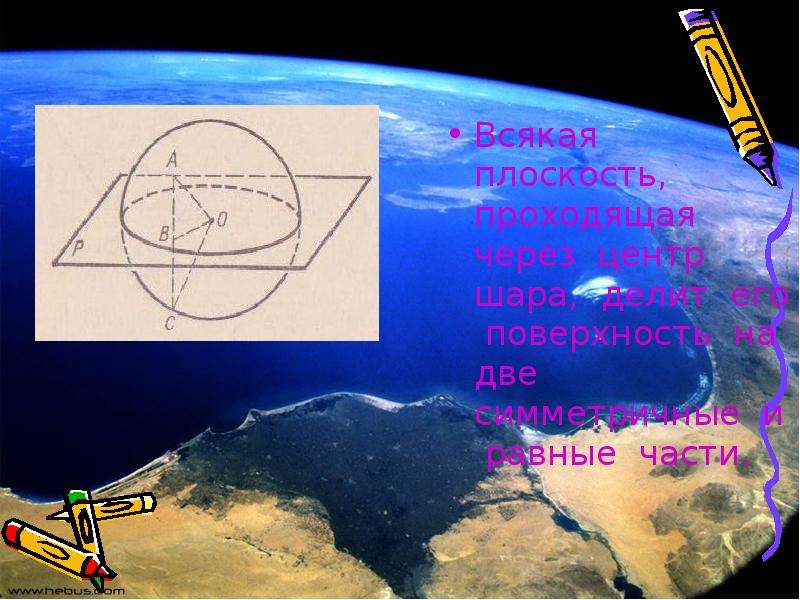
Сферическая геометрия – это геометрическая дисциплина, изучающая свойства фигур, расположенных на сфере. Сферическая геометрия изучает свойства фигур на плоскости. Большие круги на сфере, являясь геодезическими линиями, играют роль прямых на плоскости: через две точки сферы, не совпадающие с концами ее диаметра, проходит только одна большая окружность сферической геометрии аналогично тому, как на плоскости через две различные точки проходит только одна прямая. Однако в сферической геометрии нельзя провести параллельных «прямых», в то время как на плоскости Евклида и плоскости Лобачевского существуют параллельные прямые. Основными фигурами сферической геометрии являются сферические двуугольники, сферические треугольники, сферические многоугольники, т.е многоугольники на сфере, сторонами которых являются дуги больших окружностей, длинна которых меньше длинны полуокружности. Сферу, как и плоскость, можно перемещать по самой себе. Сферическая геометрия одна из простейших геометрий, отличных от обычной геометрии Евклида. В этой геометрии много удивительных фактов, не имеющих места в геометрии Евклида. Сферическая геометрия находит применение в астрономии, в географии, в мореплавании и других науках и областях знаний.
Сферическая геометрия – это геометрическая дисциплина, изучающая свойства фигур, расположенных на сфере. Сферическая геометрия изучает свойства фигур на плоскости. Большие круги на сфере, являясь геодезическими линиями, играют роль прямых на плоскости: через две точки сферы, не совпадающие с концами ее диаметра, проходит только одна большая окружность сферической геометрии аналогично тому, как на плоскости через две различные точки проходит только одна прямая. Однако в сферической геометрии нельзя провести параллельных «прямых», в то время как на плоскости Евклида и плоскости Лобачевского существуют параллельные прямые. Основными фигурами сферической геометрии являются сферические двуугольники, сферические треугольники, сферические многоугольники, т.е многоугольники на сфере, сторонами которых являются дуги больших окружностей, длинна которых меньше длинны полуокружности. Сферу, как и плоскость, можно перемещать по самой себе. Сферическая геометрия одна из простейших геометрий, отличных от обычной геометрии Евклида. В этой геометрии много удивительных фактов, не имеющих места в геометрии Евклида. Сферическая геометрия находит применение в астрономии, в географии, в мореплавании и других науках и областях знаний.