Скачать презентацию Математика на шахматной доске - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Скачать презентацию Математика на шахматной доске, слайд №1

Скачать презентацию Математика на шахматной доске, слайд №2

Скачать презентацию Математика на шахматной доске, слайд №3

Скачать презентацию Математика на шахматной доске, слайд №4

Скачать презентацию Математика на шахматной доске, слайд №5

Скачать презентацию Математика на шахматной доске, слайд №6

Скачать презентацию Математика на шахматной доске, слайд №7

Скачать презентацию Математика на шахматной доске, слайд №8

Скачать презентацию Математика на шахматной доске, слайд №9

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Скачать презентацию Математика на шахматной доске. Доклад-сообщение содержит 9 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Слайд 2

Описание слайда:

Шахматы не только популярная игра, но и источник множества интересных математических задач. Не случайно шахматные термины можно встретить в литературе по комбинаторике , теории графов, кибернетике, теории игр, программированию . Расскажем о нескольких математических задачах на шахматной доске. Шахматы не только популярная игра, но и источник множества интересных математических задач. Не случайно шахматные термины можно встретить в литературе по комбинаторике , теории графов, кибернетике, теории игр, программированию . Расскажем о нескольких математических задачах на шахматной доске. Задача 1. Обойти конем все поля доски, посетив каждое из них по од- ному разу. Этой задачей занимался Л.Эйлер

Слайд 3

Описание слайда:

Слайд 4

Описание слайда:

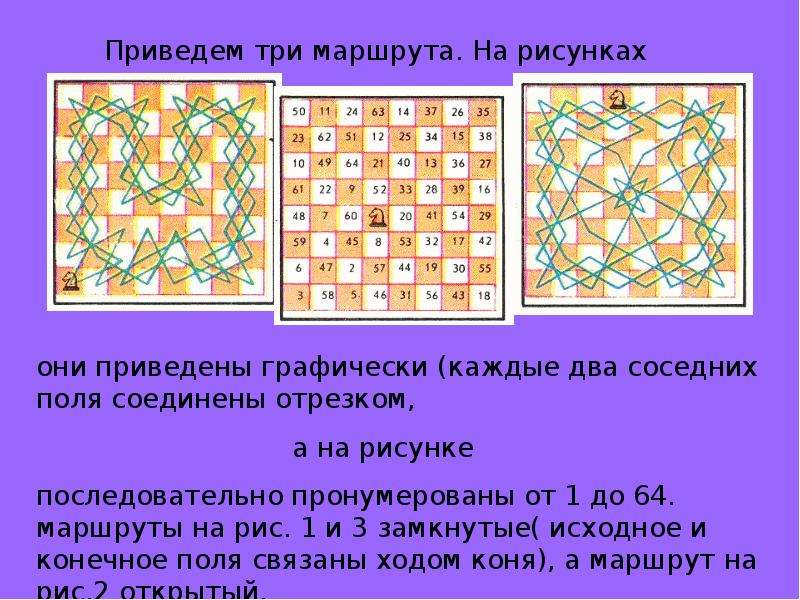
Задачи о маршрутах составлены и для других фигур. Задачи о маршрутах составлены и для других фигур. На рис. изображен кратчайший замкнутый маршрут ферзя по всей доске, занимающий 14 ходов.

Слайд 5

Описание слайда:

Задача 2. Сколькими способами можно расставить на доске 8 ферзей так. Чтобы они не угрожали друг другу (никакие два из их не стояли бы на одной линии) ? Существует 92 требуемые расста- новки (докажите), причем они получаются из 12 основных поворотами и зеркальными отражениями доски. Одно из решений:

Слайд 6

Описание слайда:

Сначала выясняется, какое наибольшее число фигур не угрожает на доске друг другу, а затем- сколько имеется расстановок. Сначала выясняется, какое наибольшее число фигур не угрожает на доске друг другу, а затем- сколько имеется расстановок. Ладей, как и ферзей, можно расставить максимум 8 (всего 8!=40320 расстановок). Максимальное число не угрожа- ющих друг другу слонов равно 14 (256 расстановок), Коней -32, королей- 16 (281571 расстановка).

Слайд 7

Описание слайда:

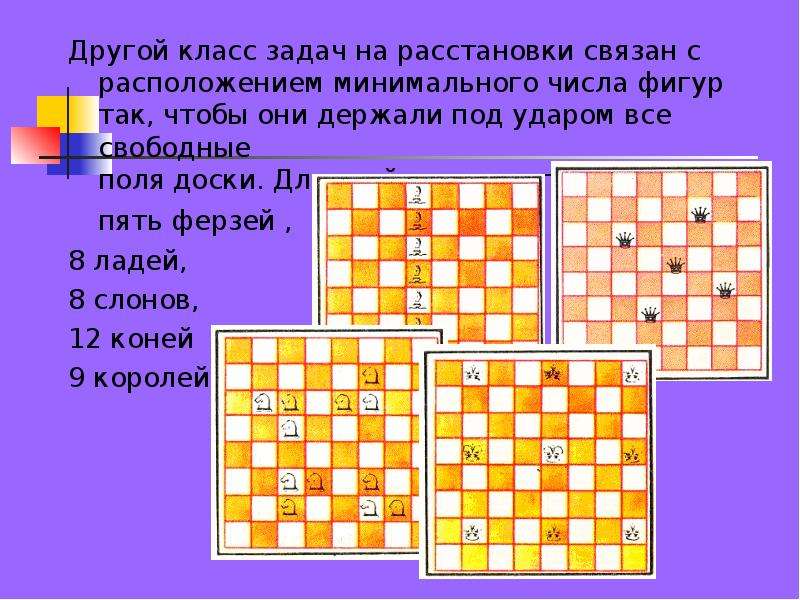
Другой класс задач на расстановки связан с расположением минимального числа фигур так, чтобы они держали под ударом все свободные поля доски. Для этой цели достаточно взять пять ферзей , Другой класс задач на расстановки связан с расположением минимального числа фигур так, чтобы они держали под ударом все свободные поля доски. Для этой цели достаточно взять пять ферзей , 8 ладей, 8 слонов, 12 коней 9 королей

Слайд 8

Описание слайда:

Для охраны доски меньшим, чем пять, числом фигур не обойтись, однако их состав можно «ослабить», заменив двух ферзей ладьями или даже ладьей с королем или Для охраны доски меньшим, чем пять, числом фигур не обойтись, однако их состав можно «ослабить», заменив двух ферзей ладьями или даже ладьей с королем или слоном: