Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А.

Нажмите для полного просмотра!

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №2

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №3

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №4

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №5

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №6

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №7

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №8

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №9

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №10

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №11

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №12

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №13

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №14

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №15

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №16

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №17

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №18

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №19

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №20

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №21

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №22

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №23

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №24

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А., слайд №25

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А.. Доклад-сообщение содержит 25 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Задачи на построение с помощью одной линейки Выполнила: Иванченко И.А.

Слайд 2

Описание слайда:

О решении задач на построение Решение задач на построение состоит из 4 этапов: Анализ Построение Доказательство Исследование

Слайд 3

Описание слайда:

Теорема Дезарга Если прямые, соединяющие соответственные вершины двух треугольников, пересекаются в одной точке, то соответственные прямые, содержащие стороны треугольников пересекаются в трех точках, лежащих на одной прямой (см. рис.)

Слайд 4

Описание слайда:

Доказательство теоремы Дезарга Докажем теорему Дезарга с помощью теоремы Менелая. Теорема Менелая. Точки A1 , B1 и C1 , расположенные соответственно на прямых BC, CA, AB и не совпадающие с вершинами треугольника ABC, лежат на одной прямой тогда и только тогда, когда (см. рис.) AB1 CA1 BC1 * * = -1. B1C A1B C1A

Слайд 5

Описание слайда:

Для доказательства принадлежности точек U, V, W одной прямой, рассмотрим АВС и точки U, V, W , лежащие на прямых, содержащих стороны АВ, ВС, АС этого треугольника и докажем, что Для доказательства принадлежности точек U, V, W одной прямой, рассмотрим АВС и точки U, V, W , лежащие на прямых, содержащих стороны АВ, ВС, АС этого треугольника и докажем, что Для этого применим теорему Менелая для треугольников, SАВ, SBC, SAC и их секущих (A/B/), (В/С/), (А/С/) соответственно. Тогда для  SАВ и секущей (А/В/) имеем: Для  SВС и секущей (В/С/) имеем:

Слайд 6

Описание слайда:

Для  SАС и секущей (А/С) имеем: Для  SАС и секущей (А/С) имеем: Умножим на и поделим на Получаем: В итоге получили равенство

Слайд 7

Описание слайда:

Модификации теоремы Дезарга Теорема 1. Дано: ABC и A/B/C/ таковы, что AA/  BB/ CC/ = S, AB  A/B/ = U, BC  B/C/ = V, AC  A/C/ = W. Доказать: что W, V, U лежат на одной прямой.

Слайд 8

Описание слайда:

Теорема 2. Теорема 2. Дано: ABC и A/B/C/ AA/ // BB/ // CC/ , AB  A/B/ = X, BC  B/C/ = Y, AC  A/C/ = Z. Доказать: X, Y, Z лежат на одной прямой.

Слайд 9

Описание слайда:

Теорема 3. Дано: ABC и A/B/C/ AA/  BB/ CC/ = S, AB  A/B/ = X, BC  B/C/ = Y, AC // A/C/ Доказать: XY//AC

Слайд 10

Описание слайда:

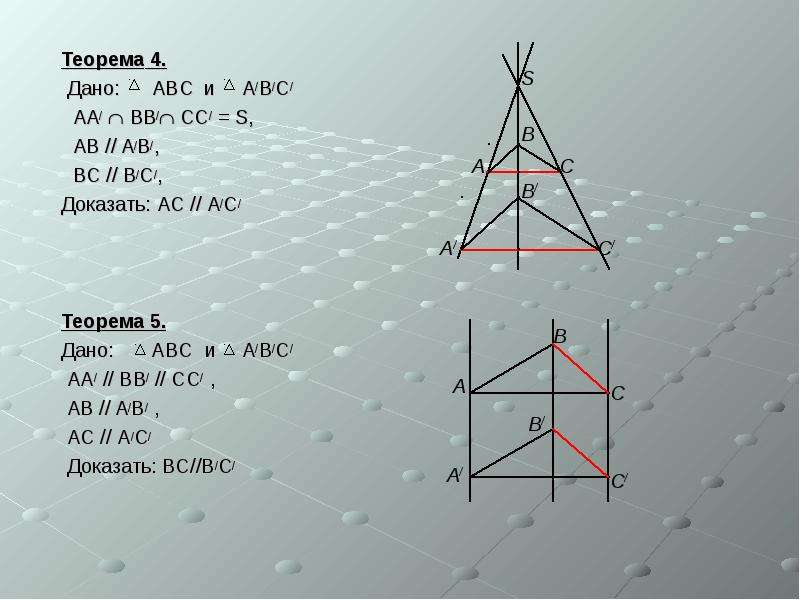
Теорема 4. Теорема 4. Дано: ABC и A/B/C/ AA/  BB/ CC/ = S, AB // A/B/, BC // B/C/, Доказать: AC // A/C/ Теорема 5. Дано: ABC и A/B/C/ AA/ // BB/ // CC/ , AB // A/B/ , AC // A/C/ Доказать: BC//B/C/

Слайд 11

Описание слайда:

Применение теоремы Дезарга для построения параллельных прямых (с помощью одной линейки) Задача. Даны две различные параллельные прямые а и b и точка А, не лежащая на них. Через точку А проведите прямую, параллельную данным прямым.

Слайд 12

Описание слайда:

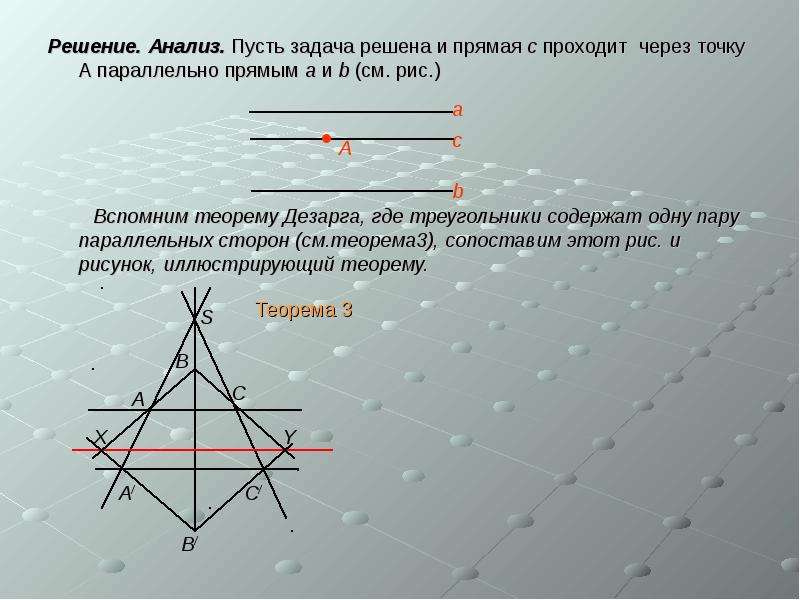
Решение. Анализ. Пусть задача решена и прямая с проходит через точку А параллельно прямым а и b (см. рис.) Решение. Анализ. Пусть задача решена и прямая с проходит через точку А параллельно прямым а и b (см. рис.) Вспомним теорему Дезарга, где треугольники содержат одну пару параллельных сторон (см.теорема3), сопоставим этот рис. и рисунок, иллюстрирующий теорему. Теорема 3

Слайд 13

Описание слайда:

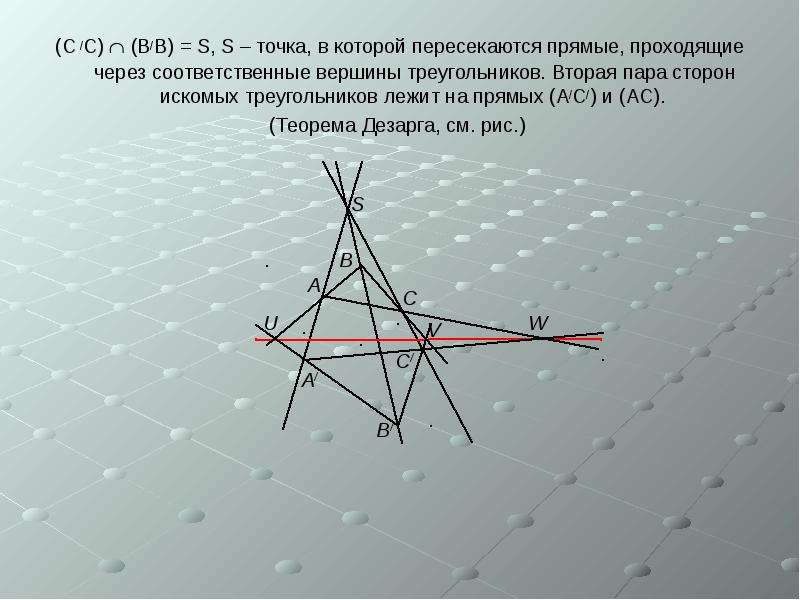
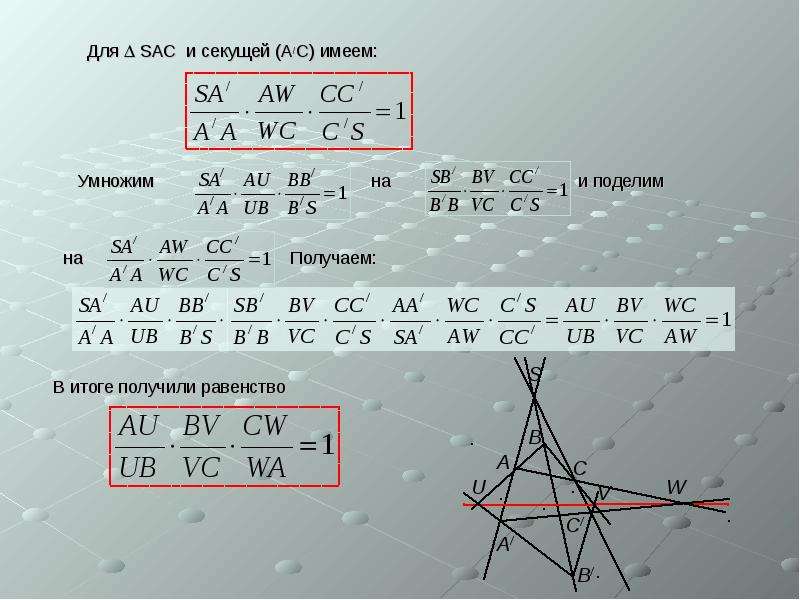
В этой задаче первоначальный рисунок В этой задаче первоначальный рисунок ничего не выражает. В нашем случае прямые а и в – это прямые, на которых лежат две соответственные стороны треугольников с осью с. Тогда точка А является точкой пересечения одной пары соответственных сторон. Ещё одна пара соответственных сторон должна пересекаться в точке, также лежащей на с. Построение, таким образом, сводится к построению двух треугольников, одна пара соответственных сторон которых лежит на прямых а и в. Поэтому на прямых а и в возьмем произвольные отрезки: [С1В1]  а, [СВ]  в в качестве соответственных сторон, а вторая пара сторон пересекается в точке А.

Слайд 14

Описание слайда:

(С /С)  (В/В) = S, S – точка, в которой пересекаются прямые, проходящие через соответственные вершины треугольников. Вторая пара сторон искомых треугольников лежит на прямых (А/С/) и (АС). (С /С)  (В/В) = S, S – точка, в которой пересекаются прямые, проходящие через соответственные вершины треугольников. Вторая пара сторон искомых треугольников лежит на прямых (А/С/) и (АС). (Теорема Дезарга, см. рис.)

Слайд 15

Описание слайда:

Построение: Построение: Берем точки С1, В1  а Берем точки С, В,  в S = (СС1)  (ВВ1) Проведем произвольную прямую l  S О1 = l  (С1А) О = l  (СА) 6. (В1О1)  (ВО) = А1 (АА1) = с – искомая l Доказательство: Рассмотрим С1О1В1 и  СОВ. (СС1)  (ВВ1)  (ОО1) = S по построению. Точки А = (С1О1)  (СО) и А1 = (В1О1)  (ВО) определяют прямую с. Поскольку (С1В1) // (СВ), то с // а // в.

Слайд 16

Описание слайда:

Исследование: Задача всегда имеет единственное решение, так как через данную точку можно провести единственную прямую, параллельную данной.

Слайд 17

Описание слайда:

Задача с недоступными элементами Точку называют недоступной, если к ней нельзя применить аксиомы конструктивной геометрии, в частности, аксиома линейки и циркуля. Фигура считается недоступной, если все ее точки недоступны. Недоступная точка считается заданной (известной), если построены отрезки двух прямых, пересекающихся в этой точке.

Слайд 18

Описание слайда:

Слайд 19

Описание слайда:

Так как точки М и L лежат на одной прямой, то можно рассмотреть их как точки пересечения соответственных сторон треугольников, а прямые а и в взять как прямые ВС и В'С', то есть прямые, на которых лежат две соответственные стороны треугольников с осью с. Таким образом, построение сводится к построению двух треугольников, две стороны которых лежат на сторонах а и в, а другая пара соответственных сторон пересекаются в точке М. Необходимо построение проводить таким образом, чтобы прямые пересекались в доступной части чертежа. Так как точки М и L лежат на одной прямой, то можно рассмотреть их как точки пересечения соответственных сторон треугольников, а прямые а и в взять как прямые ВС и В'С', то есть прямые, на которых лежат две соответственные стороны треугольников с осью с. Таким образом, построение сводится к построению двух треугольников, две стороны которых лежат на сторонах а и в, а другая пара соответственных сторон пересекаются в точке М. Необходимо построение проводить таким образом, чтобы прямые пересекались в доступной части чертежа.

Слайд 20

Описание слайда:

Построение: Построение: 1. Возьмем точки А, В  а; А/, В/  b (см. рис.) 2. Точка S = (АА/)  (ВВ/). 3. Проведем произвольную прямую l: S  l. 4. С1 = (В/М)  l, С = (ВМ)  l. 5. (АС)  (А/С/) = М1 (ММ1) = с – искомая. Доказательство: Рассмотрим  АВС и  А/В/С/. В них: (ВВ/)  (АА/)  (СС/) = S (АС)  (А/С/) = М1, (ВС)  (В/С/) = М, (АВ)  (А/В/) = а  в = L, следовательно, по теореме 1 точки М, М1 и L лежат на одной прямой.

Слайд 21

Описание слайда:

Поляра Четыре точки A, B, C, D, лежащие на одной прямой, образуют гармоническую четверку, если AC AD : = -1. CB DB Задача. Из данной точки A проведены к данной окружности с центром O касательные AK1 , AK2 и секущая, пересекающая окружность в точках C и D, а отрезок K1K2 – в точке B. Докажите, что точки A, B, C и D образуют гармоническую четверку.

Слайд 22

Описание слайда:

Доказательство: Введем систему координат с началом в точке A, как показано на рисунке. Доказательство: Введем систему координат с началом в точке A, как показано на рисунке. Пусть B1, C1, D1 – проекции точек B, C, D на ось абсцисс. Докажем, что точки A, B1, C1, D1 образуют гармоническую четверку. Отсюда сразу же последует, что точки A, B, C, D также образуют гармоническую четверку. Уравнение окружности запишем в виде (x – a)2 + y2 = R2 (2) где a = AO, R – радиус окружности, а уравнение секущей AD – в виде y = kx (3) где k – некоторое число. Координаты точек C и D удовлетворяют уравнениями (2) и (3). Если подставить y = kx в уравнение (2), то придем к квадратному уравнению (1 + k2) x2 – 2ax + a2 – R2 = 0 (4)

Слайд 23

Описание слайда:

корни x1 и x2 которого равны абсциссам точек C и D, т.е. корни x1 и x2 которого равны абсциссам точек C и D, т.е. AC1 = x1, AD1 = x2. По теореме Виета 2a a2 – R2 x1 + x2 = , x1x2 = , 1+ k2 1 + k2 2x1x2 a2 – R2 откуда = (5) x1+ x2 a Рассматривая прямоугольный треугольник AOK1 , нетрудно a2 – R2 установить, что AB1 = . Поэтому если положить AB1= x0 , a то равенство (5) можно записать в виде 2x1x2 = x0, или x1(x2 – x0) – x2(x0 – x1) =0. x1+x2

Слайд 24

Описание слайда:

Отсюда, учитывая, что Отсюда, учитывая, что x1(x2 – x0) = AC1 * B1D1 , x2(x0 – x1) = AD1 * C1B1 , получаем: AC1 * B1D1 – AD1* C1B1 =0, а это и означает, что точки A, B1 , C1 , D1 образуют гармоническую четверку. 2x1x2 Замечание. Равенство = x0 можно доказать и не прибегая x1 + x2 к рассмотрению треугольника AOK1. В самом деле, соотношение 2x1x2 a2 – R2 2x1x2 = показывает, что величина не зависит от x1+ x2 a x1 + x2 k, т.е.имеет одно и то же значение для любой прямой, описываемой уравнением y = kx. Возьмем k таким, чтобы уравнение y = kx было уравнением касательной AK1. Тогда оба корня x1 и x2 квадратного уравнения (1 + k2) x2 – 2ax + a2 – R2 = 0 будут равны абсциссе точки K1 , т.е. будут равны x0.

Слайд 25

Описание слайда:

Но в этом случае Но в этом случае 2x1x2 2x0x0 = = x0 , x1 + x2 x0+x0 2x1x2 а значит, и для любой другой прямой = x0 x1 + x2 Прямая K1K2 называется полярой данной точки A относительно данной окружности. Если точка B не лежит на поляре, а прямая AB пересекает окружность в точках C и D, то можно сделать такой вывод: если данная точка A лежит вне данной окружности, то множество точек B, для каждой из которых точки пересечения прямой AB и окружности гармонически разделяют точки A и B, представляет собой часть поляры точки A относительно данной окружности, лежащую внутри этой окружности.