Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе

Нажмите для полного просмотра!

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №2

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №3

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №4

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №5

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №6

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №7

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №8

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №9

Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе, слайд №10

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Скачать презентацию Алгоритмы на графах: определение наличия циклов в графе. Доклад-сообщение содержит 10 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Слайд 2

Описание слайда:

Домашнее задание Какое максимальное количество рёбер может быть в ориентированном ациклическом графе с n вершинами? Может ли быть так, что правильным результатом топологической сортировки графа оказывается любой порядок его вершин? Решить задачу о производстве деталей с помощью DFS. Как использовать топологическую сортировку для определения наличия циклов в графе?

Слайд 3

Описание слайда:

Циклы и топологическая сортировка

Слайд 4

Описание слайда:

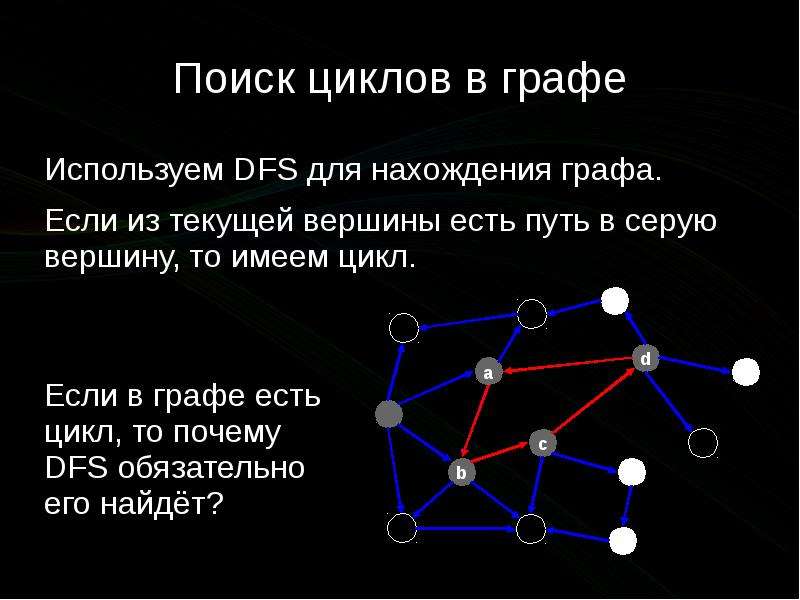
Поиск циклов в графе

Слайд 5

Описание слайда:

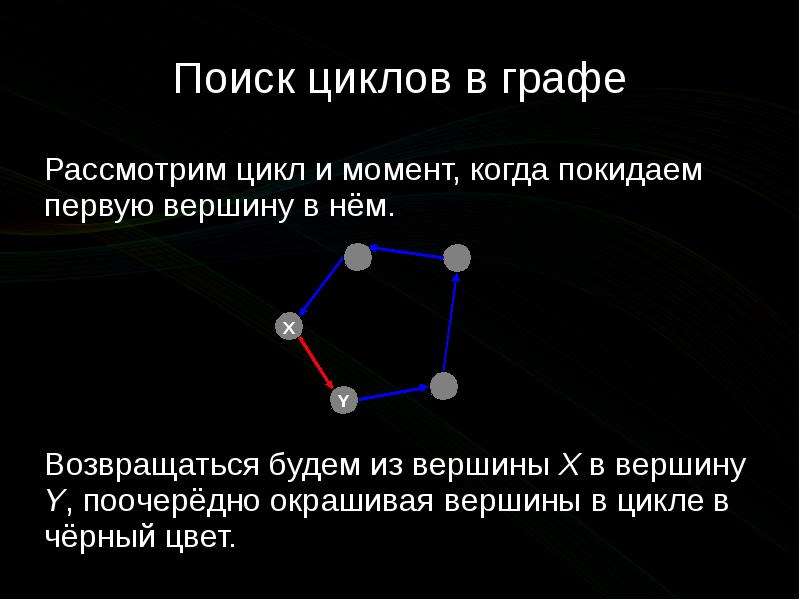
Поиск циклов в графе

Слайд 6

Описание слайда:

Поиск циклов в графе

Слайд 7

Описание слайда:

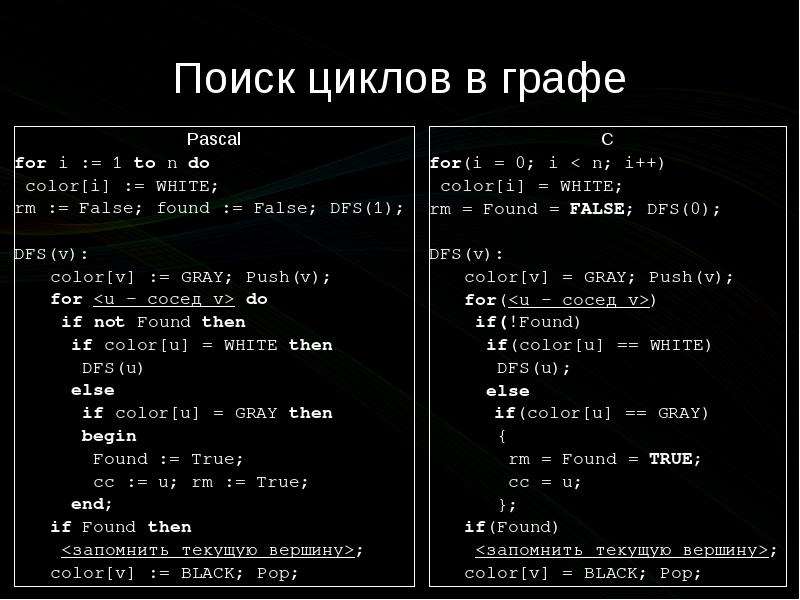
Поиск циклов в графе

Слайд 8

Описание слайда:

Поиск циклов в графе

Слайд 9

Описание слайда:

Поиск циклов в графе В первой строке файла input.txt заданы целые n и m — соответственно число вершин и число рёбер ориентированного графа (1 ≤ n ≤ 10 000, 0 ≤ m ≤ 50 000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами. В файл output.txt вывести последовательность номеров вершин, соответствующих любому циклу в графе. Если граф ациклический, то вывести 0. Ограничение по времени — 1 сек. Ограничение по памяти — 16 Мб.

Слайд 10

Описание слайда:

Домашнее задание Верно ли утверждение, что из всех циклов в графе, проходящих через начальную вершину, DFS прежде всего находит цикл минимальной длины? Привести доказательство или контрпример. Решить задачу об определении наличия циклов в ориентированном графе проверкой рёбер: в выходной файл вывести 1, если в графе есть циклы, и 0 в противном случае. Выполнить п. 2 для неориентированного графа. Решить задачу об отыскании цикла в ориентированном графе с помощью DFS без использования второго стека.