Описание слайда:
конспект
Конспект открытого урока по геометрии в 11-ом классе по теме «Объем конуса»
Цель урока:
Образовательные – познакомить учащихся с формулой объема конуса; организовать деятельность учащихся по выработке умений и навыков решения задач по вычислению объема конуса (в том числе практико-ориентированных задач), обеспечить повторение и систематизацию материала темы. Создать условия для контроля усвоения знаний и умений. Способствовать выработке умения использовать ИКТ.
Развивающие - развивать активность, мышление, умение анализировать, использовать рациональные приемы работы.
Воспитательные – способствовать воспитанию ответственного отношения к обучению и в частности к изучению математики.
Тип урока: изучение нового материала.
План урока.
1. Орг. момент
2. Постановка темы и цели урока
3. Контроль над выполнением домашнего задания
4. Актуализация знаний
5. Изучение нового материала
6. Закрепление: решение практико-ориентированной задачи на конус безопасности, решение задач из открытого банка задач, решение задач из учебника
7. Задание на дом.
Ход урока.
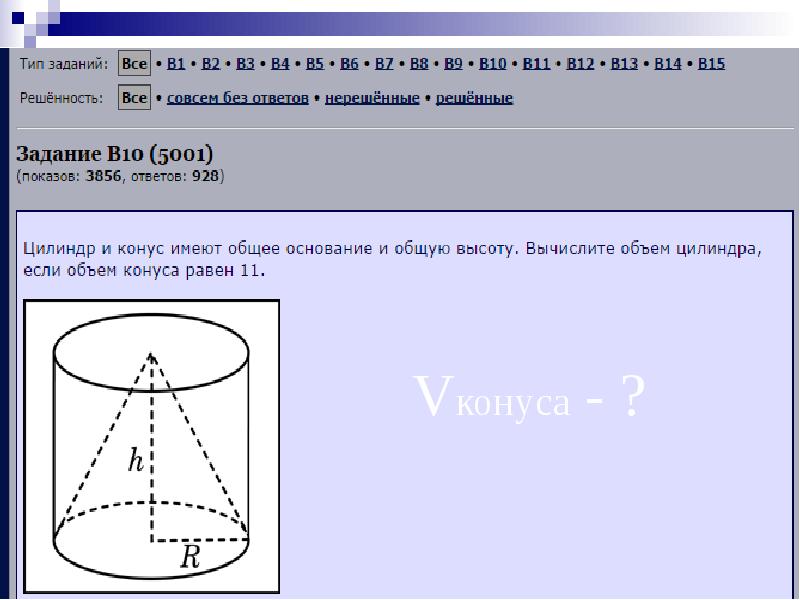
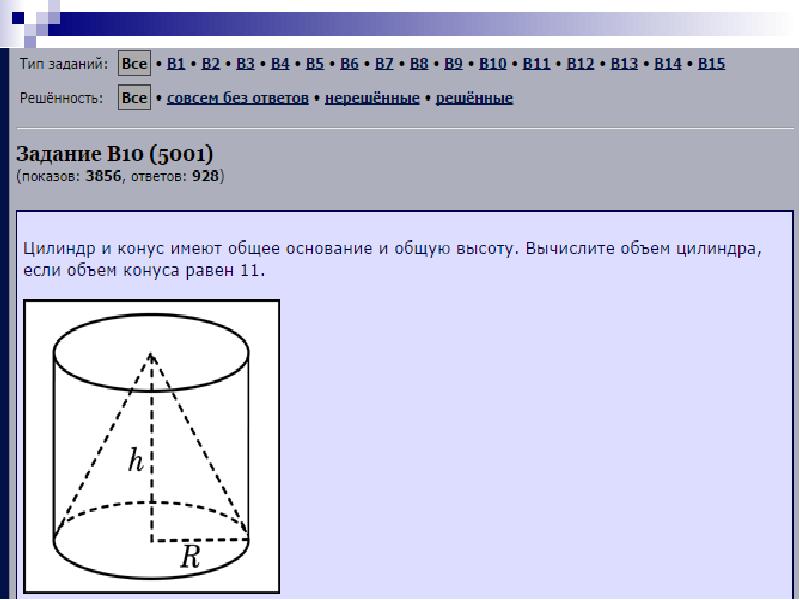
Как вы помните, последние несколько уроков мы изучаем объемы тел. И на прошлом уроке мы приступили к изучению объемов тел вращения. Напомните, какие тела вращения изучаются в курсе геометрии 11-го класса? <Цилиндр, конус, шар>. (слайд) Верно. Объем какого тела вращения мы изучили на прошлом уроке?<Объем цилиндра>. (слайд) Верно. И на прошлом уроке, при решении задач из открытого банка ЕГЭ, нам встретилась задача на нахождение объема цилиндра, которую мы не смогли решить. Вот эта задача. (слайд) <на экране Задание B10 (5001)Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 11.
Ответ: 33 >
Кто помнит, почему мы не смогли решить эту задачу? <Чтобы ее решить, надо уметь находить объем конуса>. (слайд) Верно, и тогда мы решили, что на следующем уроке, т.е. сегодня, нам надо научиться…? <находить объем конуса>
Верно, сегодня мы учимся находить объем конуса. (слайд) Откройте тетради, запишите число и тему урока «Объем конуса». Итак, сегодня нам предстоит вывести формулу объема конуса.
Но сначала (слайд) проверим выполнение вами домашнего задания. На дом вам были заданы две задачи: одна из открытого банка задач, вторая - №5 учебника. В первой задаче (слайд) (Задание B10 (4963)
В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Ответ: 8.5)
вас просили найти объем цилиндра. План решения мы на прошлом уроке разобрали. У кого-нибудь возникли трудности при решении задачи?<Нет>. Какие ответы получили? <Прохожу по рядам, смотрю решение>.(слайд) Прекрасно, у всех правильный ответ. Посмотрим, как справились с задачей №5 учебника. Чья очередь была составить презентацию на решение домашней задачи из учебника? <Н.Н.> Справилась? <Да>. Прошу продемонстрировать у доски. <Ученица выходит с флэшкой и комментирует решение по своей презентации>. Прекрасно, решение задачи верное, работа оформлена грамотно и за эту работу Н.Н. получает оценку «5». У остальных такой же ответ? <Да>. (слайд)
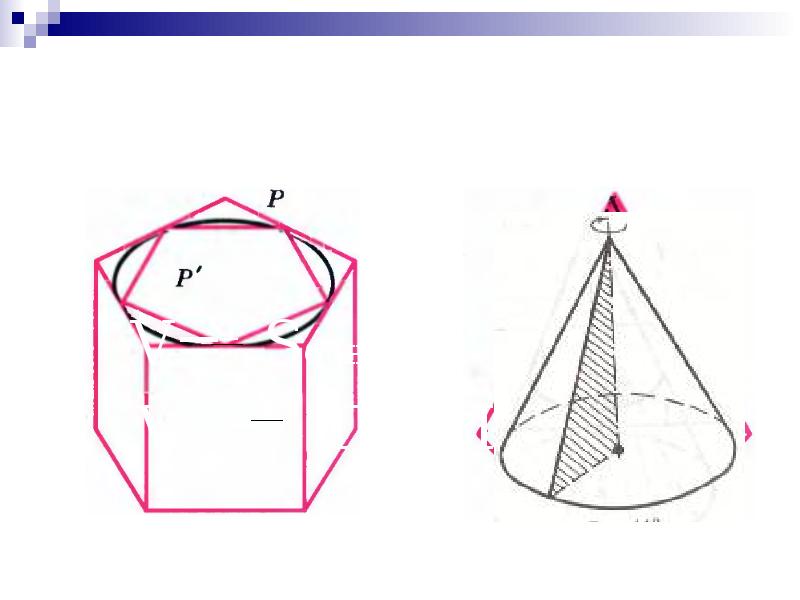
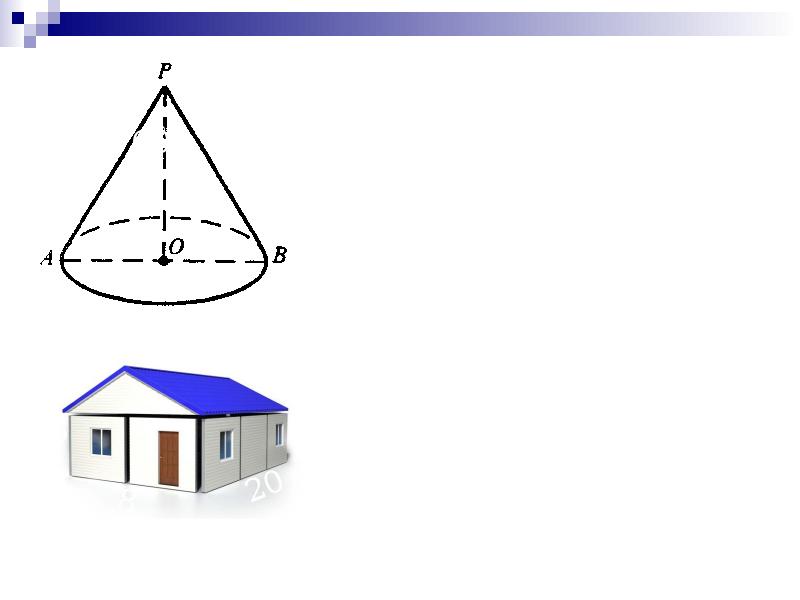
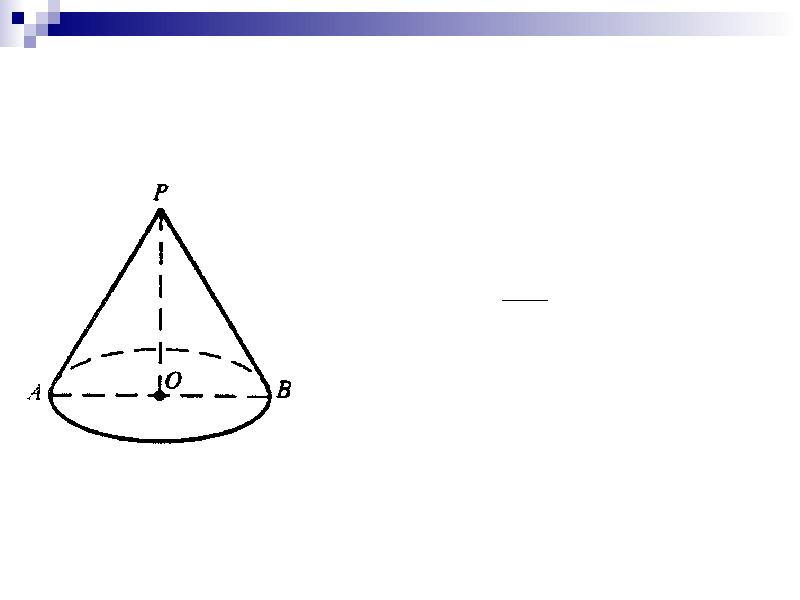
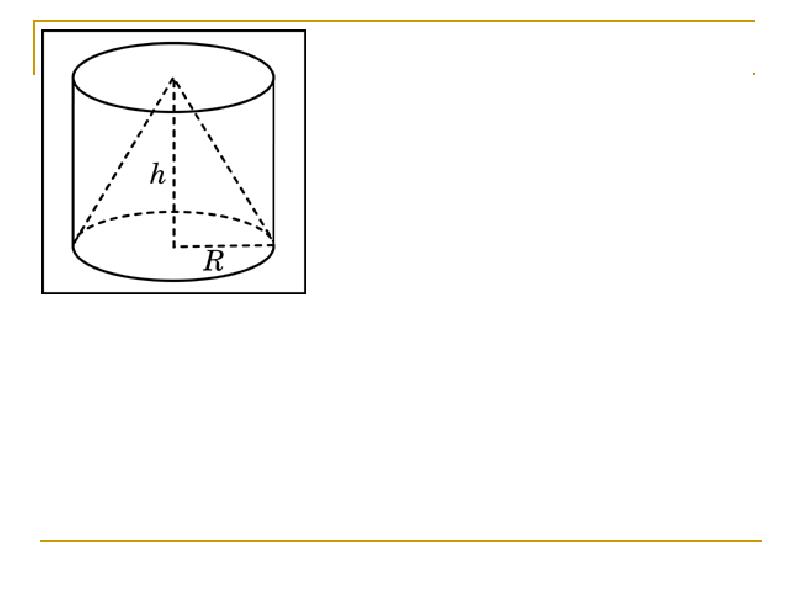
Ну что же, давайте приступим к изучению новой темы «Объем конуса». Начнем с определений конуса как геометрического тела и как тела вращения.< На доске изображение конуса. Учащиеся формулируют 2 определения конуса>. Верно. Практически на каждом уроке я говорю вам о принципе аналогии в геометрии, вот и формулу объема конуса мы получим аналогично тому, как получили ее для объема цилиндра. (слайд) Поэтому, давайте вспомним, как мы получили формулу объема цилинра? <Формулу объема цилиндра мы получили из формулы объема призмы>. (слайд) Так как же найти объем цилиндра? <Объем цилиндра равен произведению площади основания на высоту>. (слайд) Т.е. так же как и объем какого тела? <Призмы>. Верно, а призма, как мы помним, и является аналогом цилиндра среди многогранников. А какой многогранник является аналогом среди многогранников для конуса? <Пирамида>.(слайд) Значит формулу объема конуса мы можем получить из …? <из формулы объема пирамиды>. Верно, а как найти объем пирамиды? <Объем пирамиды равен 1/3 произведения площади основания на высоту>. (слайд) Тогда попробуем предположить, чему равен объем конуса, если объем цилиндра находится также, как объем призмы? <Объем конуса находится также, как объем пирамиды, т.е. объем конуса равен 1/3 произведения площади основания на высоту>. Хорошее предположение. (слайд) Давайте проверим так ли это, действительно ли объем конуса равен 1/3 произведения площади основания на высоту? При выведении формулы объема цилиндра (слайд) мы около цилиндра описали и вписали в него призмы. Значит около конуса надо …? <описать и вписать пирамиду>. (слайд) Так же как с цилиндром, при неограниченном увеличении числа сторон многоугольников в основаниях пирамид, площади многоугольников неограниченно приближается к …? <площади круга в основании конуса>. Тогда объем этих пирамид неограниченно приближается к 1/3 площади основания конуса на высоту конуса. А мы знаем, что данное тело имеет объем V, если существуют содержащие его простые тела и содержащиеся в нем простые тела с объемами сколь угодно мало отличающимися от V. Значит, действительно, (слайд) объем конуса равен 1/3 произведения площади основания на высоту. . Видим, что наше предположение оправдалось, т.е. объем конуса равен 1/3 произведения площади основания на высоту. А, зная, что площадь основания конуса равна…? <ПR2>, то формулу объема конуса можно представить(слайд) в виде V=1/3ПR2H. (слайд) Постройте изображение конуса в тетради и запишите формулу объема конуса. К слову сказать, существует множество других способов вывода формулы объема конуса. Поэтому желающие получить «пятерку» по геометрии к следующему уроку могут подготовить доклад о различных способах вывода формулы объема конуса. Информации по данному вопросу в Интернете достаточно.
Теперь, зная как найти объем конуса, можно вернуться к задаче(слайд) Задание B10 (5001)Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 11.
Ответ: 33 >
Давайте посмотрим, какие задачи на объем конуса представлены в банке задач ЕГЭ. (слайд)
Задание B10 (5021)Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 2
Отлично, идем дальше. Еще при изучении темы «Конус» мы выяснили, что многие окружающие нас тела и предметы или части предметов имеют форму конуса. (слайд) Это горы, (слайд) воронка, луч кинопроектора, детали механизмов, шестерни, (слайд) носовая часть самолетов и ракет, (слайд) пожарное ведро. А знает ли кто-нибудь, почему пожарное ведро имеет форму конуса? (слайд) <Информация>
Продолжим. (слайд) В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
В(слайд) биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
«Конусами» (слайд) называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи.
В(слайд) физике встречается понятие «телесный угол». Это конусообразный угол, вырезанный в шаре. А еще есть такое понятие, как конус безопасности. Кто-нибудь знает, что такое конус безопасности? <Нет>.(слайд) Так вот, по статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 000 000 жителей (чаще в южных странах). Поэтому в районах повышенной опасности поражением молнией устанавливают…? <Громоотводы>. Громоотвод и образует конус безопасности.
Рядом с нашей школой тоже установлен громоотвод.
Давайте(слайд) узнаем, будет ли защищена во время грозы наша школа высотой 5 м, шириной 8 м и длиной 20 м, если высота громоотвода 7 м, а угол между громоотводом и образующей конуса безопасности равен 60? Для удобства вычислений будем считать, что наша школа имеет форму прямоугольного параллелепипеда.
60Решение задачи: Найдем объемы конуса и школы.
По определению тангенса ,
7
,
R
Vк = (1/3) 3,14 122 7 = 1055 м3
Объем школы: 5х8х20=800
Vк > Vш => школа будет защищена от молнии.
Ответ: школа будет защищеа от грозы.
Прекрасно, а теперь посмотрим какие задачи на тему «Объем конуса» нам предлагает учебник. Давайте рассмотрим задачу №7 на странице 128. «Куча щебня имеет коническую форму, радиус основания которой 2 м, а образующая 2,5 м. Найти объем кучи щебня».<ответ: 6,28 м3> .
И так, ребята, урок наш идеек к концу, поэтому давайте вспомним что мы сегодня узнали, чему научились? (слайд) <Мы научились находить объем конуса>. Так как же найти объем конуса? <Объем конуса равен 1/3 произведения площади основания на высоту>. (слайд) Верно.
А сейчас откройте дневники (слайд) и запишите задание на дом: п 74, напоминаю, желающие могут подготовить доклад о различных способах вывода формулы объема конуса, и 2 задачи: первая задача из банка (слайд) (Задание B10 (4997) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.), <Раздать карточки с ДЗ. Если позволяет время разобрать задачи>, и сегодня очередь О.К. готовить презентацию на решение домашней задачи. Условие второй задачи прочитает Б.А. <Найти объем пожарного ведра, если диаметр основания 50 см, а образующая 40см. Ответ указать в литрах>. Напоминаю, (слайд) что один литр – это 1 кубический дециметр. А на следующем уроке мы с вами попробуем вычислить объем обычного ведра. (слайд) Как вы считаете, что нам для этого потребуется, объем какого тела (слайд)для этого надо уметь находить. <Объем усеченного конуса>. Верно, значит, на следующем уроке мы будем изучать объем усеченного конуса. Спасибо за урок, все свободны.