Основные свойства функции - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Основные свойства функции. Доклад-сообщение содержит 17 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

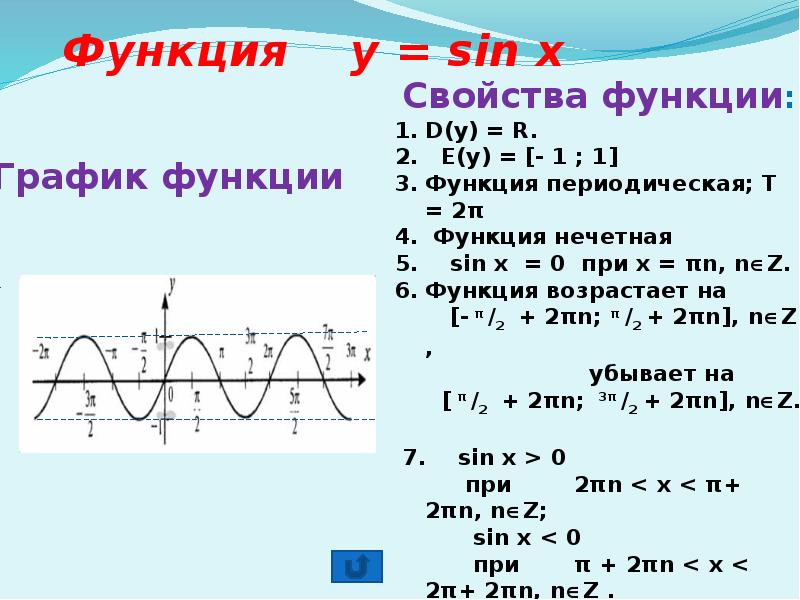
Содержание 1. Основные свойства функции. 2. Функция y = sin x. 2.1. Свойства и график. 2.2. График функции y = sin (x ± b). 2.3. График функции y = sin x ± b. 3. Функция y = cos x. 3.1. Свойства и график. 3.2. График функции y = cos (x ± b). 3.3. График функции y = cos x ± b. 4. Функция y = tg x: свойства и график 5. Функция y = ctg x: свойства и график.

Слайд 2

Описание слайда:

Основные свойства функции. 1. Область определения. 2. Область значений. 3. Периодичность. 4. Четность, нечетность. 5. Нули. 6. Промежутки монотонности. 7. Промежутки знакопостоянства. 8. Наибольшее и наименьшее значения.

Слайд 3

Описание слайда:

Функция y = sin x

Слайд 4

Описание слайда:

Слайд 5

Описание слайда:

Слайд 6

Описание слайда:

Функция y = cosx

Слайд 7

Описание слайда:

Слайд 8

Описание слайда:

Слайд 9

Описание слайда:

Функция y = tg x

Слайд 10

Описание слайда:

Функция y = ctg x

Слайд 11

Описание слайда:

Исследование тригонометрических функций на четность y = sin x. Функция нечетная. 1) (-x)  D(y). 2) y(-x) = sin (-x) = - sin x = - y(x). y = cos x . Функция четная. 1) (-x)  D(y). 2) y(-x) = cos (-x) = cos x = y(x). y= tg x. Функция нечетная. 1) (-x)  D(y). 2) y(-x) = tg (-x) = - tg x = - y(x). y= ctg x. Функция нечетная. 1) (-x)  D(y). 2) y(-x) = ctg (-x) = - ctg x = - y(x).

Слайд 12

Описание слайда:

Периодичность тригонометрических функций. y = sin x. Период Т = 2 π. (y = cos x. Т = 2 π) Доказательство. 1) (x ± 2 π)  D(y). 2) y(x + 2 π) = sin (x + 2 π) = sin x = y (x). 3) y(x - 2 π) = sin (x - 2 π) = sin x = y (x). 4) y(x ± 2 π) = y (x). Следовательно, Т = 2π. (Для функции y = cos x доказательство аналогично)

Слайд 13

Описание слайда:

Периодичность тригонометрических функций.

Слайд 14

Описание слайда:

Монотонность тригонометрических функций. y = cos. Функция возрастает на [ π+ 2πn; 2π+ 2πn], nZ, убывает на [ 2πn; π+ 2πn], nZ. Доказательство. 1) При повороте точки (1; 0) вокруг начала координат против часовой стрелки на угол от 0 до π π (1; 0) 0 абсцисса точки, т.е cos x, -1 1 уменьшается от 1 до -1. Поэтому если 0 ≤ Х1 < Х2 ≤ π то cos Х1> cos Х2. Это означает, что функция y = cos x убывает на [ 0; π]. 2) Функция y = cos x возрастает на [ -π; 0], т.к. она убывает на [0; π] и является четной. 3) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [ π+ 2πn; 2π+ 2πn], nZ, убывает на [ 2πn; π+ 2πn], nZ.

Слайд 15

Описание слайда:

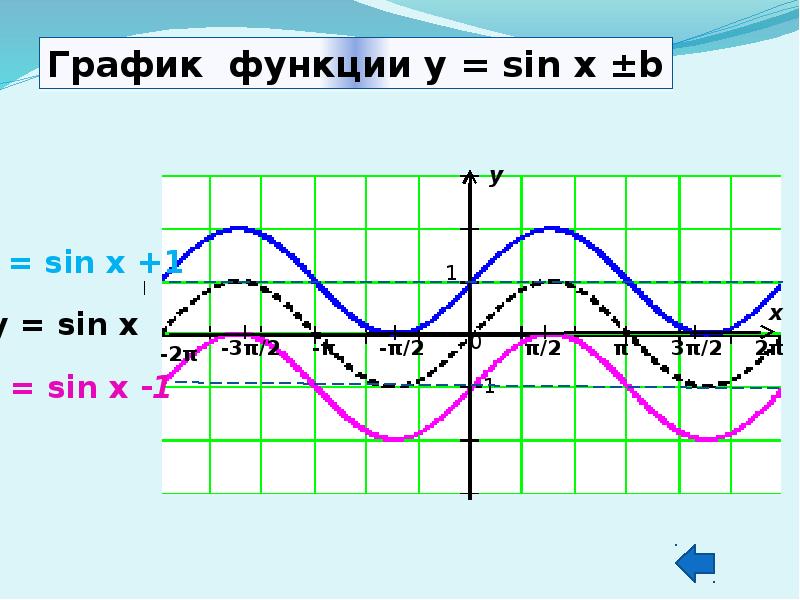
Монотонность тригонометрических функций. y = sin x. Функция возрастает на [- π /2 + 2πn; π /2 + 2πn], nZ , убывает на [ π /2 + 2πn; 3π /2 + 2πn], nZ. Доказательство. 1) При повороте 1 π /2 точки вокруг начала координат против часовой стрелки на угол от - π /2 до π /2 ордината точки, т.е sin x, увеличивается от -1 до 1. Поэтому если - π /2 ≤ Х1 < Х2 ≤ π /2 , то sin Х1< sin Х2. -1 - π /2 Это означает, что функция y = sin x возрастает на [- π /2 ; π /2 ]. 2) Т.к. функция периодическая с периодом Т = 2π, то она возрастает на [- π /2 + 2πn; π /2 + 2πn], nZ . Убывание функции на [ π /2 + 2πn; 3π /2 + 2πn], nZ, доказывается аналогично.

Слайд 16

Описание слайда:

Определение промежутков знакопостоянства тригонометрических функций. y = tg x tg x > 0 при πn < x < π /2 + πn, nZ; — + tg x < 0 при - π /2 + πn < x < πn, nZ . + — y = ctg x ctg x > 0 при πn < x < π /2 + πn, nZ; ctg x < 0 при π /2 + πn < x < π + πn, nZ.

Слайд 17

Описание слайда:

Определение промежутков знакопостоянства тригонометрических функций. y = sin x . + + sin x > 0 при 2πn < x < π+ 2πn, nZ; sin x < 0 при π + 2πn < x < 2π+ 2πn, nZ . _ _ y = cos x. cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, nZ; _ + cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, nZ. − +