Элементы математической статистики - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Элементы математической статистики, слайд №1

Элементы математической статистики, слайд №2

Элементы математической статистики, слайд №3

Элементы математической статистики, слайд №4

Элементы математической статистики, слайд №5

Элементы математической статистики, слайд №6

Элементы математической статистики, слайд №7

Элементы математической статистики, слайд №8

Элементы математической статистики, слайд №9

Элементы математической статистики, слайд №10

Элементы математической статистики, слайд №11

Элементы математической статистики, слайд №12

Элементы математической статистики, слайд №13

Элементы математической статистики, слайд №14

Элементы математической статистики, слайд №15

Элементы математической статистики, слайд №16

Элементы математической статистики, слайд №17

Элементы математической статистики, слайд №18

Элементы математической статистики, слайд №19

Элементы математической статистики, слайд №20

Элементы математической статистики, слайд №21

Элементы математической статистики, слайд №22

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Элементы математической статистики. Доклад-сообщение содержит 22 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Элементы математической статистики Введение. Задачи мат. статистики. Генеральная совокупность. Мат. статистика – это дисциплина, изучающая методы, которые по наблюдениям случайных величин позволяют сделать обоснованные выводы о распределении случайных величин и их характеристиках.

Слайд 2

Описание слайда:

§1. Понятия случайной выборки, вариационного ряда и статистики Пусть – с.в. с функцией распределения Определение 1. Набор независимых случайных величин , ,…, , каждая из которых имеет распределение , называется случайной выборкой объема , отвечающей случайной величине с функцией распределения В результате наблюдений с.в. , ,…, получены их конкретные числовые значения: , ,…, . Этот набор чисел , ,…, называют реализацией (значениями) случайной выборки , ,…, а числа - выборочными значениями. Итак, в мат. стат-ке с.в. (генеральная совокупность) исследуется на основании случайной выборки , ,…, , реализация которой есть , ,…, . Определение 2. Случайная величина, являющаяся функцией случайной выборки, называется статистикой. Например, с.в. - статистика.

Слайд 3

Описание слайда:

§2. Эмпирическая (выборочная)функция распределения

Слайд 4

Описание слайда:

Слайд 5

Описание слайда:

. .

Слайд 6

Описание слайда:

. График эмпирической функции распределения

Слайд 7

Описание слайда:

§3. Эмпирическая плотность распределения. Гистограмма Постановка задачи. Построение эмпирической плотности. По наблюдениям , ,…, определить промежуток в котором лежат все выборочные значения Разбить на k непересекающихся интервалов длины h. =[, ), j=1,2,…,k; =a; c) Для каждого подсчитать : - количество выборочных значений попавших в этот интервал. - частота наблюдений, попавших в . - относительная частота наблюдений, попавших в . =1.

Слайд 8

Описание слайда:

. Рассмотрим кусочно-постоянную функцию (), принимающую значения на ()- эмпирическая плотность распределения. 3. График эмпирической плотности () называют гистограммой. Для построения гистограммы следует на оси абсцисс отложить интервалы и каждому интервалу сопоставить число . Площадь всей полученной геометрической фигуры равна 1.

Слайд 9

Описание слайда:

Слайд 10

Описание слайда:

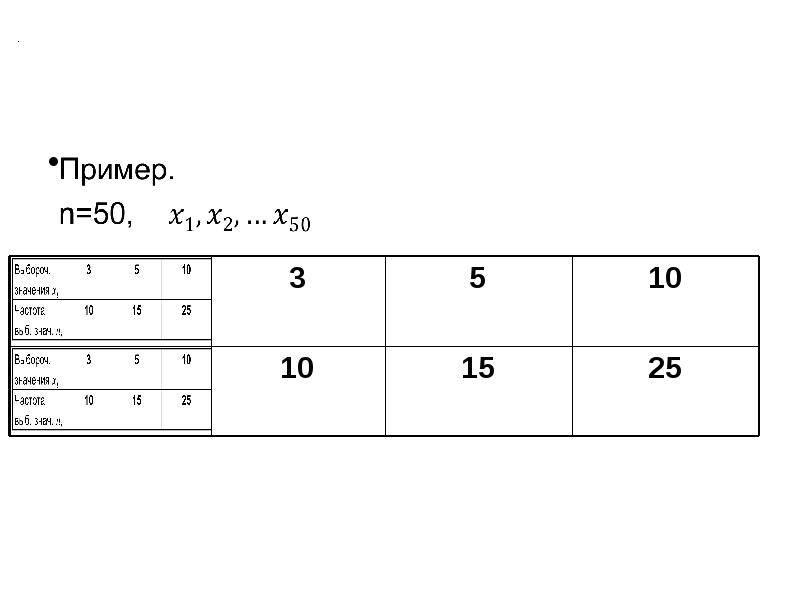
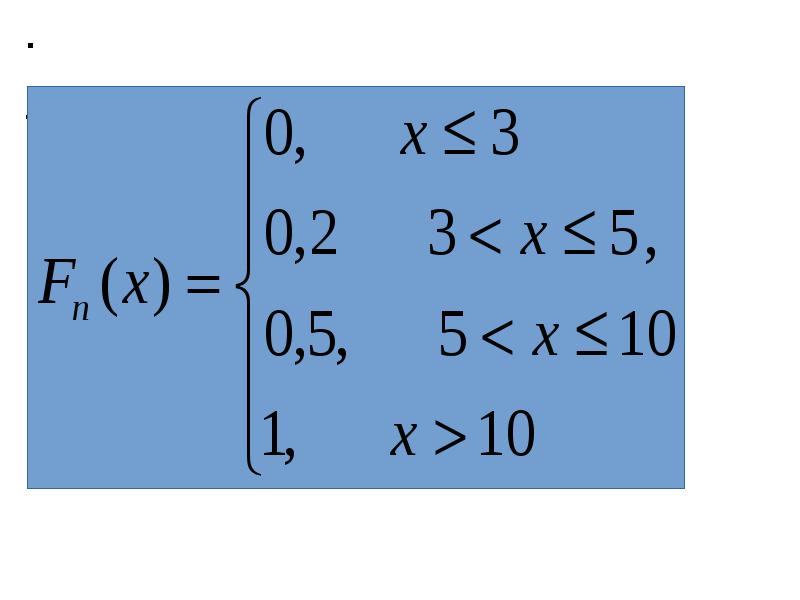
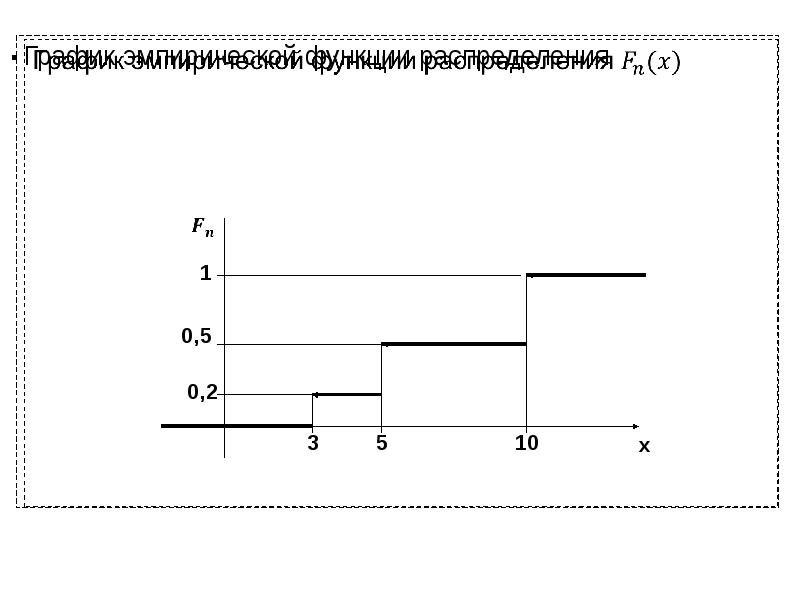
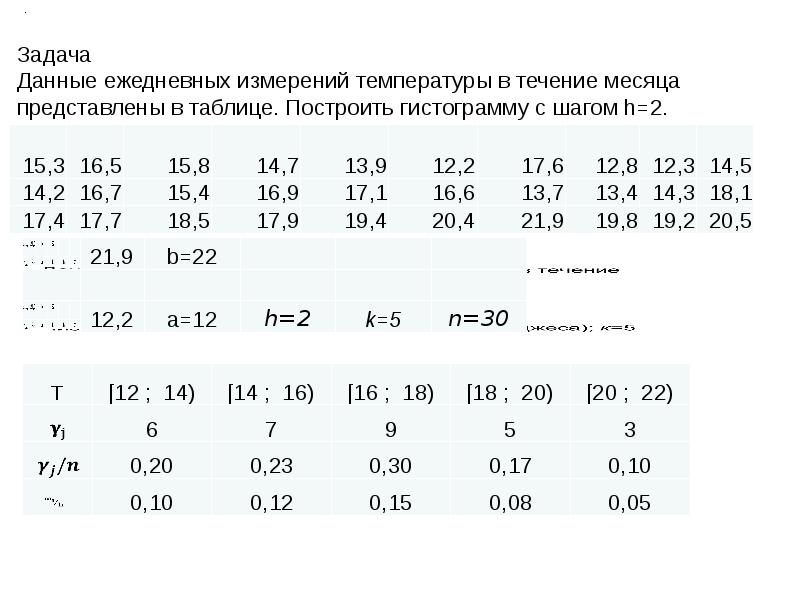
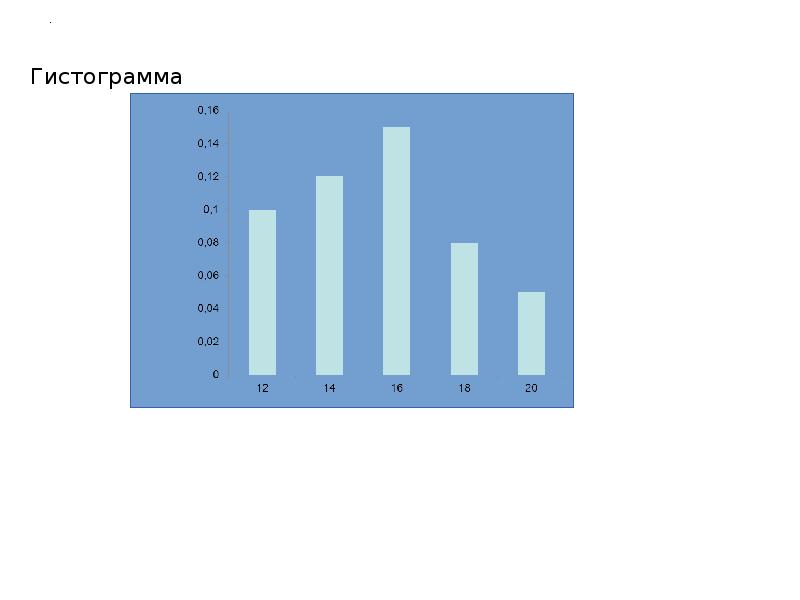
. Гистограмма

Слайд 11

Описание слайда:

. Соответствие между интервалами и частотами (относительными частотами ) называют группированным статистическим рядом. Группированный статистический ряд можно графически изобразить в виде гистограммы частот (относительных частот) , т.е. графика кусочно-постоянной функции со значениями () на интервале

Слайд 12

Описание слайда:

. При построении гистограмм мы имеем свободу в выборе промежутка [a,b] , числа интервалов разбиения k. Для получения хороших приближений для плотности неизвестного распределения следует всякий раз учитывать специфику конкретных данных. Самые общие рекомендации по выбору этих параметров таковы. Значение k должно быть существенно меньше, чем объем выборки n, но вместе с тем не слишком малым, чтобы гистограмма не теряла индивидуальные черты. Интервалы разбиения следует выбирать так, чтобы каждый из них содержал "достаточно много'' элементов выборки. Если в группах недостаточно большое число данных, то возможные случайные флуктуации их числа приводят к значительным искажениям реальной картины.

Слайд 13

Описание слайда:

. .

Слайд 14

Описание слайда:

§4. Оценивание параметров распределения Пусть некоторый параметр, характеризующий распределение с.в. . Пусть , ,…, - случайная выборка, отвечающая с.в. . (1) Построим с.в. =(, ,…, ). Функцию от случайной выборки, приближенно равную неизвестному параметру , называют оценкой . Оценка - это статистика, которая в определенном смысле близка к истинному значению параметра . Предположим, и неизвестны. Построим для этих параметров оценки. Выборочное среднее Опр. Выборочным средним, построенным по случайной выборке (1), называется с.в.

Слайд 15

Описание слайда:

2. Вычисление выборочного среднего , ,…, - реализация случайной выборки (1). 3. Свойства выборочного среднего а) б)

Слайд 16

Описание слайда:

II. Выборочная дисперсия Опр. Выборочной дисперсией, построенной по случайной выборке (1), называется с.в

Слайд 17

Описание слайда:

Формула для вычисления выборочной дисперсии по реализации (2) .

Слайд 18

Описание слайда:

2. Свойства выборочной дисперсии . В определении взят множитель вместо для того, чтобы добиться важного свойства несмещенности оценки .

Слайд 19

Описание слайда:

§4. Несмещенные, состоятельные и эффективные оценки Определение 1. Оценка параметра называется несмещенной, если для любого В противном случае оценка называется смещенной. Определение 2. Оценка называется состоятельной, если она сходится по вероятности к истинному значению параметрапри неограниченном возрастании объема выборки , т.е. для Показателем точности оценки служит дисперсия: чем дисперсия меньше, тем оценка лучше. С дисперсией оценки связано ее свойство эффективности. Определение 3. Эффективная оценка – это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра. Например, если то выборочные среднее и дисперсия эффективные оценки параметров и .

Слайд 20

Описание слайда:

§ 5. Выборочные моменты. Опр. 1. Моментом порядка случайной величины наз-ся число Опр. 2. Выборочным моментом порядка , построенным по случайной выборке (1), наз. случайная величина Опр. 3. Центральным моментом порядка случайной величины наз. число Опр. 4. Выборочным центральным моментом порядка , построенным по случайной выборке (1), наз. случайная величина

Слайд 21

Описание слайда:

Характеристики формы распределения Для симметричных относительно мат. ожидания распределений =0. Если >0, то кривая распределения более полога справа от моды. Если 0, то график плотности имеет более острую и высокую вершину, чем нормальная кривая. Если < 0, то график плотности имеет более плоскую и низкую вершину, чем нормальная кривая.

Слайд 22

Описание слайда:

. При проведении статистического анализа важно знать, насколько близок закон распределения выборки к нормальному. Выборочные асимметрия и эксцесс характеризуют степень отличия эмпирического распределения от нормального. Коэффициент асимметрии и эксцесс нормального распределения равны нулю. Поэтому, достаточно малые значения соответствующих выборочных величин дают основание предполагать, что генеральная совокупность распределена по нормальному закону. Для первоначальной проверки выборки на соответствие нормальному закону можно применить экспресс-метод [6]: предположение о близости выборочного распределения к нормальному отвергается при условии ≥. Величина называется коэффициентом вариации. Замечание. Для нахождения выборочных характеристик могут быть использованы встроенные функции категории «статистические» из электронных таблиц Excel. Средство Excel ОПИСАТЕЛЬНАЯ СТАТИСТИКА позволяет вычислить важнейшие числовые характеристики выборки и представить их в виде таблицы.