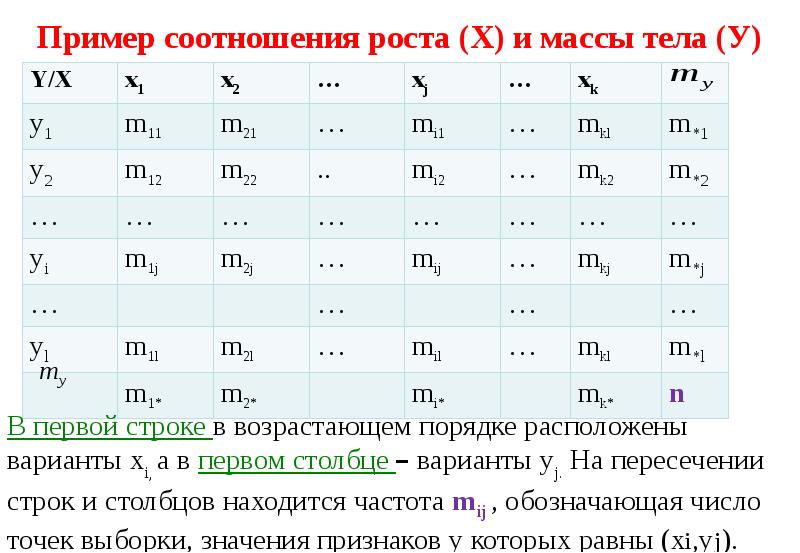
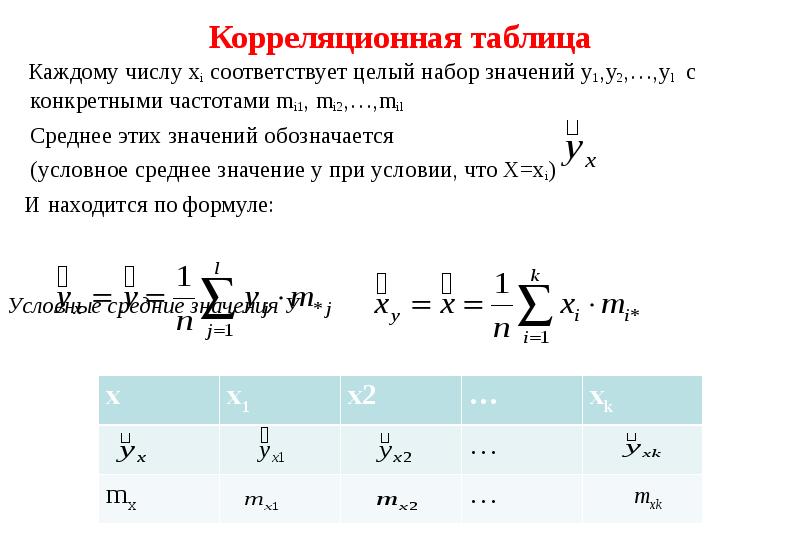
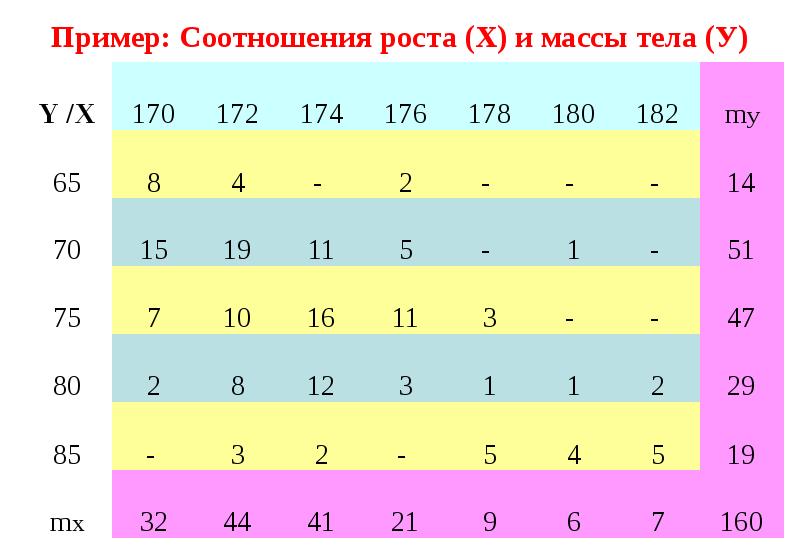
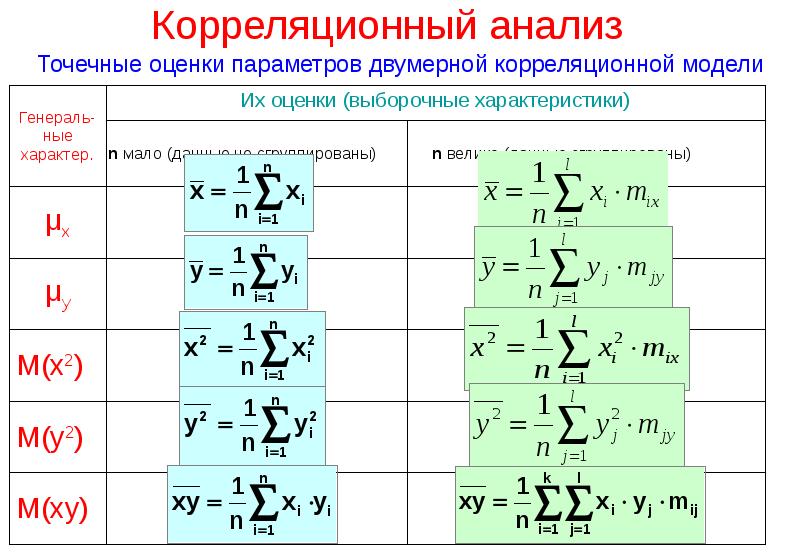
Готовые презентации на тему:
- Образование
- Искусство и Фото
- Наши презентации
- Авто/мото
- Технологии
- Бизнес и предпринимательство
- Карьера
- Данные и аналитика
- Дизайн
- Устройства и комплектующие
- Экономика и Финансы
- Машиностроение
- Развлечения и Юмор
- Путешествия
- Eда
- Политика
- Юриспруденция
- Здоровье и Медицина
- Интернет
- Инвестиции
- Закон
- Стиль жизни
- Маркетинг
- Мобильные технологии
- Новости
- Недвижимость
- Рекрутинг
- Розничная торговля
- Таможня, ВЭД, Логистика
- Наука
- Услуги
- Программное обеспечение
- Спорт
- Музыка
- Шаблоны презентации
- Детские презентации
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- История
- Литература
- Информатика
- Математика
- Обществознание
- Русский язык
- Физика
- Философия
- Химия
- МХК
- ОБЖ
- Окружающий мир
- Педагогика
- Технология
- Начальная школа
- Раскраски для детей
- Товароведение
- Менеджмент
- Страхование










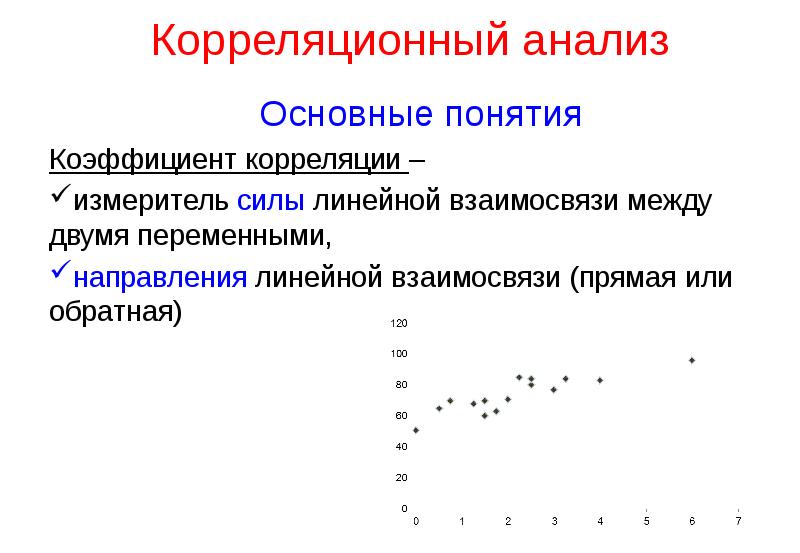










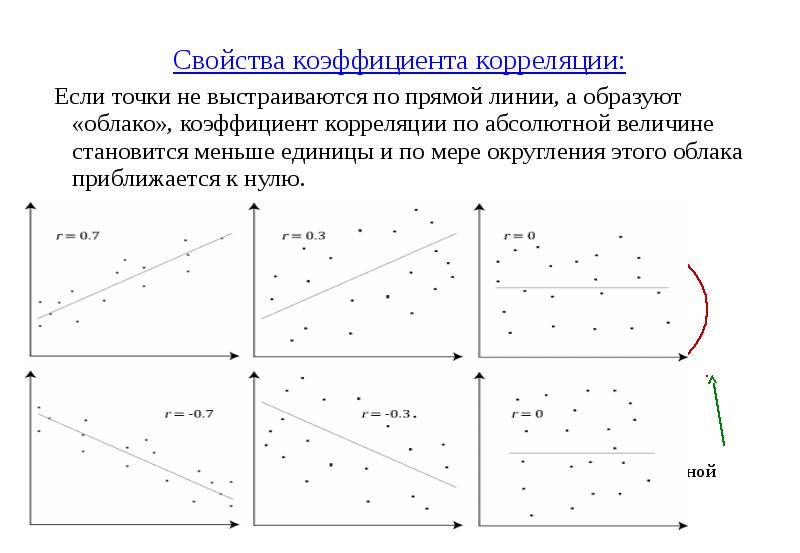
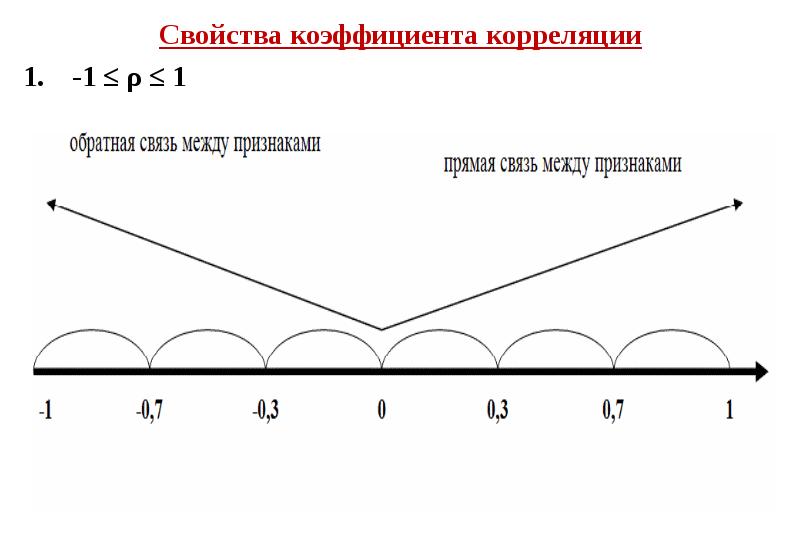


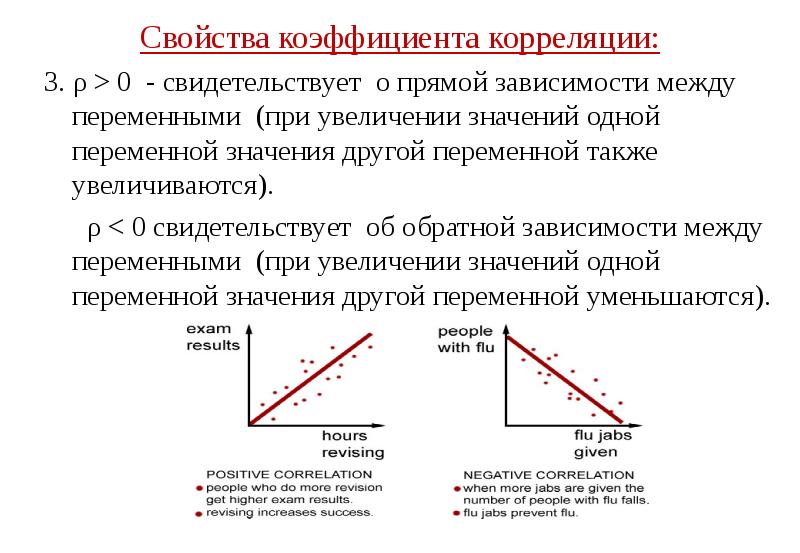
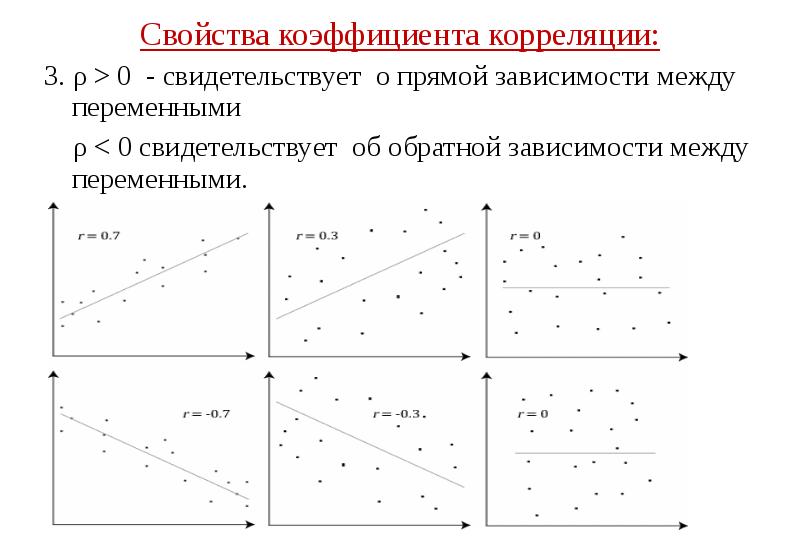







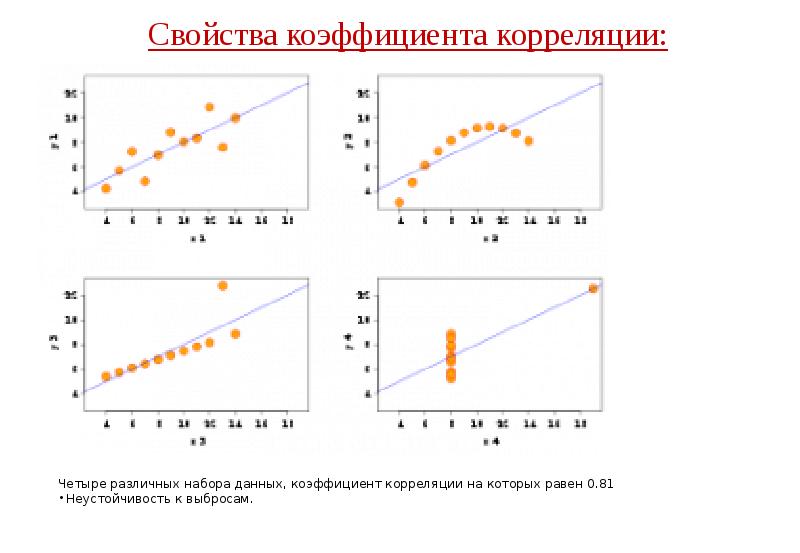
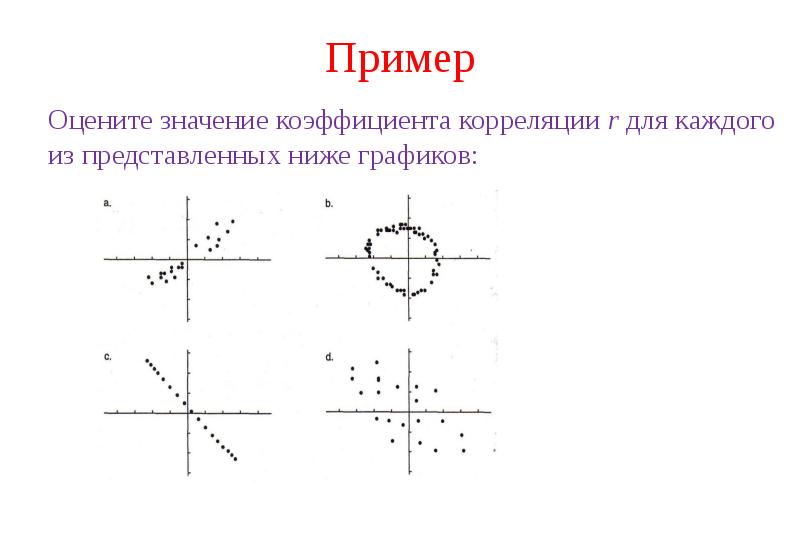
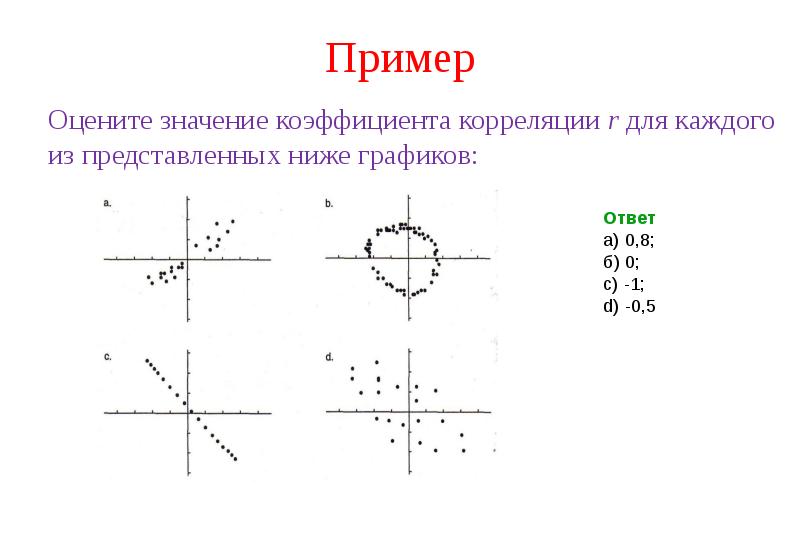


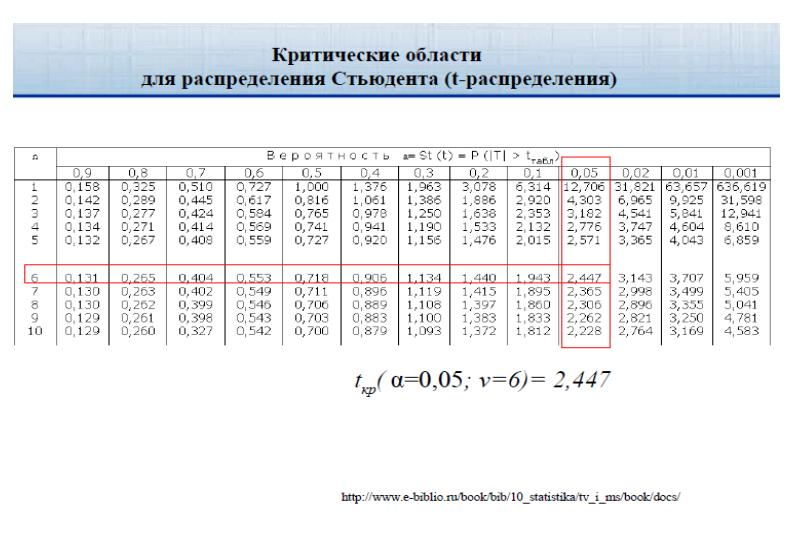








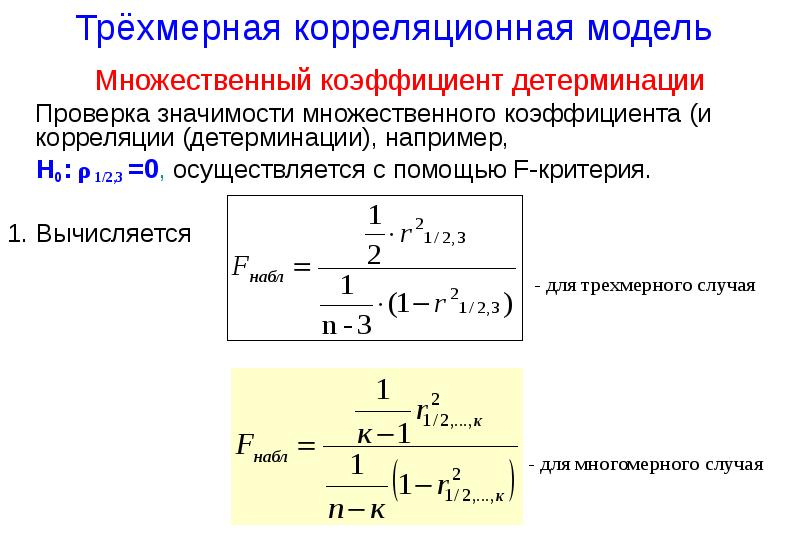
![Трёхмерная корреляционная модель
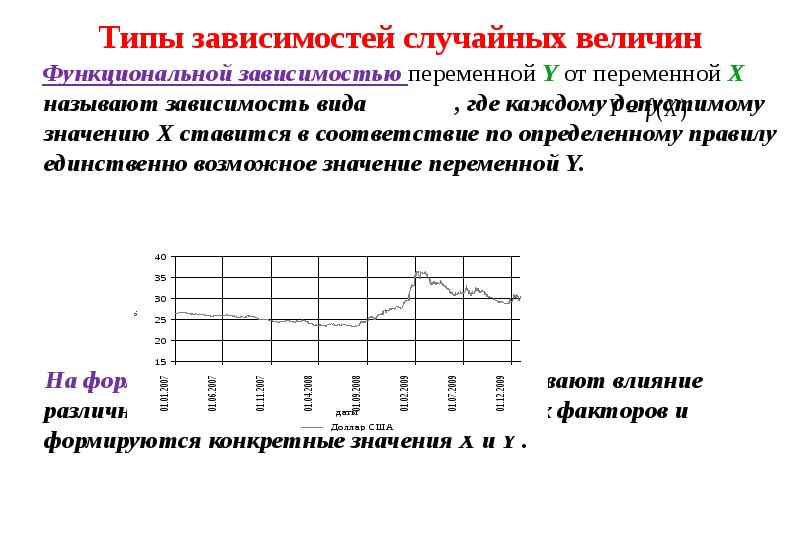
Пусть признаки X, Y, Z образуют трехмерную нормально распределенную генеральную совокупность, которая определяется девятью параметрами:
(X,Y,Z) ↔ N(μx ,μy ,μz ,σx ,σy ,σz ,ρxy ,ρyz ,ρxz)
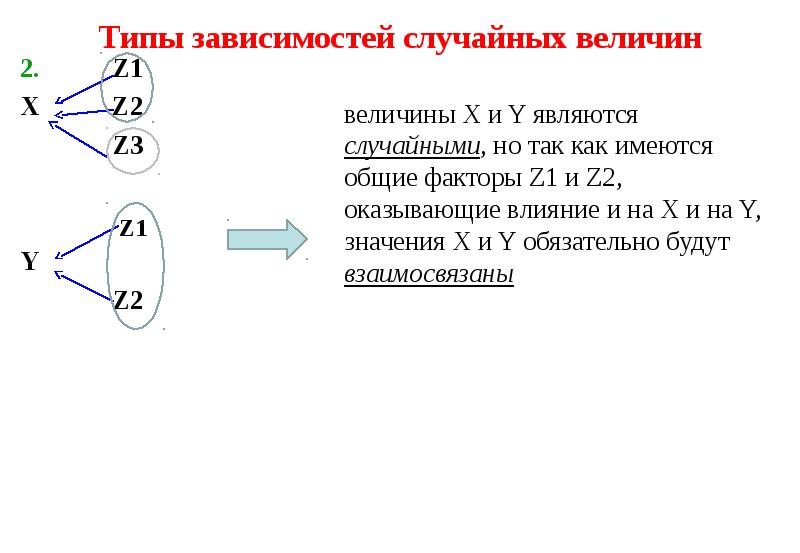
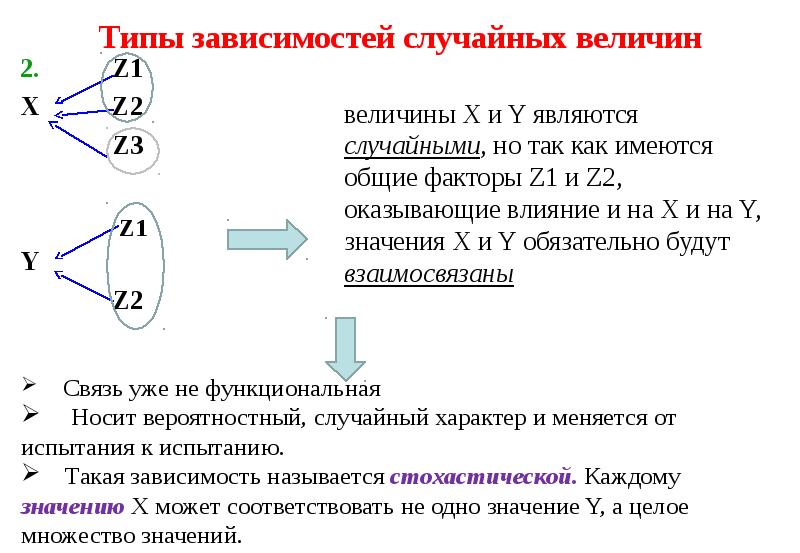
! Одномерные распределения X, Y, Z
и двумерные [(X, Y), (X,Z), (Y, Z)] распределения компонент,
а так же условные распределения при фиксированных одной [(X,Y)/Z; (X,Z)/Y; (Y,Z)/X]
и двух переменных [X/(Y,Z); Y/(X,Z); z/(X,Y)]
являются нормальными. Поэтому поверхности и линии регрессии являются плоскостями и прямыми соответственно.](/documents_6/1f74cd5cc33fa9fe0465fd53d408f5a7/img63.jpg)