Обратные тригонометрические функции - презентация, доклад, проект скачать

Нажмите для полного просмотра!

Обратные тригонометрические функции, слайд №1

Обратные тригонометрические функции, слайд №2

Обратные тригонометрические функции, слайд №3

Обратные тригонометрические функции, слайд №4

Обратные тригонометрические функции, слайд №5

Обратные тригонометрические функции, слайд №6

Обратные тригонометрические функции, слайд №7

Обратные тригонометрические функции, слайд №8

Обратные тригонометрические функции, слайд №9

Обратные тригонометрические функции, слайд №10

Обратные тригонометрические функции, слайд №11

Обратные тригонометрические функции, слайд №12

Обратные тригонометрические функции, слайд №13

Обратные тригонометрические функции, слайд №14

Обратные тригонометрические функции, слайд №15

Обратные тригонометрические функции, слайд №16

Обратные тригонометрические функции, слайд №17

Обратные тригонометрические функции, слайд №18

Обратные тригонометрические функции, слайд №19

Обратные тригонометрические функции, слайд №20

Обратные тригонометрические функции, слайд №21

Обратные тригонометрические функции, слайд №22

Обратные тригонометрические функции, слайд №23

Обратные тригонометрические функции, слайд №24

Обратные тригонометрические функции, слайд №25

Обратные тригонометрические функции, слайд №26

Обратные тригонометрические функции, слайд №27

Обратные тригонометрические функции, слайд №28

Обратные тригонометрические функции, слайд №29

Обратные тригонометрические функции, слайд №30

Обратные тригонометрические функции, слайд №31

Обратные тригонометрические функции, слайд №32

Обратные тригонометрические функции, слайд №33

Обратные тригонометрические функции, слайд №34

Обратные тригонометрические функции, слайд №35

Обратные тригонометрические функции, слайд №36

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему Обратные тригонометрические функции. Доклад-сообщение содержит 36 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Обратные тригонометрические функции

Слайд 2

Описание слайда:

Историческая справка Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу тригонометрическими функциями, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции – Евклида, Архимеда, Аполлония Пергского и других. В последующий период математика долгое время наиболее активно развивалась индийскими и арабсками учеными. В трудах по астрономии Ариабхаты появляется термин «ардхаджива». Позднее привилось более краткое название «джива», а при переводе математических терминов в XII в. Это слово было заменено латинским «sinus». Принципиальное значение имело составление Птолемеем первой таблицы синусов(долгое время она называлась таблицей хорд): появилось практическое средство решения ряда прикладных задач, и в первую очередь задач астрономии. Слово косинус –это сокращение латинского выражения «complementy sinus»(синус). Тангенсы возникли в связи с решением задачи об определении длины тени.Тангенс (а также котангенс, секанс и косеканс) введен в X веке Абу-л-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты в XIV в. Т. Бравердином, а позже астрономом Региомонтаном. Первым автором, который использовал специальные символы для обратных тригонометрических функций был, Бернулли. В 1729 и в1736 годах он писал as и at соответственно вместо arcsin и arctg.Современные обозначения arcsin и arctg появляются в 1772 г. в работах венского математика Шерфера известного французского ученого Лагранжа.Приставка «arc» происходит от латинского «arcus»(лук, дуга), что вполне согласуется со смыслом понятия: arcsin x, например,- это угол (а можно сказать и дуга) синус которого равен x.

Слайд 3

Описание слайда:

Для тригонометрических функций можно определить обратные функции (круговые функции, аркфункции). Они обозначаются соответственно , , , . Для тригонометрических функций можно определить обратные функции (круговые функции, аркфункции). Они обозначаются соответственно , , , .

Слайд 4

Описание слайда:

Почему можно определить обратную тригонометрическую функцию. Теорема о корне: Пусть функция f возрастает (или убывает) на промежутке I, число a – любое из значений, принимаемых f на этом промежутке. Тогда уравнение F(x)=a имеет единственный корень в промежутке I. На промежутке функция монотонна, возрастает, т.е. все значения от -1 до 1 принимает ровно один раз, поэтому можно определить обратную функцию - arcsin x. На промежутке функция монотонна, убывает, т.е. принимает все значения от -1 до 1 ровно один раз, поэтому можно определить обратную тригонометрическую функцию. На интервале функция монотонна, возрастает и принимает все значения из R ровно один раз, поэтому можно определить обратную тригонометрическую функцию. На интервале функция монотонна, убывает , принимает все значения из R ровно один раз, поэтому мы можем определить обратную тригонометрическую функцию.

Слайд 5

Описание слайда:

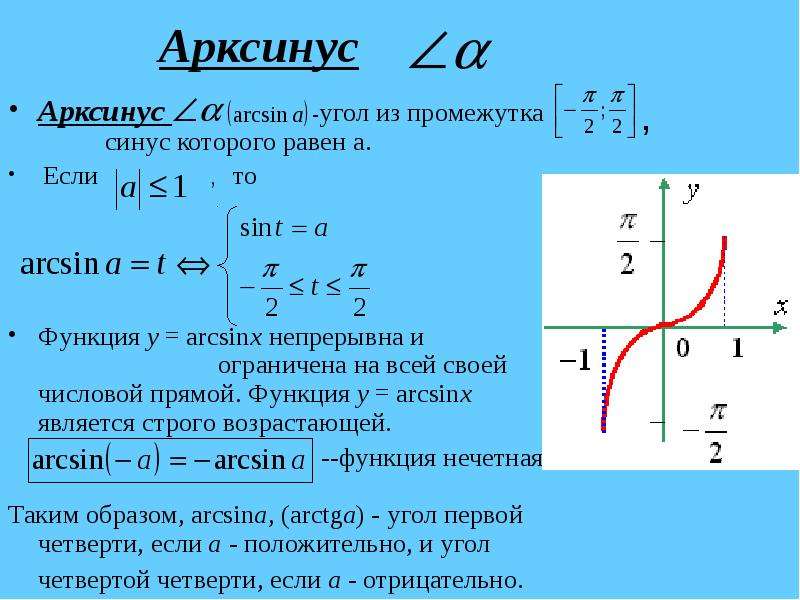
Арксинус Арксинус -угол из промежутка синус которого равен а. Если , то Функция y = arcsinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей. --функция нечетная Таким образом, arcsina, (arctga) - угол первой четверти, если a - положительно, и угол четвертой четверти, если a - отрицательно.

Слайд 6

Описание слайда:

Арккосинус Арккосинус -угол из промежутка , косинус которого равен а. Если , то Функция y = arccosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей. arccosa (arctga) - угол первой четверти, если a - положительно, и угол второй четверти, если a - отрицательно.

Слайд 7

Описание слайда:

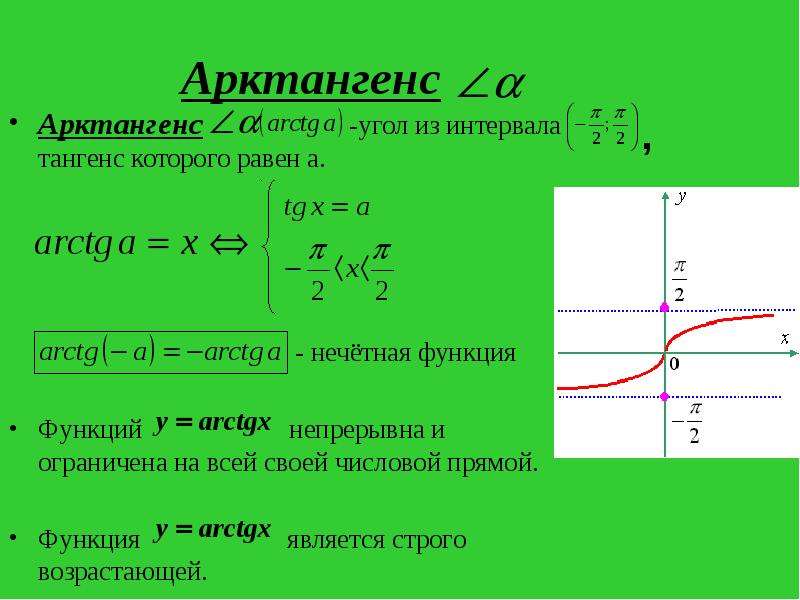
Арктангенс Арктангенс -угол из интервала тангенс которого равен а. - нечётная функция Функций непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Слайд 8

Описание слайда:

Арккотангенс Арккотангенс -угол из интервала , котангенс которого равен а.

Слайд 9

Описание слайда:

Преобразований сумм обратных тригонометрических функций

Слайд 10

Описание слайда:

Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность( функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения). Поэтому справедливы следующие равносильные переходы.

Слайд 11

Описание слайда:

Примеры Пример 1. Решить уравнение Решение. Уравнение равносильно системе:

Слайд 12

Описание слайда:

Пример 2. Решить неравенство 3arcsin 2x < 1. Пример 2. Решить неравенство 3arcsin 2x < 1. Решение.

Слайд 13

Описание слайда:

Слайд 14

Описание слайда:

Пример 3. Решить неравенство Пример 3. Решить неравенство Решение.

Слайд 15

Описание слайда:

Пример 4. Решить уравнение Пример 4. Решить уравнение Решение. Так как , то имеет место следующая цепочка равносильных преобразований:

Слайд 16

Описание слайда:

III а) arctg f(x) = arctg g(x) f(x) = g(x); б) acrtg f(x) ≤ arctg g(x) f(x) ≤ g(x).

Слайд 17

Описание слайда:

Пример 5. Решить неравенство Пример 5. Решить неравенство Решение. Неравенство равносильно следующему:

Слайд 18

Описание слайда:

Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x0 – решение этого уравнения. Обозначим arcsin f(x0) = arccos g(x0) через a. Тогда sin a = f(x0), cos a = g(x0), откуда Итак, arcsin f(x) = arccos g(x) (1)

Слайд 19

Описание слайда:

Рассуждая аналогично, можно получить следующие переходы:

Слайд 20

Описание слайда:

Примеры

Слайд 21

Описание слайда:

Пример 7. Решить уравнение Решение. Корень x = – 2 является посторонним. Ответ:

Слайд 22

Описание слайда:

Пример 8. Решить уравнение arctg (2sin x) = arcctg (cos x). Решение. Корни вида являются посторонними. Ответ:

Слайд 23

Описание слайда:

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций. При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций. Пример 9. Решить неравенство Решение. Рассмотрим функцию и решим неравенство f(x) ≤ 0 методом интервалов. 1) Найдем D(f). Для этого решим систему 2) Найдем нули f(x). Для этого решим уравнение Корень x = – 2 является посторонним

Слайд 24

Описание слайда:

3) Решим неравенство f(x) ≤ 0 методом интервалов.

Слайд 25

Описание слайда:

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например, При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Слайд 26

Описание слайда:

Замена переменной Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Слайд 27

Описание слайда:

Пример 11. Решить неравенство Решение. Пусть arccos x = t, 0 ≤ t ≤ . Тогда Поскольку откуда Ответ: [– 1; cos 2] И[cos 1; 1]. Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Слайд 28

Описание слайда:

Пример 12. Пример 12. Решить уравнение Решение. Данное уравнение равносильно следующему: Пусть arcsin x = t, Тогда

Слайд 29

Описание слайда:

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы. Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения. Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения. Теорема 3. Если то на множестве X уравнение f(x) = g(x) равносильно системе

Слайд 30

Описание слайда:

Пример 13. Решить уравнение 2arcsin 2x = 3arccos x. Пример 13. Решить уравнение 2arcsin 2x = 3arccos x. Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный. Ответ: {0,5}. Пример 14. Решить уравнение Решение. Пусть Тогда уравнение примет вид Функции являются монотонно возрастающими. Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому Ответ: {– 1; 0}.

Слайд 31

Описание слайда:

Пример 15. Решить неравенство Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок Ответ:

Слайд 32

Описание слайда:

Пример 16. Решить уравнение Пример 16. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = . Решение. Поскольку arcsin то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно Таким образом, уравнение равносильно системе: Решение последней системы не представляет труда.

Слайд 33

Описание слайда:

Уравнения и неравенства с параметрами. Пример 1. Решить уравнение с параметром a: Решение. Уравнение равносильно уравнению Рассмотрим два случая: 1) a = 0. В этом случае система примет вид: 2) a ≠ 0. В этом случае уравнение системы является квадратным. Его корни: Так как | x | ≤ 1, то Если a = – 1, то Если то уравнение имеет два корня. Ответ: при при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Слайд 34

Описание слайда:

Пример 2. Решить неравенство с параметром a: Пример 2. Решить неравенство с параметром a: Решение. Неравенство равносильно системе

Слайд 35

Описание слайда:

Пример 3. Решить уравнение с параметром a: Пример 3. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a). Решение. Данное уравнение равносильно системе Графиком квадратного трехчлена является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 < 0, то при любом a уравнение f(x) = 0 имеет ровно 2 корня, между которыми и заключено число 2a. Поэтому только больший корень f(x) удовлетворяет условию x > 2a. Это корень Ответ: при любом a

Слайд 36

Описание слайда:

Список используемой литературы 1. Коломогоров «алгебра начало анализа» 2. Вельмушкина, Н. Уравнения, содержащие обратные тригонометрические функции [Текст] / Н. Вельмушкина // Математика / Прил. к ПС, 2004. – №6. – С.26-27. 3. В.С. Крамор, П.А Михайлов " Тригонометрические функции ." Москва "Просвещение " 1983г. 4. В. Н. Литвиненко, А. Г. Мордкович . " Практикум по решению математических задач. " Москва "Просвещение " 1984г. 5. А.П. Ершова , В. В. Голобородько " Алгебра . Начала анализа. " "ИЛЕКСА " Москва 2003г 6. Кожеуров, П.Я. Тригонометрия [Текст] / П.Я. Кожеуров. – М.: Физматгиз, 1963. – 320с. 7. Савин, А. Тригонометрия [Текст] / А. Савин // Квант, 1996. – №4.