🗊Презентация Funktsiooni uurimine

Funktsiooni uurimine Koostas: E. Reila

1. Määramispiirkond X

2. Muutumispiirkond Y

3. Nullkohtade hulk X0

4. Funktsiooni positiivsuspiirkond X + ja negatiivsuspiirkond X -

5. Funktsiooni ekstreemumkohtade hulk Xe Funktsiooni ekstreemumkohtadeks nimetatakse funktsiooni maksimum- ja miinimumkohti.

6. Funktsiooni kasvamisvhemikud X ja kahanemisvahemikud X

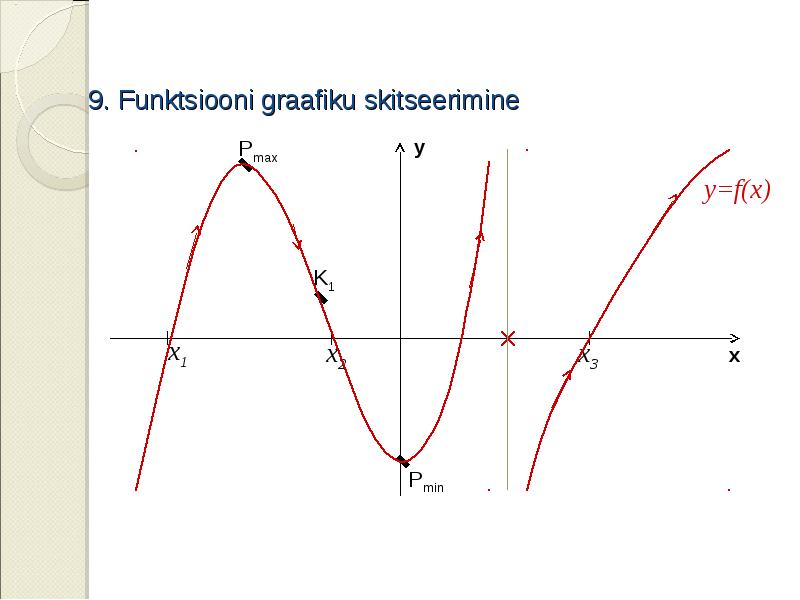
8.* Funktsiooni graafiku kumerusvahemikud X ja nõgususvahemikud X Funktsiooni y=f(x) graafikut nimetatakse kumeraks (nõgusaks) vahemikus ]a;b[, kui ükski tema punkt selles vahemikus ei ole kõrgemal (allpool) ühestki tema puutujast selles vahemikus

7.* Funktsiooni graafiku käänupunktide hulk Xk Funktsiooni käänupunktiks nimetatakse punkti, millest funktsiooni graafiku läbiminekul muutub kumerus nõgususeks või vastupidi.

9. Funktsiooni graafiku skitseerimine

Funktsiooni uurimise kokkuvõte: Selleks, et uurida funktsiooni, tuleb leida selle funktsiooni: 1. Määramispiirkond X 2. Muutumispiirkond Y 3. Nullkohtade hulk X0 : f(x)=0 4. Funktsiooni positiivsuspiirkond X + : f(x)>0 Funktsiooni negatiivsuspiirkond X -: f(x)<0 5. Funktsiooni ekstreemumkohtade hulk Xe: f ´(x)=0 funktsiooni ekstreemumpunktid Pe(xe;ye) 6. Funktsiooni kasvamisvhemikud : f ´(x)>0 Funktsiooni kahanemisvahemikud : f ´(x)<0 7.* Funktsiooni graafiku käänukohtade hulk Xk: f ´´(x)=0 funktsiooni käänupunktid K(xk;yk) 8.* Funktsiooni kumerusvahemikud : f ´´(x)<0 Funktsiooni nõgususvahemikud : f ´´(x)>0 9. Skitseerida funktsiooni graafik

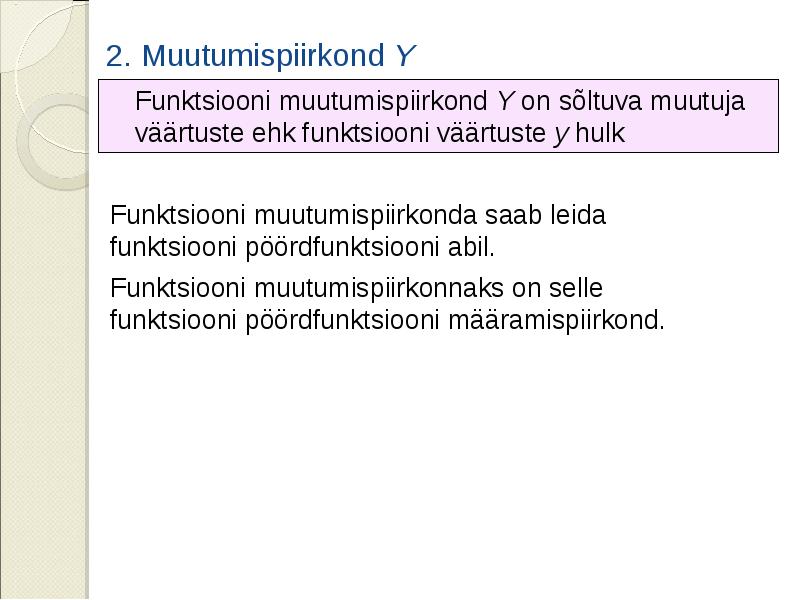
Näide Uuri funktsiooni y= x 3 - 6x 2 + 8x ja skitseeri funktsiooni graafik 1. Määramispiirkond X 2. Muutumispiirkond Y 3. Nullkohtade hulk x(x2 -6x +8)=0 ehk x(x-2)(x-4)=0 x1=0; x2=2; x3=4 X0={0; 2; 4} 4. Funktsiooni positiivsus- X + ja negatiivsusvahemikud X - X + =]0; 2[ U ]4; [ X - =] - ;0[U]2; 4[

5. Funktsiooni ekstreemumkohtade hulk Xe 5. Funktsiooni ekstreemumkohtade hulk Xe f ´(x)=3x2-12x+8 3x2-12x+8=0 Xe={0,9; 3,2}; Pmax(0,9;3,1); Pmin(3,2;-3,1) 6. Funktsiooni kasvamisvhemikud X ja kahanemisvahemikud X X =]- ;0,9[ U ]3,2; [; X =]0,9;3,2[ 7. Funktsiooni graafiku käänukohtade hulk Xk f ´´(x)=6x-12 6x-12 =0 xk=2 yk=23 - 6 22 + 8 2 = 0 Xk={2}; K(2;0) 8. Funktsiooni kumerusvahemikud ja nõgusus vahemikud =]- ;2[; =]2; [

9. Funktsiooni graafiku skitseerimine