🗊Презентация Matlab. Математические вычисления

Содержание Введение Основы Matlab Вычисления в Matlab Функции для работы с массивами Графические возможности Matlab Программирование в Matlab Аналитические вычисления в Matlab

Matlab (MATrix LABoratory) – это математические вычисления создание алгоритмов моделирование анализ, обработка и визуализация данных научная и инженерная графика разработка приложений с GUI огромное количество прикладных пакетов

Пакеты, встроенные в Matlab Matlab Web Server Bioinformatics Toolbox Communications Toolbox Control System Toolbox Database Toolbox Distributed Computing Toolbox Financial Toolbox Fuzzy Logic Toolbox Genetic Algorithm and Direct Search Toolbox Image Processing Toolbox Neural Networks Toolbox Partial Differential Equation Toolbox Signal Processing Toolbox

ОСНОВНЫЕ ЧАСТИ ПАКЕТА MATLAB: Язык Matlab Среда Matlab Управляемая графика Библиотека математических функций Программный интерфейс

Язык Matlab Си- и Паскаль-подобный объектно-ориентированный Огромный набор встроенных функций Расширяемый пользователем

Среда Matlab Интерактивная работа Управление переменными в рабочем пространстве Редактор Отладчик

Управляемая графика Команды высокого уровня для работы с 2D- и 3D-графикой Анимация Команды низкого уровня для работы с графикой

Библиотека математических функций Обширная коллекция вычислительных алгоритмов от элементарных функций (sin, cos и т. п.) до более сложных обращение матриц вычисление собственных значений минимизация функций дифференцирование интегрирование и пр.

Программный интерфейс API для взаимодействия с программами на языках Си и Фортран

Matlab – язык для работы с матричными объектами Основной объект Matlab – матрица Число – это матрица размера (1x1) Использование матриц существенно облегчает программирование делает запись формул краткой и наглядной В дальнейшем изложении предполагается знакомство с матричной алгеброй и основами программирования

Числа Основной базовый тип для матриц Хранятся в формате long (double) стандарт плавающей точки IEEE Интервал приблизительно от 10E-308 до 10E+308 Комплексные числа строятся с применением суффиксов i или j (мнимая единица): 2.4e7+3.005i

Другие типы Строки Массивы структур (записей) Массивы ячеек позволяют объединять в массиве элементы разной природы Объекты

Переменные и выражения Переменные определяются пользователем при помощи оператора присваивания: x=5 В левой части – имя переменной заглавные и строчные буквы различаются В правой части оператора присваивания может стоять выражение: y=(2-x)/(x+3) Если выражение встречается вне оператора присваивания, то его значение вычисляется и помещается в системную переменную ans (от answer) Переменную ans можно использовать для задания новых выражений: z=ans*3 Если оператор присваивания завершить символом «;», то результат на экране не дублируется; в противном случае – выводится на экран:

Операторы При составлении выражений могут быть использованы операторы: + сложение - вычитание * умножение / деление ^ возведение в степень Приоритет операций обычный. Изменяется при помощи круглых скобок

Операции отношения

Логические операции

Командная строка Простейший способ взаимодействия с Matlab – работа в командной строке (в режиме калькулятора) строка начинается с приглашения: символа >> Перемещение по стеку ранее введённых команд – клавиши ↑ и ↓ Для удобства размещения данных в КС можно разбивать вводимое выражение знаком «…» Очистить командное окно можно комадной clc

Работа с КС упрощается благодаря окну Command History (меню Desktop) Работа с КС упрощается благодаря окну Command History (меню Desktop) Здесь хранится сессионная запись всех введённых команд Их можно скопировать, выполнить и т. п. (см. контекстное меню)

Рабочее пространство (Workspace) Все переменные хранятся в РП порой это отнимает много места Просмотреть список существующих в РП переменных можно командой who:

Более подробную информацию о переменных РП можно вывести командой whos: Более подробную информацию о переменных РП можно вывести командой whos:

После закрытия сеанса работы MATLABа все переменные, вычисленные в течение сеанса, теряются. Однако их можно сохранить для последующего использования в иных сеансах, сохранив содержимое РП в файле на диске После закрытия сеанса работы MATLABа все переменные, вычисленные в течение сеанса, теряются. Однако их можно сохранить для последующего использования в иных сеансах, сохранив содержимое РП в файле на диске командой меню: File \ Save Workspace As… командой Matlab: save

Команда save save – сохраняет все переменные в файл matlab.mat save filename – сохраняет все переменные в файл filename save filename x y z – сохраняет переменные x, y, z в файл filename (можно по маске: a*) save filename x y z -ASCII – сохраняет переменные x, y, z в файл filename в текстовом виде save('filename’, ‘a',‘b','-ASCII') – процедурная форма вызова команды параметры – в виде строк (в одинарных апострофах) Подробнее про эту и любую другую команду Matlab help <имя команды> или F1

Команда load Служит для загрузки ранее сохранённых данных load – загружает все переменные из файла matlab.mat load filename – загружает все переменные из файла filename load filename x y z – загружает переменные x, y, z из файла filename load -ASCII filename x y z– загружает переменные x, y, z из текстового файла filename load('filename’, ‘a',‘b','-ASCII') – процедурная форма вызова команды

Команда clear Служит для удаления переменных из РП clear – удаляет все переменные clear all – удаляет всё, включая классы, функции, скомпилированные файлы и пр. clear x y z – удаляет переменные x, y и z.

Рабочий каталог Все файлы (данные, функции и пр.), созданные пользователем сохраняются в текущем каталоге (Current Directory) Изменить текущий каталог можно командой cd <путь> в строке ввода Current Directory на панели инструментов: в окне Current Directory

Сохранение рабочей сессии diary – сохраняет лог текущей сессии (весь текстовый ввод и вывод) в файл По умолчанию – в файл diary в текущем каталоге diary filename или diary(‘filename’) – сохраняют сессию в указанном файле diary off / diary on – соответственно, приостанавливают и продолжают ведение лога diary – переключается между режимами on/off, если лог уже ведётся

ВЫЧИСЛЕНИЯ В MATLAB

Элементарные функции Тригонометрические sin cos tan cot asin acos atan acot

Элементарные функции Экспоненциальные exp log – ln log10 log2 sqrt nthroot(x, n)

Элементарные функции Округление и остатки fix – округление к нулю floor – округление к минус бесконечности ceil – округление к плюс бесконечности round – округление к ближайшему целому mod(x,y) – остаток от деления x на y без учёта знака (x - n*y, где n = floor(x/y)) rem(x,y) – остаток от деления x на y с учётом знака (x - n*y, где n = fix(x/y))

Элементарные функции Комплексные числа abs(z) – модуль комплексного числа z angle(z) – фаза z (в радианах) real(z) – действительная часть z imag(z) – мнимая часть z conj(z) – комплексно сопряжённое число для z complex(a,b) – конструирует комплексное число a+ib isreal(z) – возвращает истину, если z – действительное

Элементарные функции Просмотреть полный список элементарных функций можно командой help elfun

Константы pi – число pi Inf – бесконечность -Inf – минус бесконечность NaN (Not a Number) – нечисловое значение

Одномерные массивы Задание массива: a = [ -3 4 2]; a = [ -3, 4, 2]; Диапазоны: b = -3: 2 (b = -3 -2 -1 0 1 2) b = -3:2:5 (b = -3 -1 1 3 5) Доступ к элементу: a(3) (будет равно 2) Изменение элемента: a(3) = 1 Количество элементов в массиве: length(a) (будет равно 3)

Двумерные массивы Задание массива: a = [ 1 2; 3 4; 5 6];

Векторы-столбцы и векторы-строки Любая строка и столбец матрицы – это вектор Векторы, расположенные вдоль строк – векторы-строки (размер 1xn) Векторы, расположенные вдоль столбцов – векторы-столбцы (размер nx1) Задание вектора-столбца: К векторам любого типа применима функция length

Размерность и размер матриц Размерность массива определяется функцией ndims(A)

Конкатенация Рассмотрим две матрицы

Диапазоны Можно использовать как для задания значений векторов, так и для задания диапазонов индексации Рассмотрим другие примеры

Для обращения к последнему элементу любой размерности можно использовать служебное слово end: Для обращения к последнему элементу любой размерности можно использовать служебное слово end:

Удаление строк и столбцов

Перестановка элементов

ФУНКЦИИ ДЛЯ РАБОТЫ С МАССИВАМИ В MATLAB

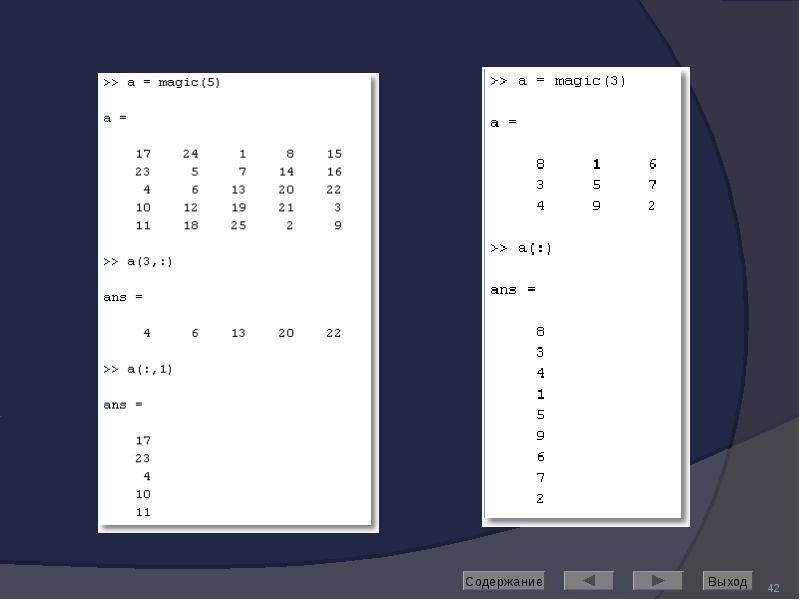
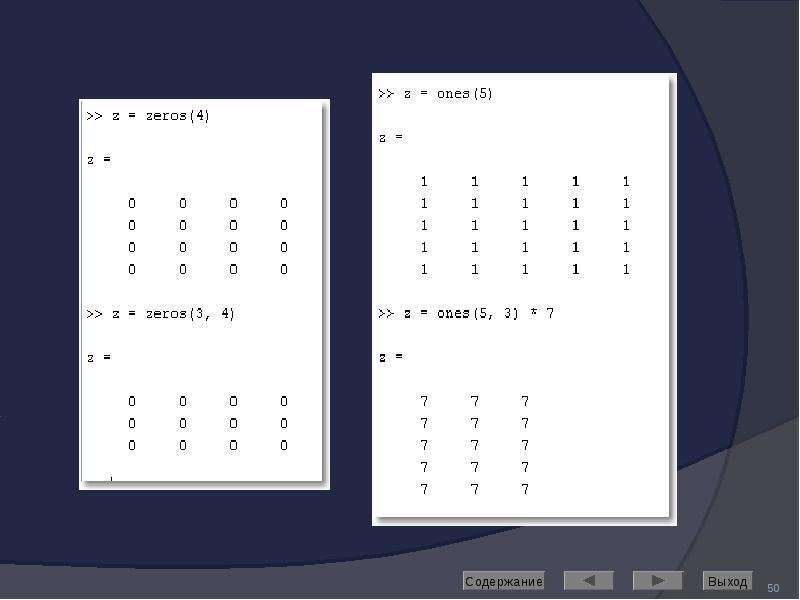
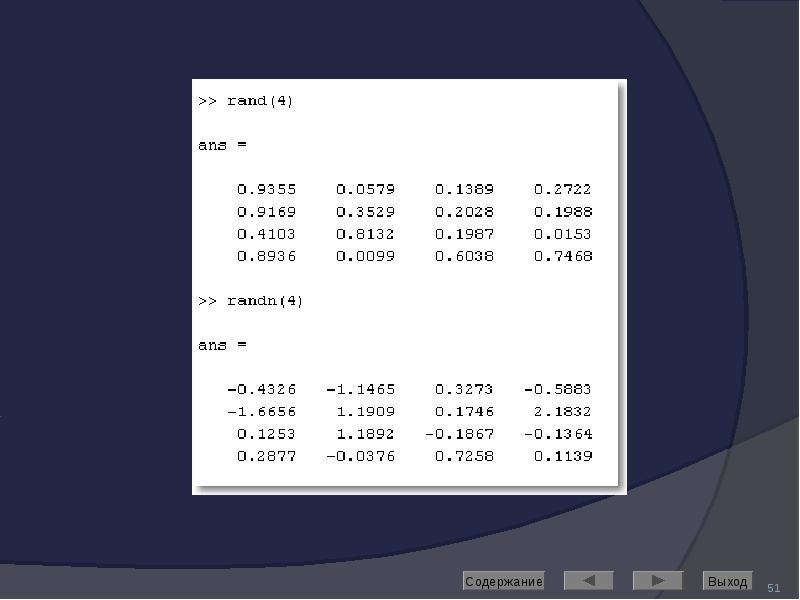
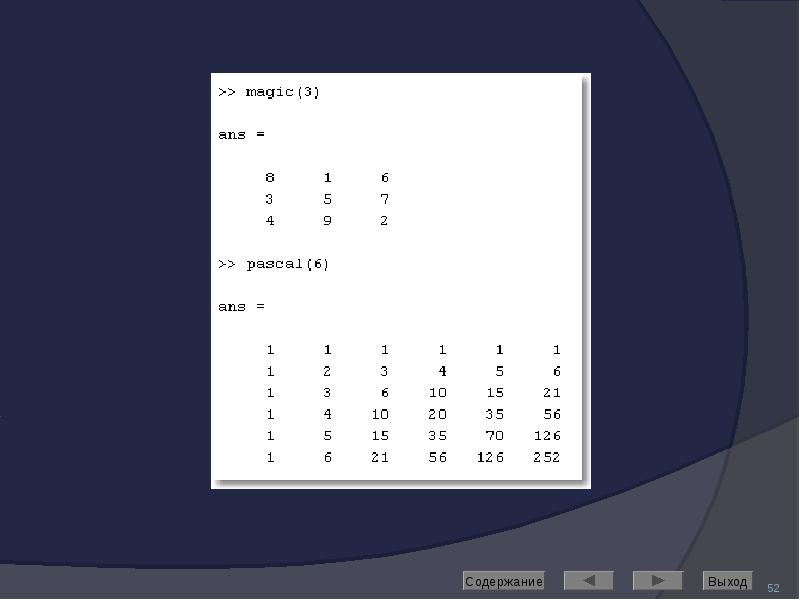
Создание матриц специального вида Для работы с матрицами удобно пользоваться следующими функциями ones – формирование массива из единиц zeros – формирование массива из нулей eye – формирование единичной матрицы rand – формирование матрицы из числе, равномерно распределённых на отрезке [0, 1] randn – формирование матрицы из чисел, нормально распределённых с математическим ожиданием 0. 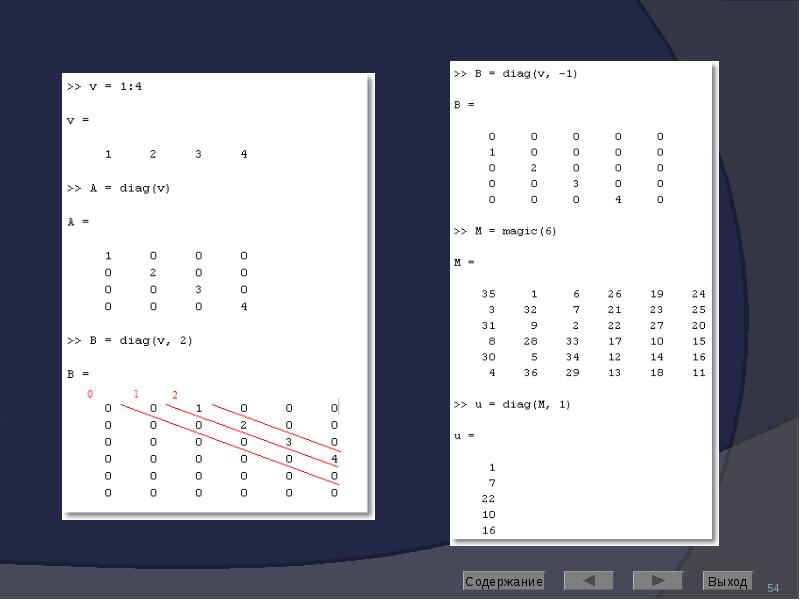magic – формирование магического квадрата pascal – формирование квадрата Паскаля diag – диагональная матрица и др.

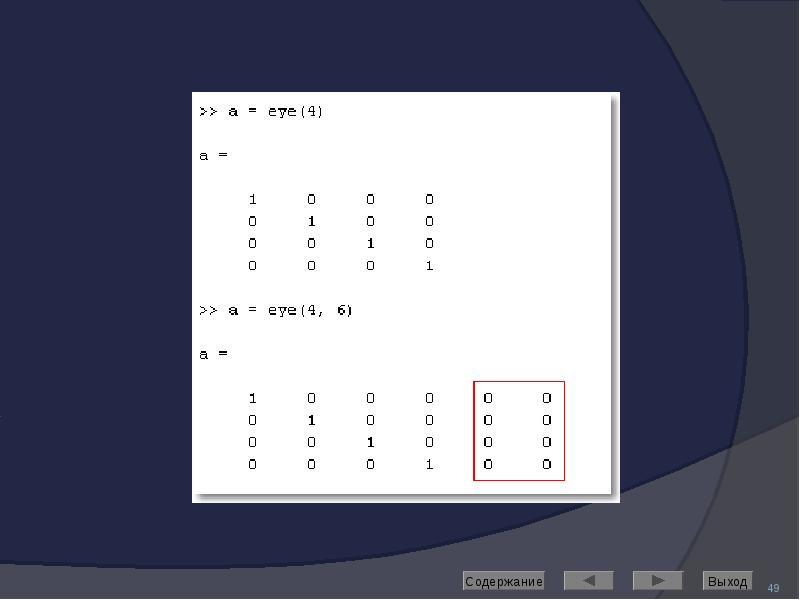
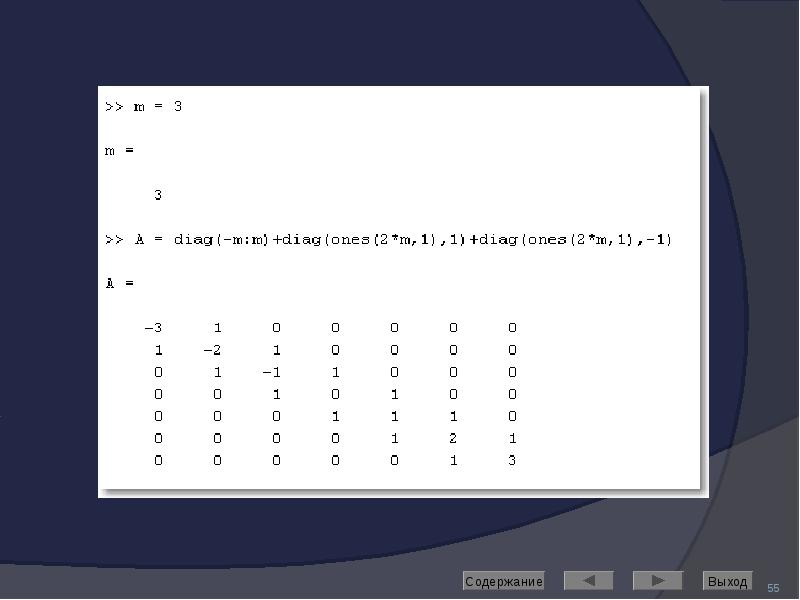
МАТРИЦЫ СПЕЦИАЛЬНОГО ВИДА Рассмотрим основной синтаксис на примере функции создания единичной матрицы (eye) eye(m) – создание единичной матрицы размера [m, m] eye(m, n) – создание единичной матрицы размера [m, n] «лишние» строки или столбцы дополняются нулями

Функция diag: работа с диагональными матрицами Функция diag: работа с диагональными матрицами у которых ненулевые элементы расположены на диагоналях Синтаксис: X = diag(v) – на главной диагонали матрицы X расположены элементы вектора v X = diag(v,k) – на k-ой диагонали матрицы X расположены элементы вектора v (по умолчанию k=0) v = diag(X,k) – извлечь из матрицы X k-ую диагональ и сохранить её в векторе v

ВЫЧИСЛЕНИЯ С ЭЛЕМЕНТАМИ МАССИВОВ Простейшие операции над элементами массивов: sum: сумма элементов prod: произведение элементов cumsum: кумулятивная сумма элементов cumprod: кумулятивное произведение элементов max: нахождение максимального элемента min: нахождение минимального элемента sort: сортировка элементов

Рассмотрим работу некоторых из этих функций на примере sum Рассмотрим работу некоторых из этих функций на примере sum Для векторов эта функция возвращает сумму элементов Для массивов – сумму элементов по каждому из столбцов результат – вектор-строка Остальные функции работают по этому же принципу

Кумулятивная сумма вычисляется так же, только происходит накопление вычисленных значений в элементах массива: Кумулятивная сумма вычисляется так же, только происходит накопление вычисленных значений в элементах массива:

Максимальный и минимальный элементы: Максимальный и минимальный элементы:

Вызов функций max/min с двумя выходными параметрами позволяет определить и индекс найденного элемента: Вызов функций max/min с двумя выходными параметрами позволяет определить и индекс найденного элемента:

Функция sort производит сортировку элементов матрицы по столбцам: Функция sort производит сортировку элементов матрицы по столбцам:

ЛОГИЧЕСКИЕ ФУНКЦИИ All(v) – возвращает истину, если все элементы вектора v отличны от нуля. Для матриц выдаёт вектор-строку с аналогичным результатом для каждого столбца

Any(v) – возвращает истину, если хотя бы один элемент вектора v отличен от нуля. Для матриц выдаёт вектор-строку с аналогичным результатом для каждого столбца Any(v) – возвращает истину, если хотя бы один элемент вектора v отличен от нуля. Для матриц выдаёт вектор-строку с аналогичным результатом для каждого столбца

Поиск в массиве find: определяет индексы элементов, удовлетворяющих заданному условию

Пример применения команды find к матрицам: Пример применения команды find к матрицам:

Математические матричные операции det – вычисление определителя квадратной матрицы

МАТРИЧНЫЕ И ПОЭЛЕМЕНТНЫЕ ОПЕРАЦИИ При работе с матрицами можно использовать два вида операторов: матричные: производят действия по правилам матричной алгебры поэлементные: производят действия над соответствующими элементами матриц размеры матриц должны быть одинаковыми от матричных операций отличаются точкой перед знаком операции

‘ транспонирование ‘ транспонирование + матричное (и поэлементное) сложение - матричное (и поэлементное) вычитание * матричное умножение / матричное деление ^ матричное возведение в степень

Такие операции часто используются, если нужно применить какую либо функцию ко всем элементам матрицы. Такие операции часто используются, если нужно применить какую либо функцию ко всем элементам матрицы.

Некоторые операции по умолчанию считаются поэлементными: Некоторые операции по умолчанию считаются поэлементными:

Операции «деления» слева и справа Применяются для решения систем линейных уравнений (СЛУ) Деление слева (\) для квадратных матриц реализует метод Гаусса для прямоугольных матриц– метод наименьших квадратов

ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ MATLAB

Графика в Matlab Высокоуровневая не требует от пользователя детальных знаний о работе графической подсистемы Объектная каждый объект на рисунке имеет свойства, которые можно менять Управляемая (handled) доступ к графическим объектам возможен как через инспектор объектов, так и при помощи встроенных функций (дескрипторная графика)

Двумерные (2D-) графики Простейший способ построения 2D-графика: задать область построения (диапазон); вычислить значение функции на области построения построить график при помощи одной из встроенных функций Matlab

Построение второго графика Если сразу же построить другой график, то старый график будет удалён из графического окна

Построение двух графиков в одной системе координат Два графика в одной СК можно построить следующими способами: «закрепить» графическое окно при помощи команды hold on применить одну команду plot

Пример закрепления графиков

Пример построения двух графиков одной командой

Дополнительные параметры команды plot В команде plot можно задать для каждого графика цвет линии тип маркера тип линии

Пример команды plot

Построение нескольких графиков в одном окне в разных СК Поверхность графического окна можно разделить на зоны, в каждой из которых выводить свой график Для этого служит команда subplot В качестве параметров ей передаётся трёхзначное целое число вида mnk m и n определяют количество графических «подокон» по горизонтали и вертикали k задаёт номер графического «подокна» порядок нумерации – по строкам

Первый subplot

Второй subplot

Построение графиков в разных графических окнах Создать новое графическое окно можно командой figure Команда figure создаёт графическое окно и возвращает указатель на него: h = figure Активизировать ранее созданное окно можно командой figure(h)

figure : пример использования 1

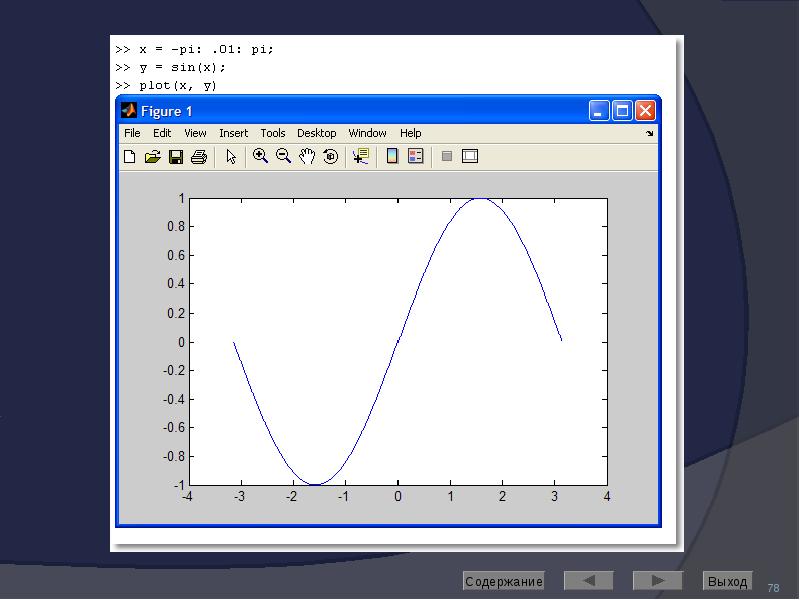
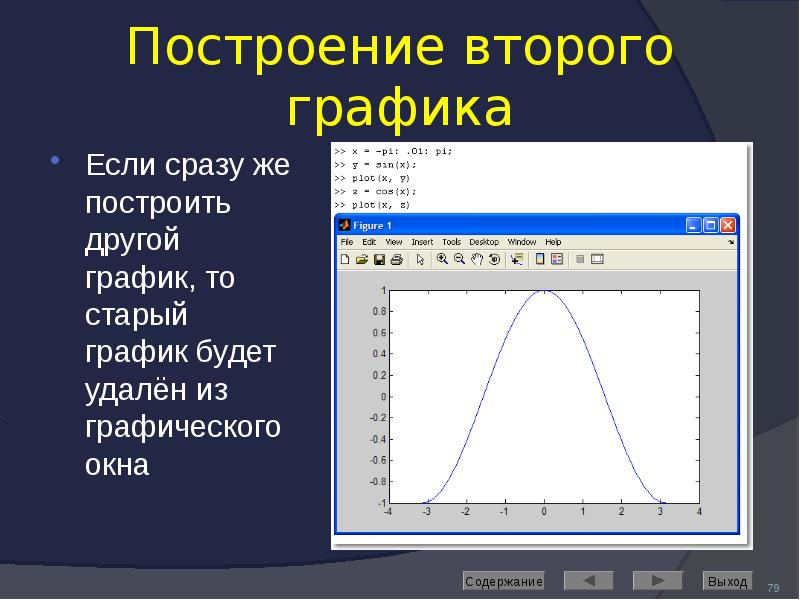
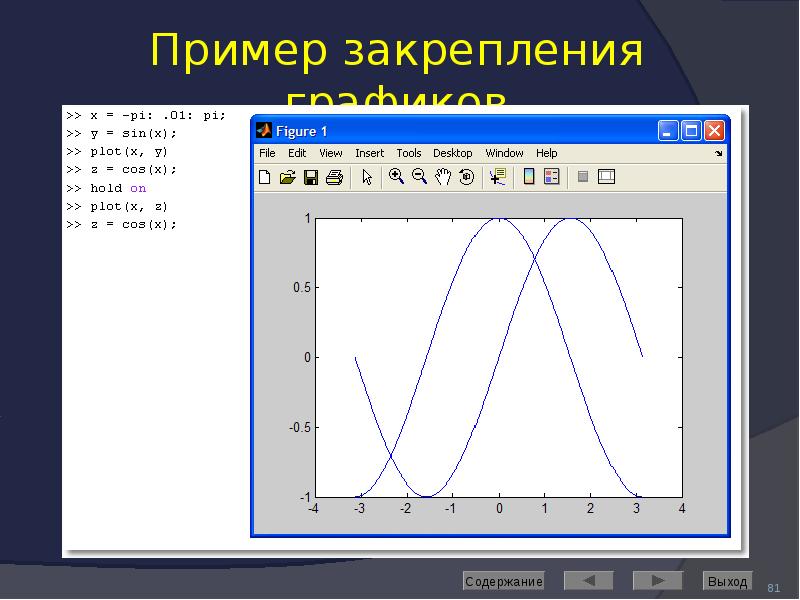
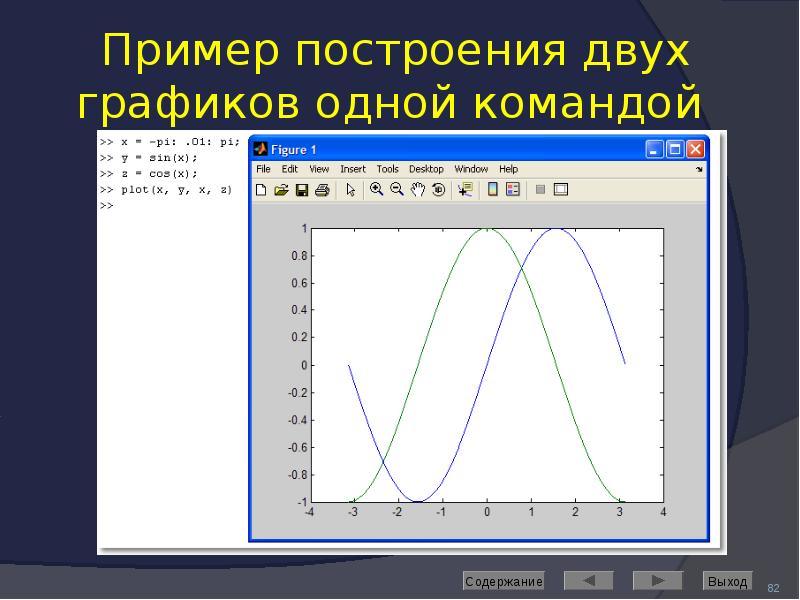
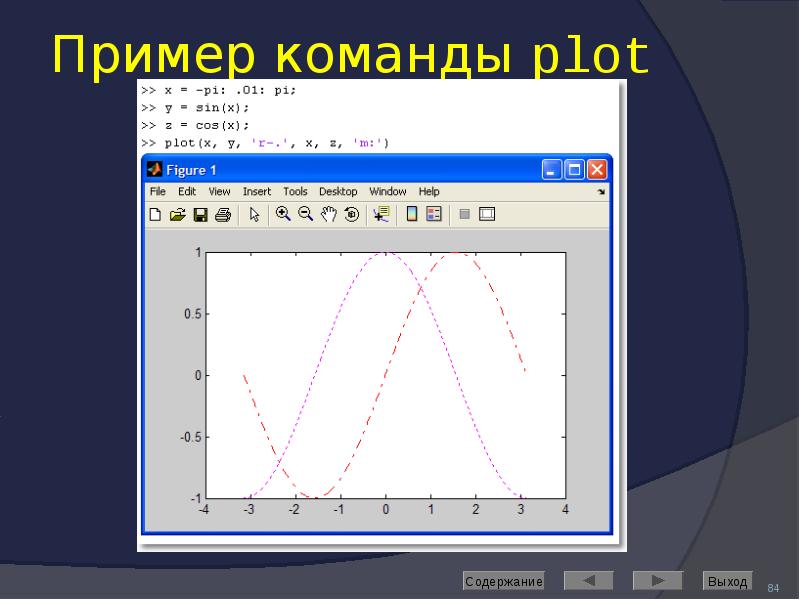
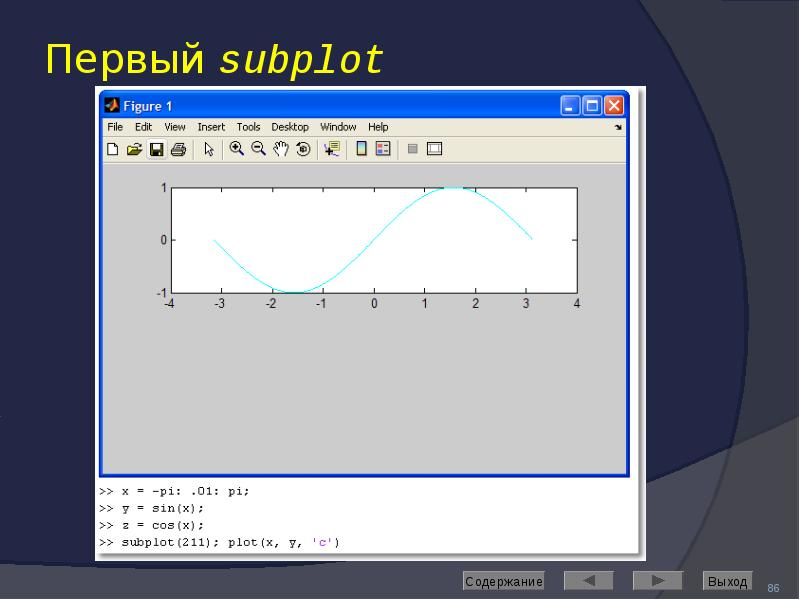
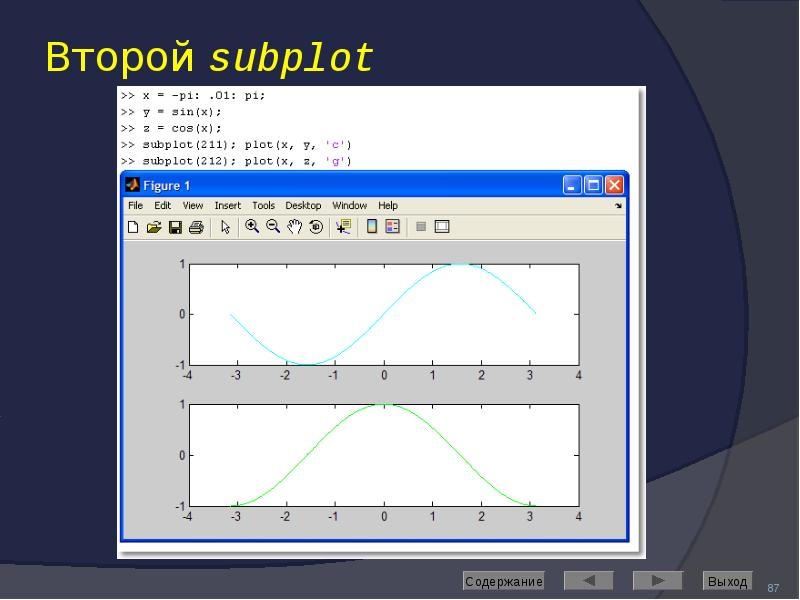
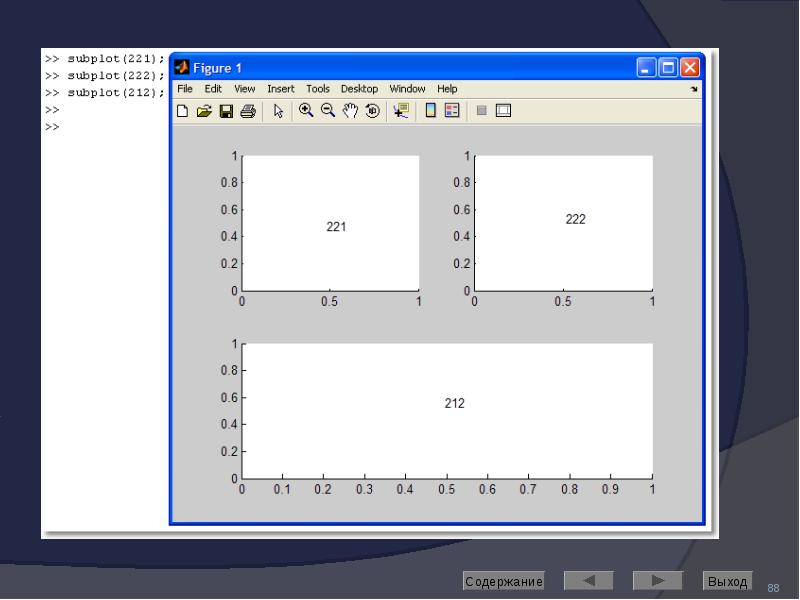
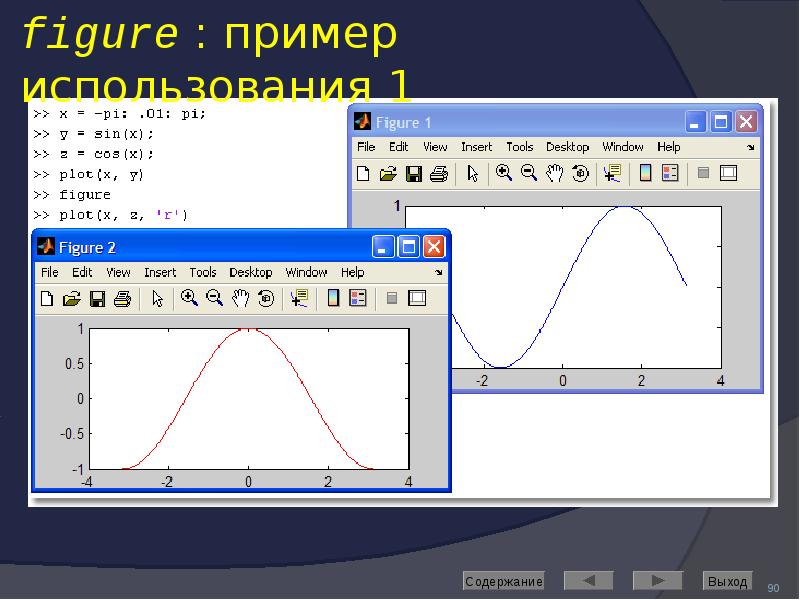
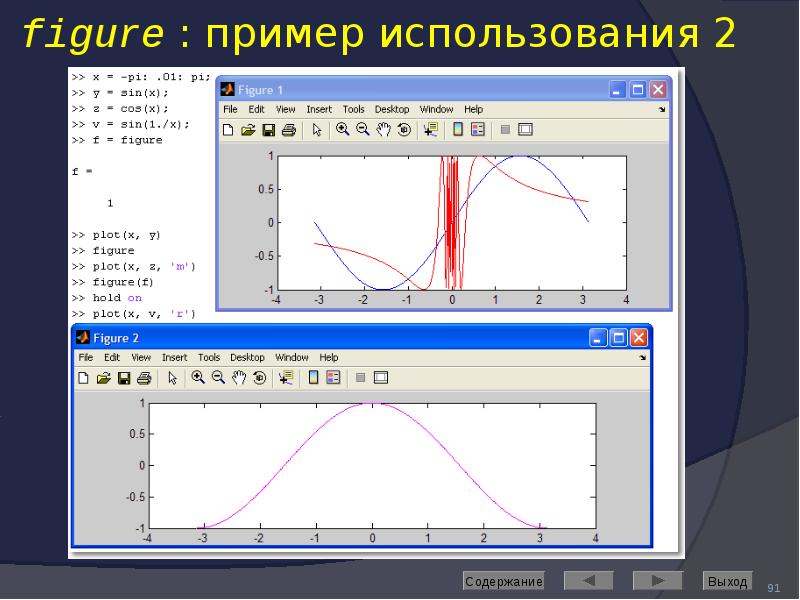
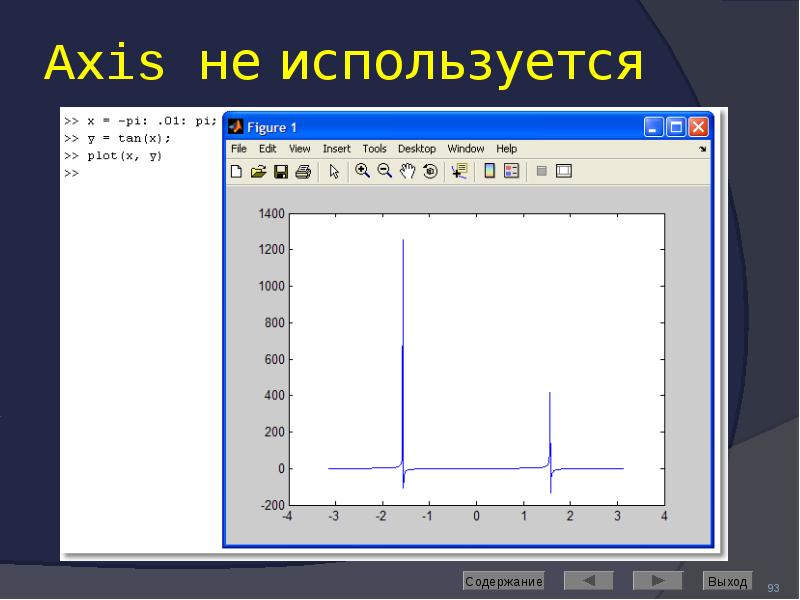
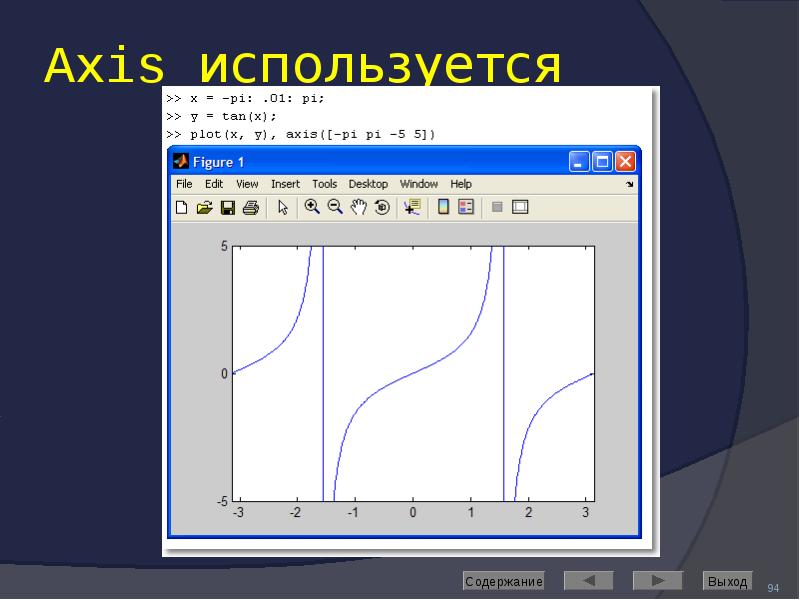
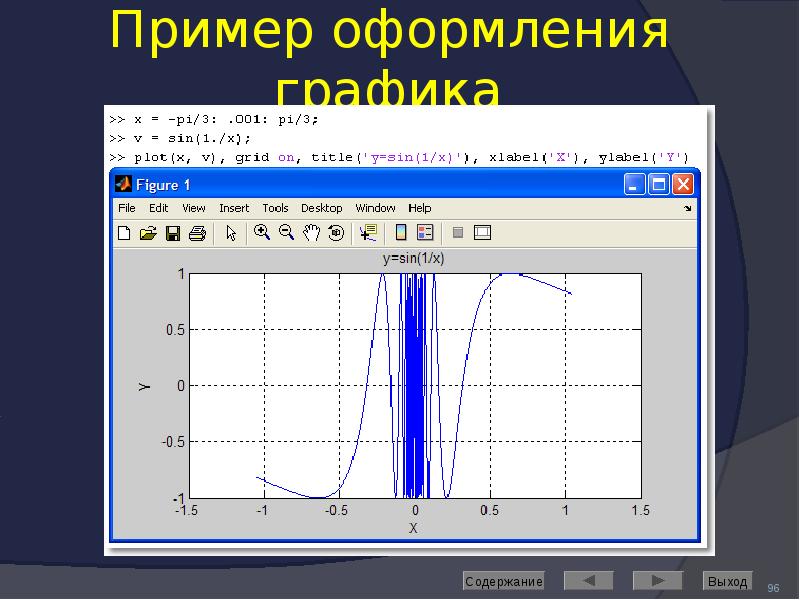
Axis: управление масштабом Команда axis([Xmin Xmax Ymin Ymax]) задаёт область построения графиков по осям X и Y Используется, если результат автомасштабирования неудовлетворителен

Axis не используется

Axis используется

Оформление графиков Для графиков можно задать масштабную сетку: grid on заголовок: title(’заголовок’) подписи осей: xlabel(’текст’) и ylabel (’текст’) В заголовках и подписях можно использовать нотацию системы TeX

Пример оформления графика

Форматирование графиков Доступно из меню Edit:

Графики функций, заданных параметрически Строятся при помощи оператора plot Вначале задаётся диапазон построения t Затем вычисляются x(t) и y(t) И строится график

Графики параметрических функций часто возникают в физических приложениях Графики параметрических функций часто возникают в физических приложениях Независимая переменная t в этом случае имеет смысл времени, x и y – координаты Для построения динамического графика можно использовать функцию comet(x,y)

Функции в полярной СК Строятся аналогично графикам функций в декартовой системе Для построения используется команда polar

Трёхмерная (3D-) графика Построение поверхностей контурных диаграмм (линии равного уровня) 3D-линий векторных полей скалярных полей и др.

Построение 3D-поверхности Рассмотрим пример: построить поверхность f(x,y)=sin(r)/r, где r=sqrt(x2+y2)

Функция meshgrid возвращает две матрицы – X и Y – которые определяют область построения функции Функция meshgrid возвращает две матрицы – X и Y – которые определяют область построения функции Если диапазоны по X и Y разные, то функции передаются два диапазона Собственно поверхность выводится функцией surfl

Функции для построения поверхностей О других графических функциях можно узнать в системе помощи Matlab

ПРОГРАММИРОВАНИЕ В MATLAB

Типы программных файлов Написание программ – это альтернатива работе в командной строке Программный код Matlab размещают в файлах с расширением «m» (m-файлах) m-файлы бывают двух видов: скрипты (scripts) функции (functions)

Скрипты Представляют собой последовательности команд Matlab как если бы мы перенесли их из командного окна в отдельный файл Вызываются по имени через командную строку. Выполняются в режиме построчного анализа, обработки и выполнения исходных команд

Полезны для автоматизации последовательности действий, которые выполняются многократно. Полезны для автоматизации последовательности действий, которые выполняются многократно. Не могут принимать параметры и возвращать аргументы. Хранят значения своих переменных в рабочем пространстве где переменные доступны для других скриптов и из командной строки

Функции Специальный вид m-файлов. В отличие от скриптов могут принимать аргументы и возвращать значения. Использование функций позволяет структурировать программу избежать повторения кода

Создание функции преследует целью расширение языка. Создание функции преследует целью расширение языка. Переменные, определённые внутри функции являются локальными то есть видны только внутри самой функции. Функция имеет собственное имя. Кроме того, с ней связано имя m-файла, в котором функция записана будем соблюдать правило: имя функции и имя m-файла должны быть одинаковы

Структура функции Функция состоит из заголовка и тела function f = fact(n) Заголовок % Вычисляет факториал. Линия H1 % FACT(N) возвращает N!, Help f = prod(1:n); Тело функции H1 и Help выводятся по команде help <имя функции> Фактически, функция отличается от скрипта наличием заголовка и способом вызова

Заголовок функции function f = fact(n)

Комментарии Используются для пояснения кода; временного исключения кода из текста. Могут быть строчными и блочными Строчные начинаются с символа «%» с этого места и до конца строки всё игнорируется компилятором % как в этом примере Блочные начинаются с символа «%{» и заканчиваются символом «%}»: %{ эти символы должны обязательно стоять в отдельных строках! %}

Можно автоматически закомментировать блок текста. Для этого: Можно автоматически закомментировать блок текста. Для этого: выделить блок щёлкнуть правой кнопкой выбрать Comment (или Ctrl+R) Снять комментарий: выделить закомментированный блок щёлкнуть правой кнопкой выбрать Uncomment (или Ctrl+T)

Создание функции m-файл можно создать в любом текстовом редакторе. Например, во встроенном редакторе при помощи меню или командой edit <имя файла>

Использование функции Функция вызывается по своему имени (которое совпадает с именем её m-файла)

Входные и выходные параметры При написании функций в Matlab можно проводить проверку количества входных и выходных параметров. Для этого в описании функции используют служебные слова: nargin: количество входных параметров nargout: количество выходных параметров

Подфункции В файлах-функциях Matlab могут быть реально описаны несколько функций Синтаксически это оформляется как две (или более) функций, записанных в одном файле При вызове такого m-файла происходит запуск самой первой функции её имя должно совпадать с именем файла Описание следующих функций локально обычно они используются как вспомогательные для первой функции

Вложенные функции Помимо последовательного вложения в один файл функция может быть описана непосредственно в теле другой функции Такая функция называется вложенной Вложенная функция, в свою очередь, может содержать другие вложенные функции

Создание p-кода При вызове m-файла сравнительно много времени тратится на его компиляцию Чтобы сократить время выполнения можно предварительно перевести m-файл в p-код («пи-код») команда pcode <имя m-файла> Откомпилированный в псевдокод файл получает расширение «p» Такой файл будет выполняться быстрее, чем обычный m-файл

Интерактивный ввод данных Используется при написании скриптов Для ввода числовых данных применяют функцию input по формату x = input(’строка приглашения’) Введённое пользователем значение сохранится в переменной x Для ввода строковых данных функция input вызывается с дополнительным параметром: c = input(’строка приглашения’,’s’) Кроме того, имеется Си-подобная функция sscanf

Пример использования input

Вывод данных в командное окно Для этого используют команду disp (от display) по формату disp(<выводимая строка>) Если выводимое значение – число, то вначале его преобразуют к строковому типу при помощи функций int2str или num2str Конкатенацию строк производят как для одномерных векторов-строк

Основные языковые конструкции Как и любой процедурный язык высокого уровня, Matlab позволяет использовать при написании программ следование ветвление циклы пользовательские функции

Следование Реализуется перечислением каждого из операторов в отдельной строке Либо в одной строке через запятую (или точку с запятой)

Ветвление Реализуется в двух вариантах: при помощи оператора if при помощи оператора switch

Оператор if Простейшая форма: if <логическое выражение> <операторы> end

Полный формат оператора if В полном варианте оператора могут использоваться слова else и elseif Слово elseif может использоваться в одном операторе многократно с указанием условия Слово else – только один раз в конце оператора и без условия

Циклы В Matlab имеется два вида циклов: цикл с параметром for цикл c предусловием while Также имеются оператор досрочного выхода из цикла break оператор перехода к следующей итерации continue

Цикл с параметром

Замечание по использованию цикла с параметром Обычно цикл for используется для обработки массивов Важно помнить, что если есть возможность обойтись без этого цикла (применить матричные или векторные операции), то лучше избавиться от явного цикла В этом случае программа будет работать на порядок быстрее

Пример: замена отрицательных элементов вектора на нули (с циклом)

Пример: замена отрицательных элементов вектора на нули (без цикла)

Цикл с предусловием Синтаксис: while <логическое выражение> <операторы> end Операторы выполняются, пока логическое выражение есть истина (true)

Операторы break и continue Аналогичны одноимённым операторам Паскаля Break производит досрочный выход из цикла for или while Continue прекращает выполнение текущей итерации и переходит к следующей

Операторы break и continue (пример) Написать скрипт, который вводит с клавиатуры произвольное количество чисел. Если число положительное, то оно прибавляется к сумме, если отрицательное, то пропускается. Ноль – признак окончания работы

Операторы break и continue (решение)

АНАЛИТИЧЕСКИЕ ВЫЧИСЛЕНИЯ В MATLAB

Вычисления в Matlab Пример: вычисление определённого интеграла По формуле Ньютона: F(x)|ab =F(b) – F(a), где F(x) – первообразная получаем точный результат но первообразную не всегда можно найти Численно: методом прямоугольников, трапеций, Симпсона и пр. можно пользоваться даже тогда, когда интеграл «не берётся» но при вычислении возникают погрешности

Средства Matlab для символьных вычислений Изначально Matlab имел средства только для численного анализа Сегодня в Matlab встроены средства аналитических (символьных) вычислений Symbolic Math Toolbox Является вычислительным ядром системы Maple V Установка Maple не требуется

Создание символьных переменных Для символьного анализа требуется создать символьные переменные и функции Символьные переменные создаются по одной: x=sym(’x’) так же можно создать целое символьное выражение несколько сразу: syms x y z Символьные функции определяются через символьные переменные: f=x^2+y Для построения символьных функций можно воспользоваться командой ezplot Представить в стандартной форме – командой pretty

Представление символьных переменных

Символьные вычисления Преобразования математического анализа дифференцирование, пределы, интегрирование, разложение в ряд Тейлора Упрощение и подстановки Точная арифметика Линейная алгебра Решение уравнений и их систем обычных и дифференциальных

Дифференцирование

Частные производные

Пределы

Односторонние пределы Рассмотрим функцию f(x)=x/|x|

Пределы (сводная таблица)

Интегралы

Интегралы с параметрами

Суммирование

Разложение в ряд Тейлора

Пример: исследование функции

Найдём горизонтальную асимптоту

Найдём вертикальные асимптоты

Код для построения асимптот

Изображение асимптот

Экстремумы функции

Построение экстремумов

Операции над полиномами Реализуются при помощи функций collect expand factor horner

collect – вычисляет коэффициенты при степенях независимой переменной collect – вычисляет коэффициенты при степенях независимой переменной по умолчанию – x Можно явно задать имя независимой переменной в виде: collect (f, VarName)

expand – представляет полином суммой степеней без приведения подобных expand – представляет полином суммой степеней без приведения подобных

factor – разлагает полином на множители, если эти множители имеют рациональные коэффициенты: factor – разлагает полином на множители, если эти множители имеют рациональные коэффициенты:

Также factor производит каноническое разложение числа: Также factor производит каноническое разложение числа:

horner – представляет полином в схеме Горнера: horner – представляет полином в схеме Горнера:

Упрощение выражений simplify реализует мощный алгоритм упрощения с использованием тригонометрических, степенных, логарифмических, экспоненциальных функций, а также спецфункций (Бесселя, гипергеометрической, интеграла ошибок и пр.) simple пытается получить выражение, которое представляется меньшим числом символов, чем исходное, последовательно применяя все функции упрощения Symbolic Math Toolbox

Simplify

Simple

Simplify против Simple Иногда simple даёт более удачное решение, чем simplify:

Simple simple особенно эффективна при работе с тригонометрическими выражениями

Подстановка subs подставляет одно символьное выражение в другое Общий формат: subs(<куда>, <вместо чего>, <что>)

Пример подстановки

Подстановка значения в функцию Подстановка вместо переменной её числового значения приводит к вычислению символьной функции от значения аргумента

Точная арифметика Точные вычисления реализуются функцией vpa (Variable-Precision Arithmetic) Формат вызова: vpa(<выражение>, <значащих цифр>)

Решение уравнений и систем Выполняет команда solve До 4-го порядка включительно решаются точно Ответ выводится в степенях рациональных чисел Уравнения высших порядков и трансцендентные, как правило, точно не решаются В этом случае выводится приближённый результат С целью сокращения записи при выводе могут использоваться подстановки

Решение систем Также выполняет команда solve Входные аргументы левые части уравнений переменные, по которым нужно разрешить систему например: s = solve(f1, f2, x1, x2) Выходной аргумент структура (запись) s с полями (в данном случае) x1 и x2, хранящими символьное представление решения

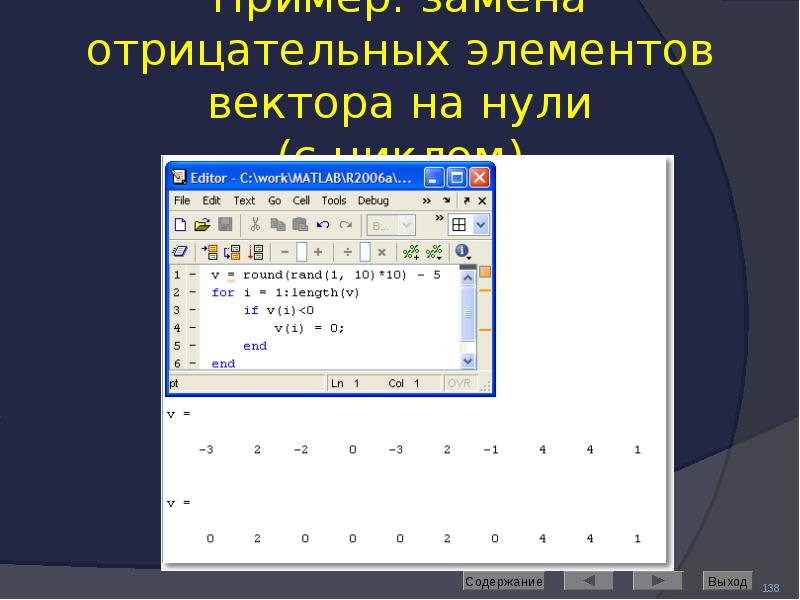
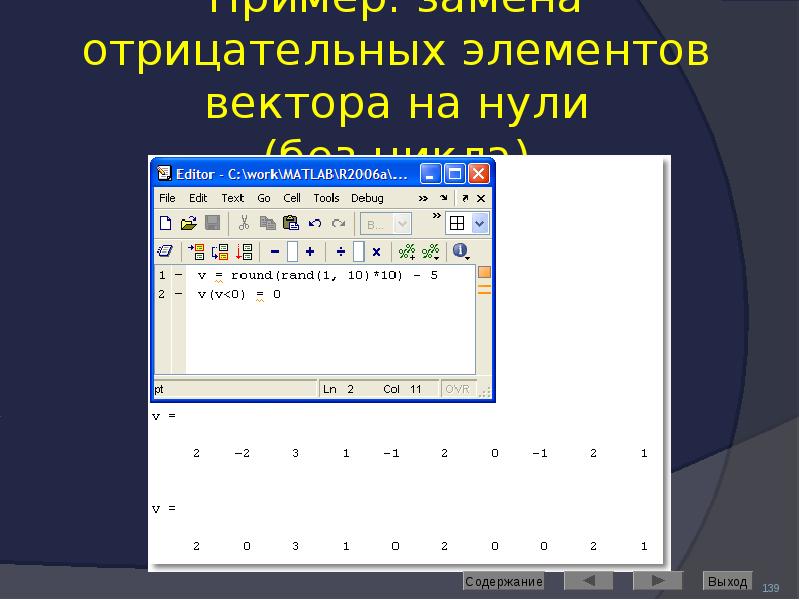
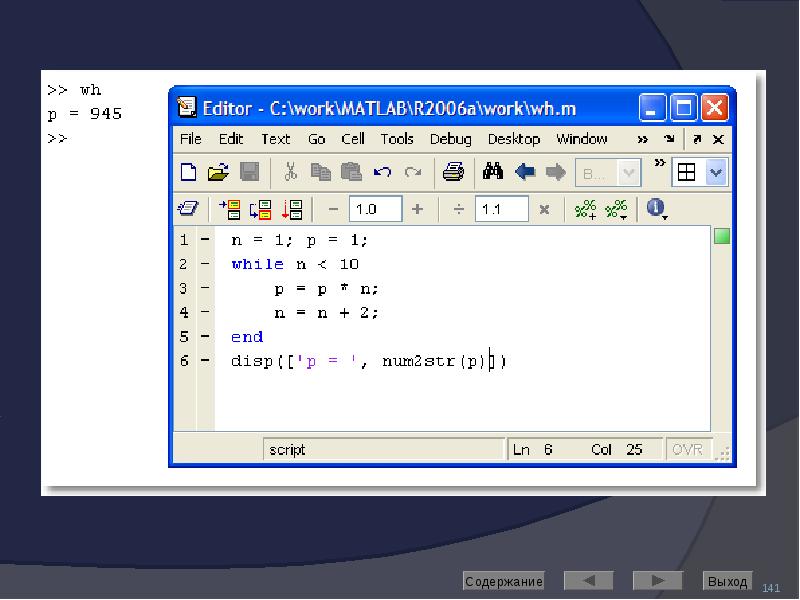
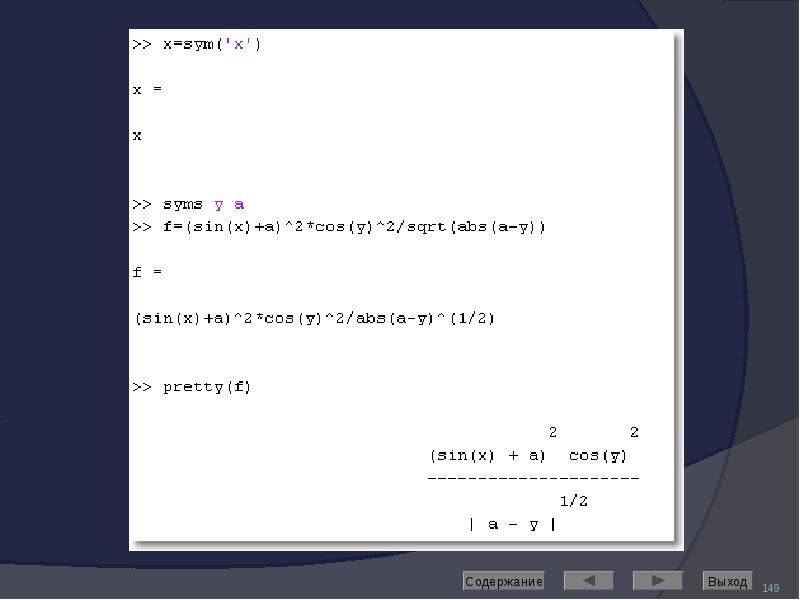
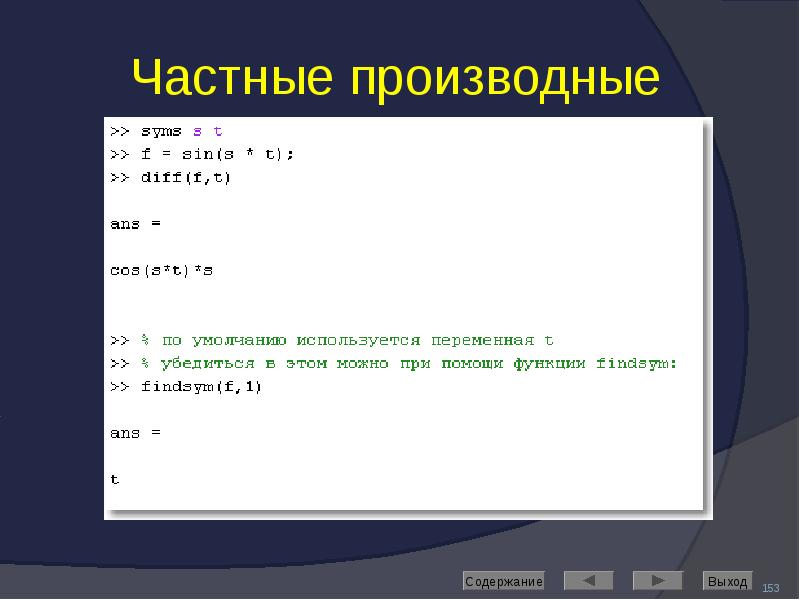
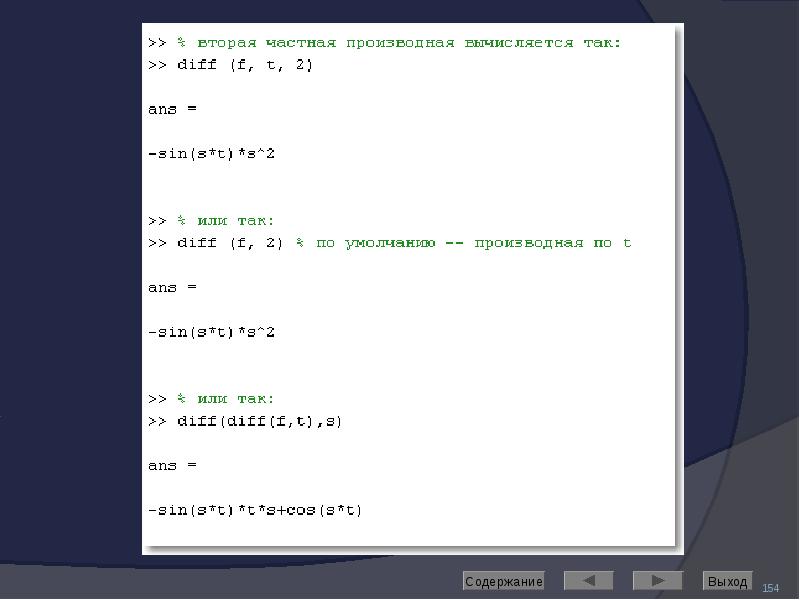
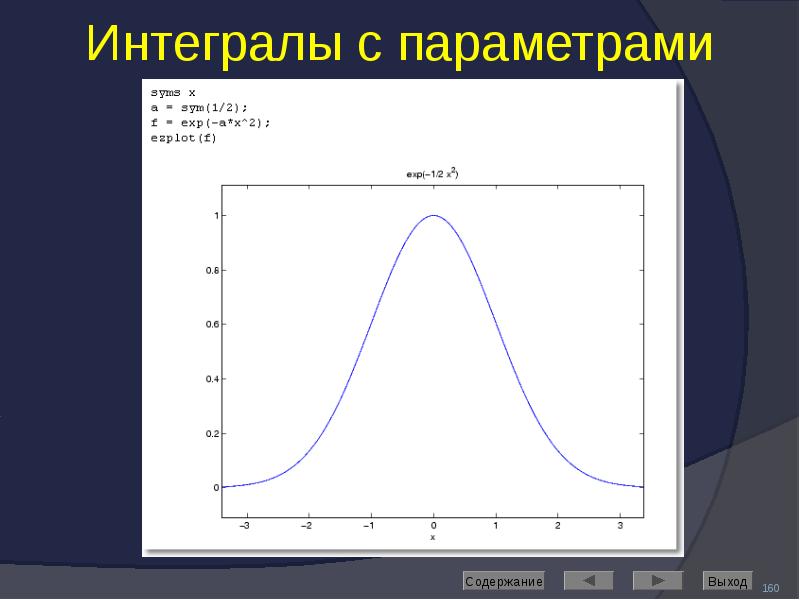
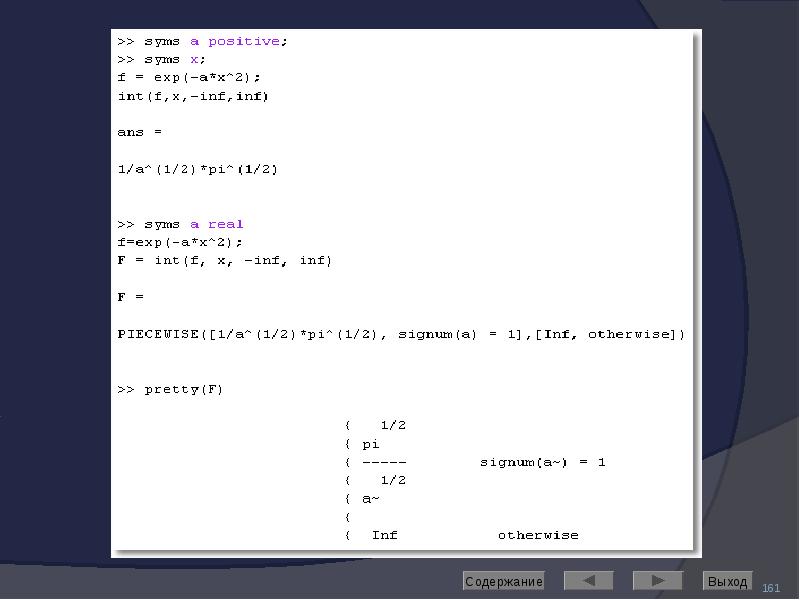
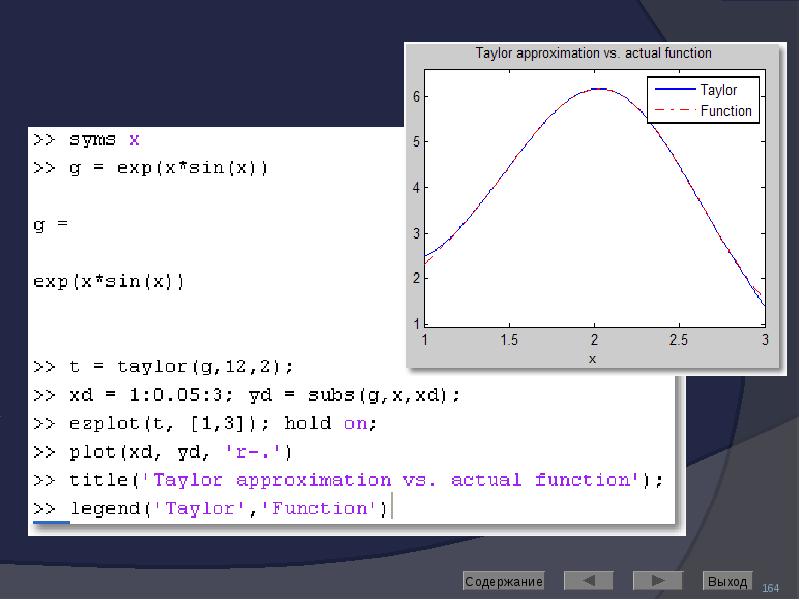
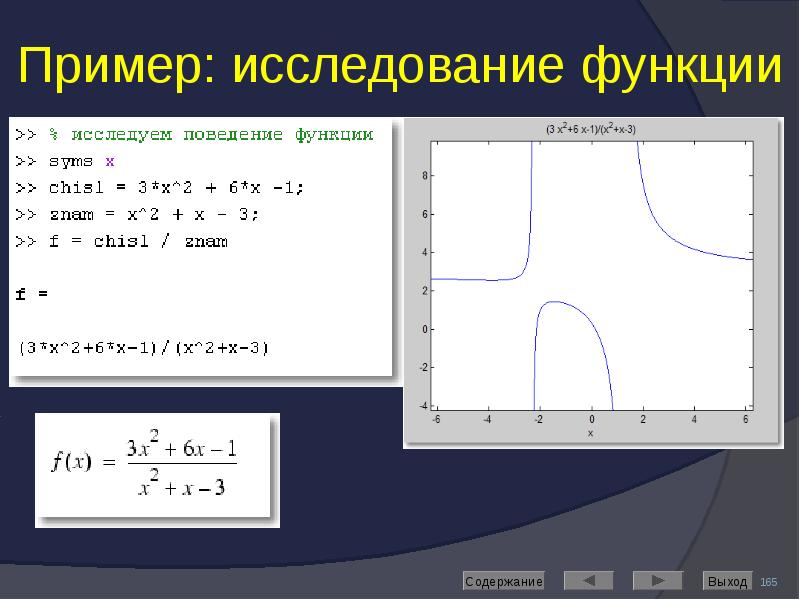
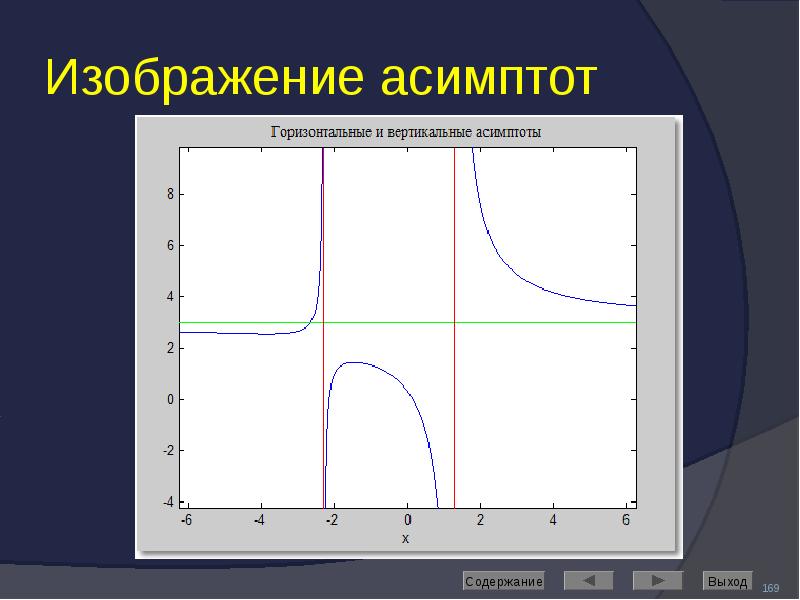
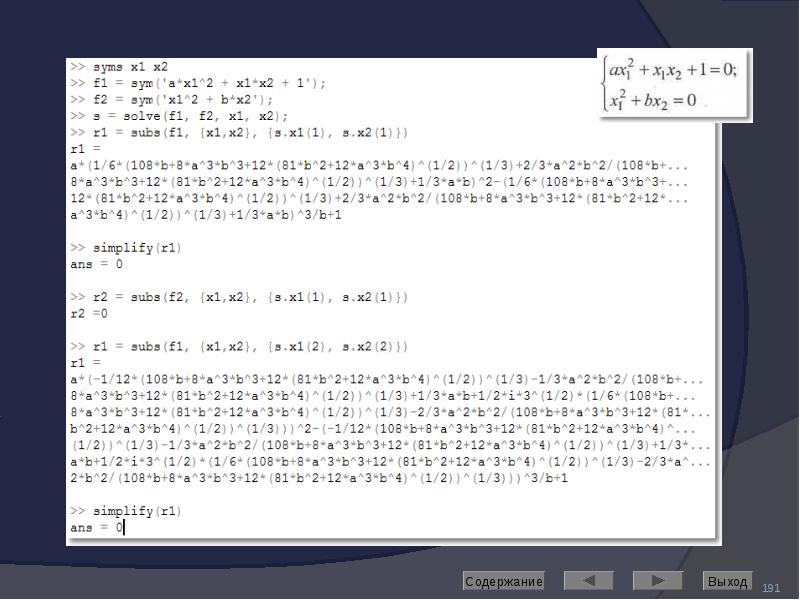
Решение дифференциальных уравнений Выполняет команда dsolve Если неизвестная функция обозначена символьной переменной y, то ее производные следует обозначать как d[n]y, где в скобках указан порядок производной.

MATLAB В ЗАДАЧАХ ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (ТАУ)

Представление и преобразование математических моделей (ММ) динамических систем (ДС). Представление и преобразование математических моделей (ММ) динамических систем (ДС). Задание ДС в матрично-векторной (МВ) форме записи В современной теории управления для описания ММ ДС используется запись, представляющая собой систему уравнений в переменных состояния [1] (1)

Задание ДС во вход-выходной (ВВ) форме записи Задание ДС во вход-выходной (ВВ) форме записи В классической теории управления для описания ММ ДС используется понятие передаточных функций (ПФ), которые представляют собой дробно-рациональную функцию [2] (2) Для ввода ПФ коэффициенты числителя и знаменателя необходимо задавать в виде вектора (в порядке убывания степени). NUM=[bm bm-1 ... b1 b0] DEN=[am am-1 ... a1 a0]

Анализ математических моделей динамических систем Анализ математических моделей динамических систем

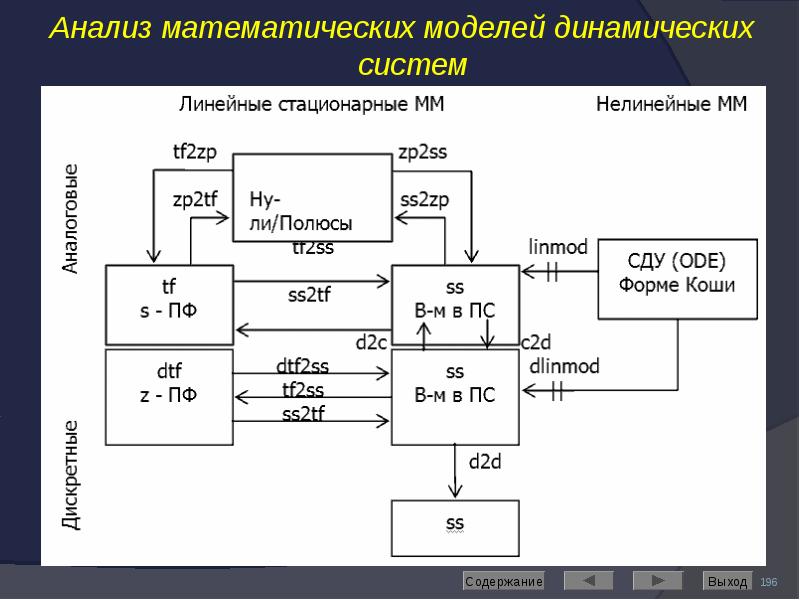
Преобразование ПФ: Преобразование ПФ: [NUMc,DENc]=tfchk(NUM,DEN) – проверяет на соответствие порядки числителя и знаменателя, возвращает эквивалентную ПФ с равными порядками (отсутствующие коэффициенты заполняются нулями) или выдает сообщение об ошибке; [Z,P,K]=tf2zp(NUM,DEM) – находит нули, полюсы и коэффициент передачи (приведенный); [NUM,DEN]=zp2tf(Z,P,K) – обратное преобразование; [A,B,C,D]=tf2ss(NUM,DEN) – преобразуем ПФ с одним входом в модель ПС в канонической форме управления. Для перехода также все матрицы необходимо развернуть на 1800: A=rot90(A,2), B=rot90(B,2) и т.д.; abcdchk(A,B,C,D) – проверяет согласованность размерности матриц и в случае ошибки возвращает сообщение о ней; [Wn,ksi]=damp(A) – вычисляет сопрягающие частоты и коэффициенты затухания ДС (А может быть либо системной матрицей, либо векторами NUM или DEN, либо векторами корней Z или P);

Построение частотных характеристик: Построение частотных характеристик: [Mod,Fi]=bode(A,B,C,D,ui,w), [Mod,Fi]=bode(NUM,DEN,w) – возвращает вектор амплитуды и фазы (ui номер входа в МВ ММ). Для построения ЛЧХ вектор w должен в логарифмическом масштабе содержать значения частот в рад/с. Построение фазовой частотной характеристики для неминимально-фазовых звеньев выше 1-го порядка с использованием данной функции выполняется неправильно. Для коррекции фазовой характеристики имеются следующие характеристики: Fik=fixphase(Fi) или Fik=add360(Fi) – устраняет разрыв фазы от –1800 к 1800. Фаза Fi задается в градусах; Fik=addtwopi(Fi) – то же для фазы, заданной в радианах.

Вычисление переходных процессов: Вычисление переходных процессов: Y – вектор переходного процесса, t – вектор изменения времени, X – вектор состояния (необязательный параметр, может быть опущен) [Y,X]=impulse(A,B,C,D,ui,t), Y=impulse(NUM,DEN,t) – весовая функция, [Y,X]=step(A,B,C,D,ui,t), Y=step(NUM,DEN,t) – реакция на единичное ступенчатое воздействие, [Y,X]=lsim(A,B,C,D,U,t,X0), Y=lsim(NUM,DEN,U,t) – реакция на произвольно заданное вектором U внешним воздействием (X0 – начальное условие).

Анализ управляемости: Анализ управляемости: Q=ctrb(A,B) – вычисляет матрицу управляемости Q, [Ab,Bb,Cb,T]=ctrbf(A,B,C,TOL) – выделение полностью управляемого подпространства, для частично управляемой системы. (TOL – допуск, необязательный параметр, T – матрица преобразования, Ab=TAT-1, Bb=TB, Cb=CT-1). Индекс nc – неуправляемая часть, с – управляемая. Выделение неуправляемой части: nc=length(Ab)-rang(Q); Anc=Ab(1:nc,1:nc). eig(Anc) - cобственные значения неуправляемой части системы.

Анализ наблюдаемости: Анализ наблюдаемости: R=obsv(A,C) – вычисляет матрицу наблюдаемости R, [Ab,Bb,Cb,T]=obsvf(A,B,C,TOL) – выделение полностью наблюдаемого подпространства, для частично наблюдаемой системы. (TOL – допуск, необязательный параметр, T – матрица преобразования, Ab=TAT-1, Bb=TB, Cb=CT-1). Индекс no – ненаблюдаемая часть, о – наблюдаемая. Выделение ненаблюдаемой части: nо=length(Ab)-rang(R); Ano=Ab(1:no,1:no). eig(Ano) - cобственные значения ненаблюдаемой части системы.

Построение графиков: Построение графиков: plot(X,Y,S) – построение графика функции Y(X) c заданием типа линии с помощью S (необязательный параметр); plot3(X,Y,Z,S) – построение трехмерного графика функции Z(X,Y) c заданием типа линии с помощью S (необязательный параметр); loglog(X,Y,S) – аналогична предыдущей команде, но для задания логарифмического масштаба по X и Y; semilogx(X,Y,S) или semilogy(X,Y,S) – строит график в логарифмическом масштабе по оси X или Y соответственно; subplot(m,n,k) – разбивает окно на m окон по горизонтали и n окон по вертикали, а k – номер окна, в котором будет выводиться текущий график;