ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр

Нажмите для полного просмотра!

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №2

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №3

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №4

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №5

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №6

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №7

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №8

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №9

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №10

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №11

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №12

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №13

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №14

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №15

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр, слайд №16

Содержание ▲

Вы можете ознакомиться и скачать презентацию на тему ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их пр. Доклад-сообщение содержит 16 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

Слайд 1

Описание слайда:

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ Кафедра Информационных технологий и управляющих систем Предмет «Вычислительные методы и их применение в ЭВМ» Лекция Доцент Стрельцова Г. А.

Слайд 2

Описание слайда:

Введение Если зависимость y(x) представлена рядом табличных отсчетов yi(xi), то интерполяция значений y(x) – это вычисление значений y(x) при заданном x, расположенном в интервале между отсчетами. За пределами общего интервала определения y(x) , вычисление y(x) называют экстраполяцией (предсказанием значений функции). Аппроксимация в системах компьютерной математики – это получение приближенных значений какого - либо выражения.

Слайд 3

Описание слайда:

Повестка дня Список изучаемых разделов: Интерполяция и ее виды. Особенности аппроксимации функций. Методы интерполяции и аппроксимации. Примеры решения задач интерполяции и аппроксимации в Maple Время, отводимое на каждый раздел: 5-10 минут.

Слайд 4

Описание слайда:

Обзор Разделы лекции

Слайд 5

Описание слайда:

Словарь терминов Интерполирующая функция – это функция F(x), которая принадлежит известному классу и принимает в узлах интерполяции те же значения, что и искомая y(x). Узлы интерполяции y(x)– это значения x в интервале [a, b] определения данной функции y(x), которые однозначно определены.

Слайд 6

Описание слайда:

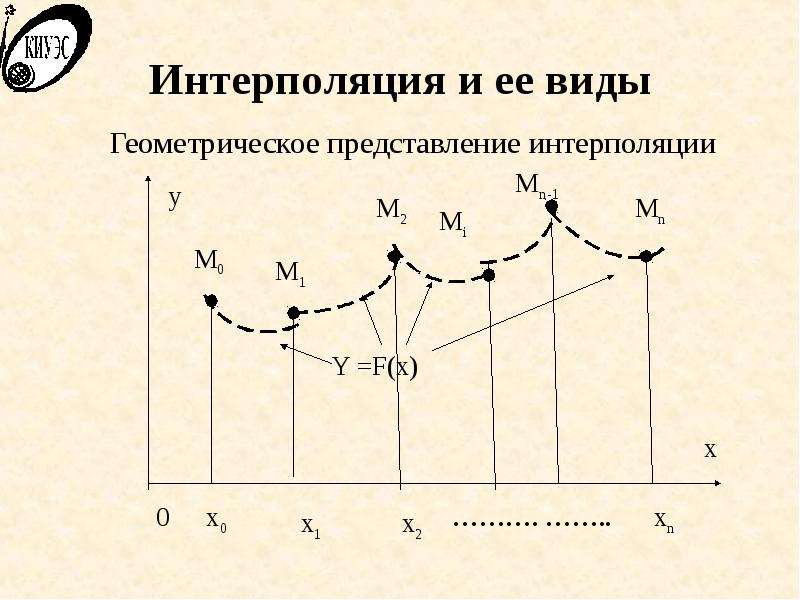
Интерполяция и ее виды Основная задача интерполирования. На отрезке [a, b] заданы n+1 точки x0, x1, … xi, … xn (узлы интерполяции) и значения функции y(x) в этих точках y(x0) = y0, y(x1) = y1, … y(xi) = yi, … y(xn) = yn . Требуется определить интерполирующую функцию F(x), которая: Относится к известному классу, Принимает в узлах интерполяции те же значения, что и y(x): F(x0) = y0, F(x1) = y1, … F(xi) = yi, … F(xn) = yn .

Слайд 7

Описание слайда:

Интерполяция и ее виды Геометрическое представление: Найти кривую y = F(x) определенного типа, проходящую через заданную систему точек M(xi, yi), где I =0,1,2,..n. В общем случае задача является неопределенной. Однако она становится однозначной, если вместо произвольной функции F(x) искать, например, полином Pn(x) степени, удовлетворяющий условиям Pn (x0) = y0, Pn(x1) = y1, … Pn (xi) = yi, … Pn (xn) = yn .

Слайд 8

Описание слайда:

Интерполяция и ее виды Геометрическое представление интерполяции

Слайд 9

Описание слайда:

Интерполяция и ее виды Основные виды интерполяционных полиномов: Канонический полином, Полином Ньютона, Полином Лангранжа, Полином Эйткена, Полином Чебышева.

Слайд 10

Описание слайда:

Особенности аппроксимации функций Под аппроксимацией функциональных зависимостей подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, которая дает точное значение искомой функции y(x) в узловых точках в пределах погрешности вычислений по умолчанию. Для этого также используют степенные многочлены - полиномы или линейные функции.

Слайд 11

Описание слайда:

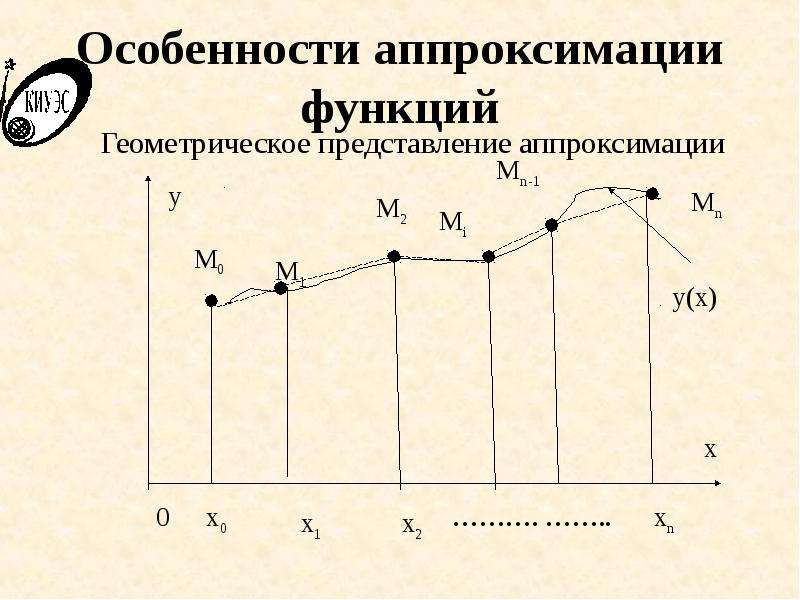
Особенности аппроксимации функций Геометрическое представление аппроксимации

Слайд 12

Описание слайда:

Методы интерполяции и аппроксимации Полиномиальные Сплайновые Линейные Рациональные (отношение двух полиномов) Метод наименьших квадратов Тригонометрические (рядами Фурье).

Слайд 13

Описание слайда:

Примеры решений задач интерполяции и аппроксимации в Maple Пример. Найти приближенное значение функции z(t) при заданном значении аргумента в табличной форме в точках x = 1, 1.5, 2. построить график найденной зависимости y(x). Решение. >t:=[данные из таблицы]; >z:=[данные из таблицы]; >x;=[1, 1.5, 2.0]; >interp(t,z,x);

Слайд 14

Описание слайда:

Примеры решений задач интерполяции и аппроксимации в Maple >z:=y→interp(t,z,x); >for i from 1 to 3 do x[i]:=z(x[i]); end do; >l:=[[t[n], z[n] Sn=1..9]; > plot(l,z(y)], y=0.66..3.12,style=[point, line], symbol=circle) Задача сплайн-интерполяции Используется функция spline(X, Y, x, method), где параметр method определяет вид сплайна. В качестве данного параметра используются ключевые слова linear, quadratic, cubic, quadric или числа 1,2 3, 4. Если параметр не указан, то используется кубический сплайн.

Слайд 15

Описание слайда:

Примеры решений задач интерполяции и аппроксимации в Maple Решение : > spline(t, z, y); > zs:=y → spline(t, z, y); > for I from 1 to 3 do xs[i]:=zs(x[i]); end do; ZSL:=y → spline(t, z, y, l); > l:=[[t[n], z[n] Sn=1..9]; > plot(l, zs(y), zsl(y)], y=0.66..3.12, style [point, line, line], symbol=circle)