🗊Презентация Класс элементарных функций и их графики

Научно-исследовательская работа по теме «Класс элементарных функций и их графики» Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ. Руководитель Крючкова Татьяна Борисовна учитель, математики.

Оглавление: Оглавление 1. Введение. 2.Из истории развития функции 3. Способы задания функции 4. Класс элементарных функций. 4.1.Основные элементарные функции. 4.2. Построение графиков 5. Преобразование исходного графика функции y=f(x). 6. Заключение 7.Список литературы

Введение. Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Как образно заметил великий Галилео Галилей (1564 – 1642 гг.), книга природы написана на математическом языке, и ее буквы – математические знаки и геометрические фигуры, без них невозможно понять ее слова, без них тщетно блуждание в бесконечном лабиринте. И именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения, присущие природе. Изучая квадратичную функцию в 9 классе, мы выполняли преобразования графика этой функции. В результате этих преобразований построение графика выполнялось легко и просто. И я задумался: «А нельзя ли выполнять аналогичные преобразования с графиками других функций, например линейной функции, обратной пропорциональности, степенной функции?». Поэтому я выбрал тему своей работы «Класс элементарных функций и их графики», поставив перед собой цель: понять и изучить способы образования элементарных функций и преобразования их графиков.

Из истории развития функции. Впервые функция вошла в математику под именем «переменная величина» в знаменитом труде французского математика и философа Р. Декарта «Геометрия», и её появление послужило, по словам Ф. Энгельса, поворотным пунктом в математике, благодаря чему в неё вошли движение, диалектика. Без переменных величин И.Ньютон не смог бы выразить законы динамики, описывающие процессы механического движение тел – небесных и вполне земных, а современные ученые не могли бы рассчитывать траектории движения космических кораблей и решать бесконечное множество технических проблем нашей эпохи.

Из истории развития функции. С развитием науки понятие функции уточнялось и обобщалось. Сейчас оно стало настолько общим, что совпадает с понятием соответствия. Таким образом, функцией в общем понимании называется любой закон (правило), по которому каждому объекту из некоторого класса, области определения функции, поставлен в соответствие некоторый объект из другого (или того же) класса – области возможных значений функции. Но мы не рассматриваем понятие функции в столь общем понимании, а считаем, что как независимая, так и зависимая переменные – это величины. Таким образом функцией называется зависимость, связывающая с каждым значением одной переменной величины (аргумента) из некоторой области ее изменения определенное значение другой величины (функции). Если аргумент обозначить через х, значение функции - через у, а саму зависимость – функцию – символом f, то связь между значениями функции и аргументом так: y=f(x).

Способы задания функций. Существуют три основных способа выражения зависимостей между величинами: табличный, графический и аналитический («формульный»). Табличный способ важен потому, что является основным при обнаружении реальных зависимостей и может оказаться к томуже единственным средством их задания (формулу не всегда удается подобрать, а порой в ней и нет необходимости).К табличному заданию функции часто переходят при выполнении практических расчетов, с ней связанных: например, применение таблиц квадратных корней удобно при проведении расчетов, в которых участвуют такие корни. С математической точке зрения, табличное задание непрерывных зависимостей всегда неполно и дает лишь информацию о значениях функции в отдельных точках.

Способы задания функций Графический способ представления зависимостей также является одним из средств их фиксации при изучении реальных явлений. Это позволяет делать различные «самопишущие» приборы, такие, как сейсмограф, электрокардиограф, осциллограф и т.п., изображающие информацию об изменении измеряемых величин в виде графиков. Но если есть график, то значит, определена и соответствующая ему функция. В таких случаях говорят о графическом задании функции. Однако графический способ задания функции неудобен для расчетов; к тому же, подобно табличному, он является приближенным и неполным. Аналитическое (формульное) задание функции отличается своей компактностью, легко запоминается и содержит в себе полную информацию о зависимости. Функцию можно задать с помощью формулы, например: y=2x+5, S=at2/2, S=vt. Эти формулы можно вывести с помощью геометрических или физических рассуждений. Порой формулы получаются в результате обработки эксперимента, такие формулы называются эмпирическими.

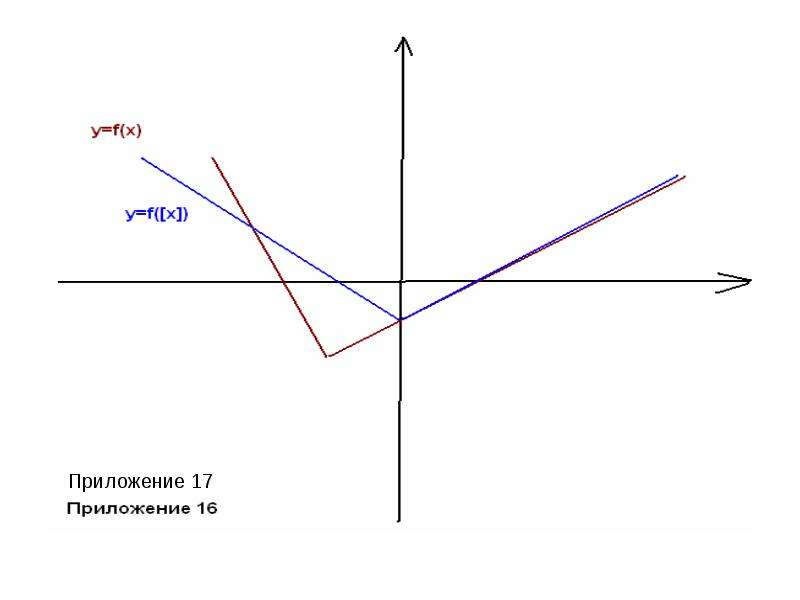
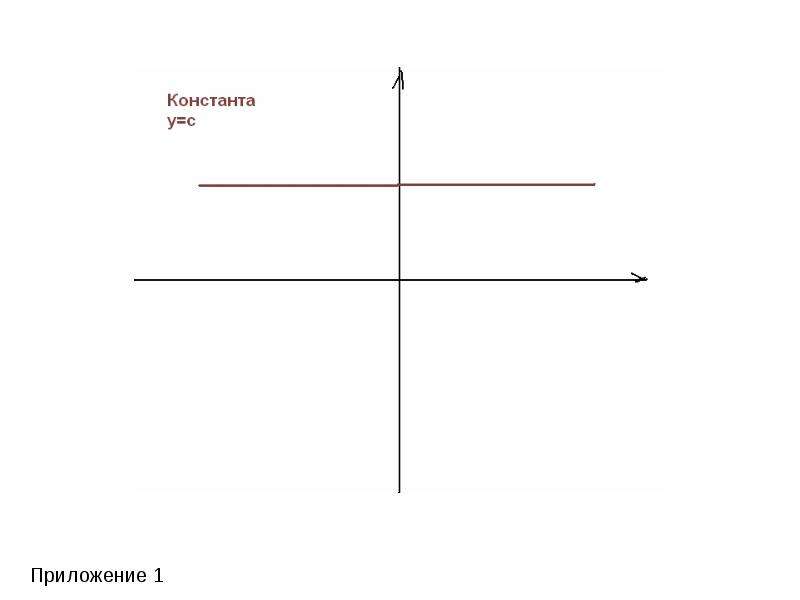
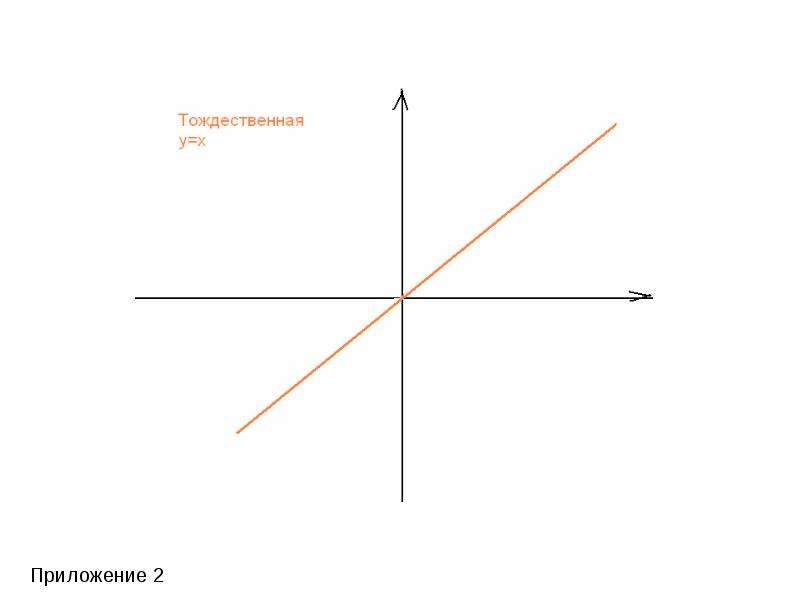
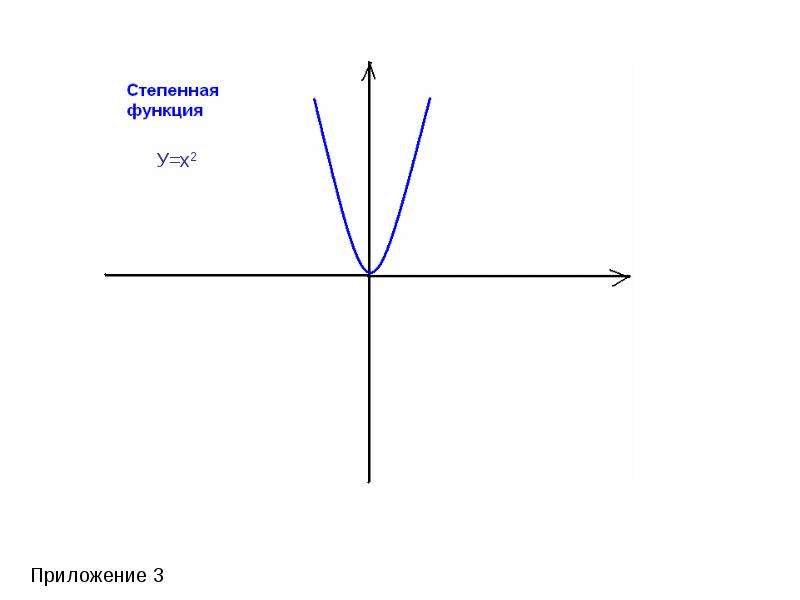
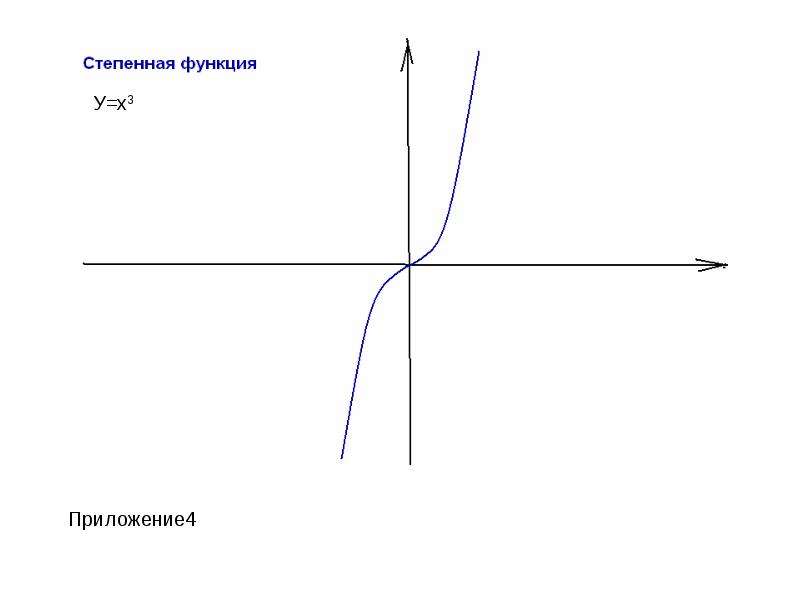
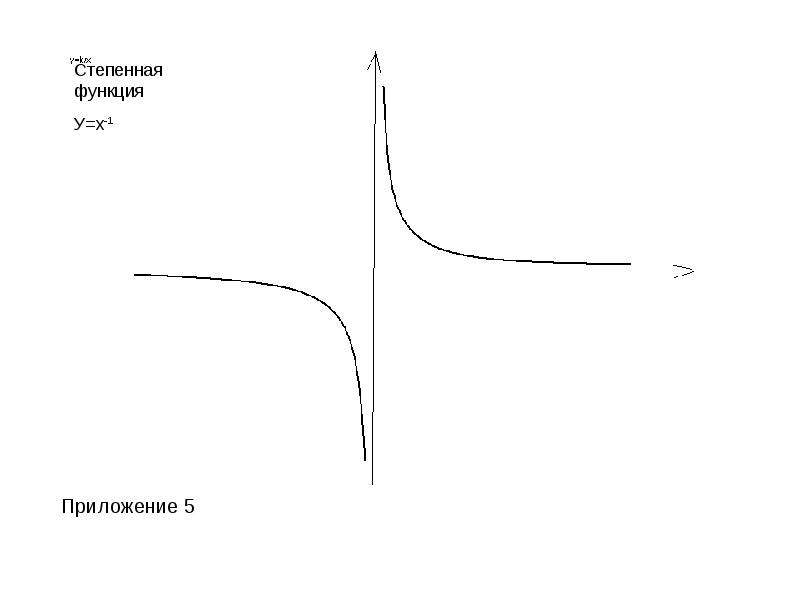
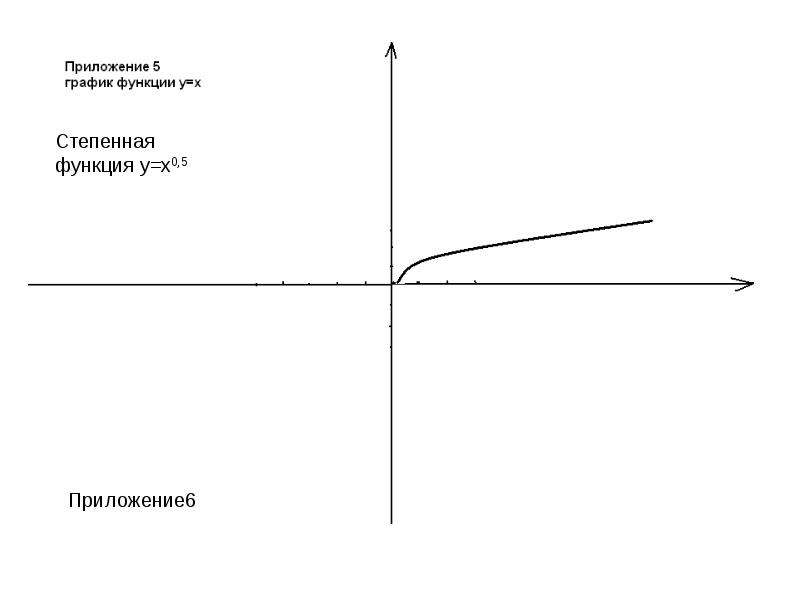
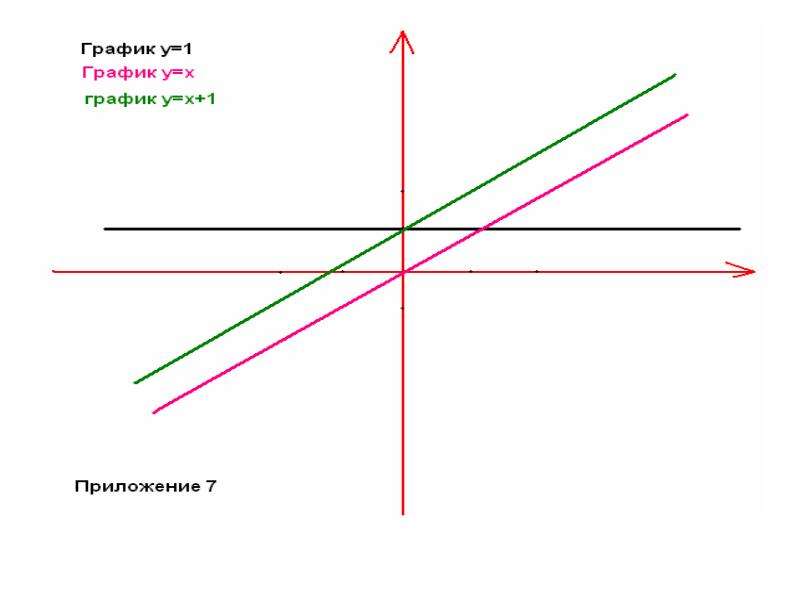
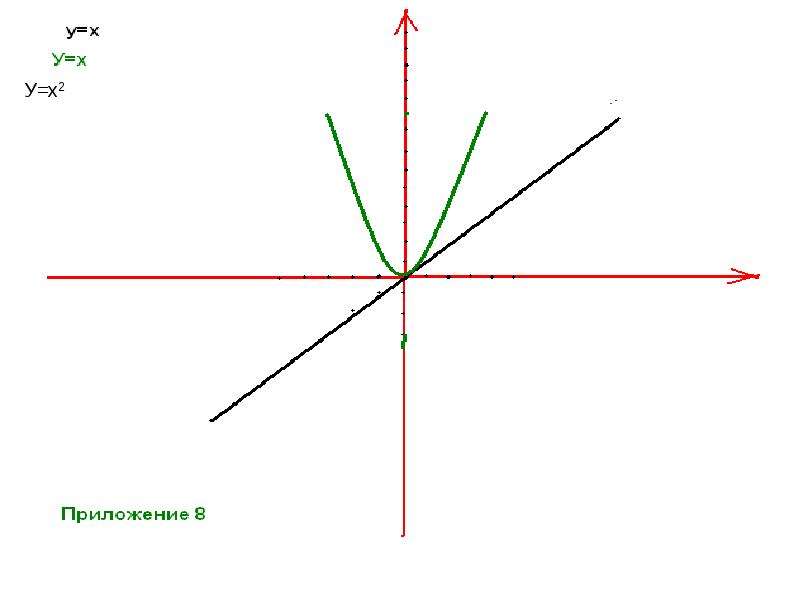
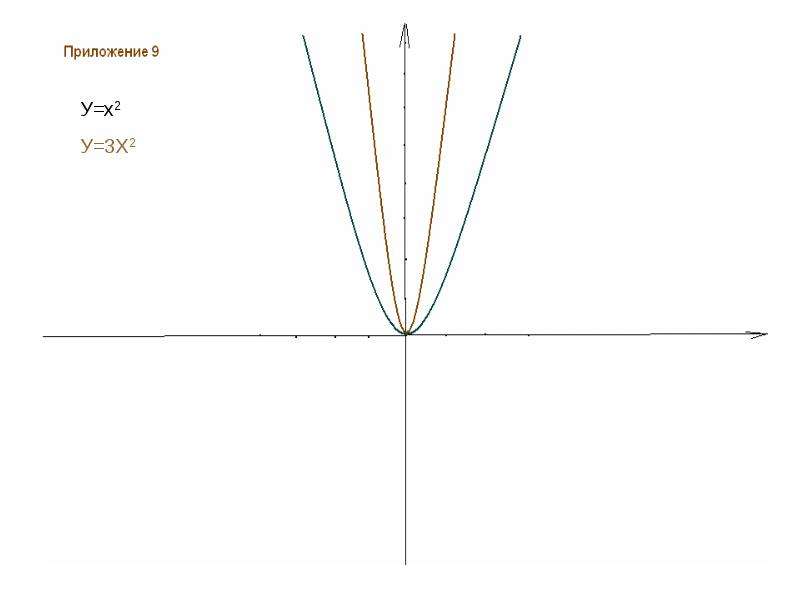
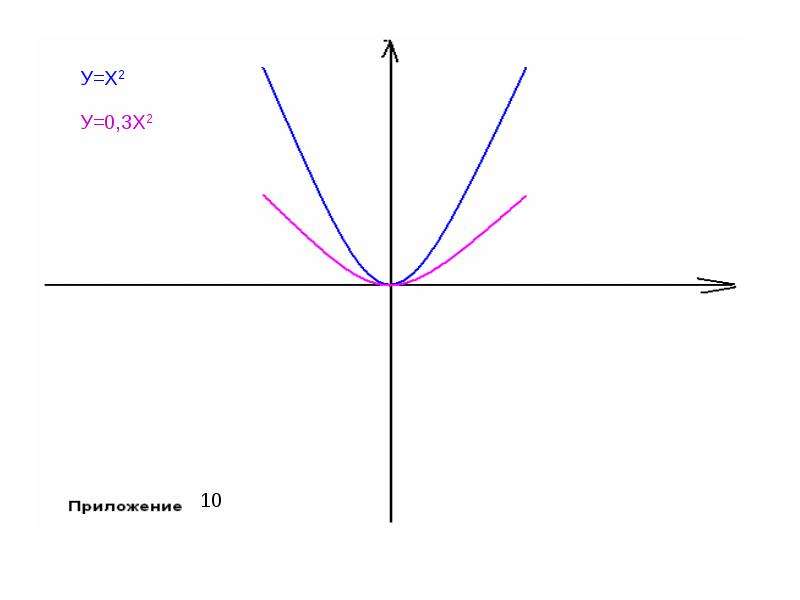
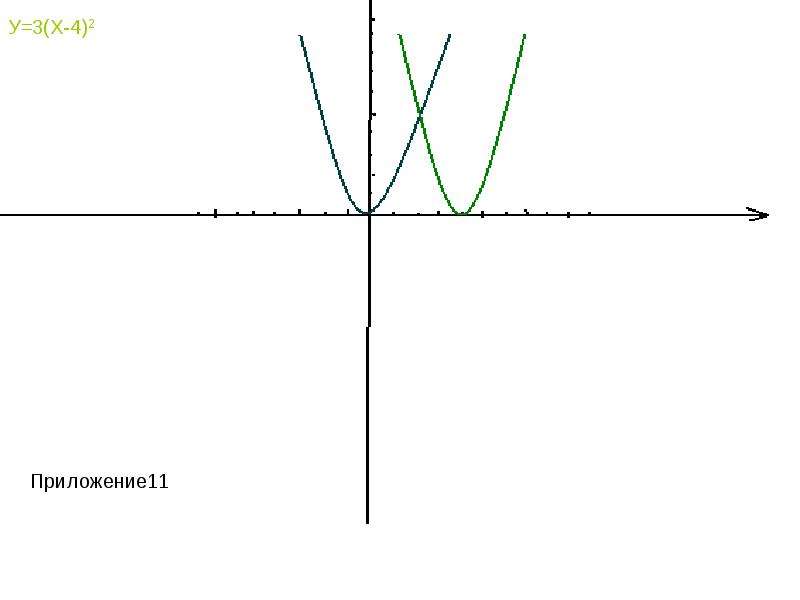
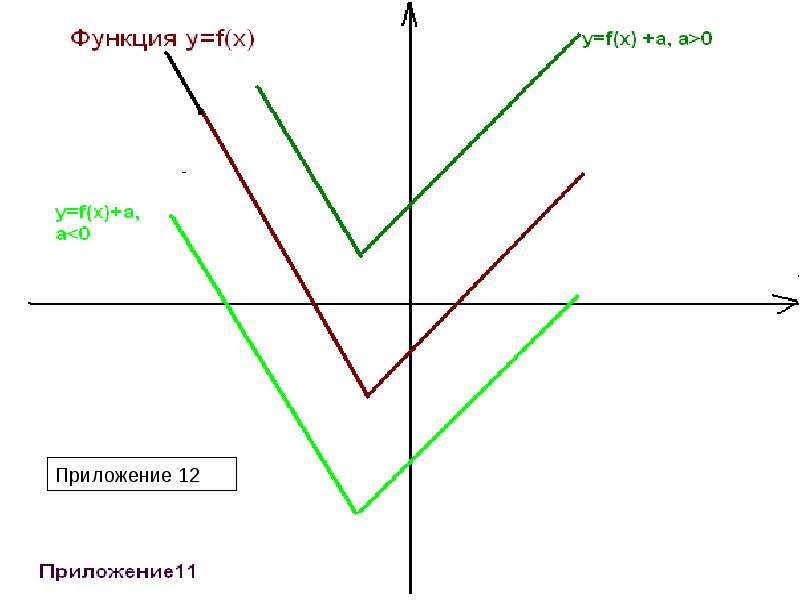
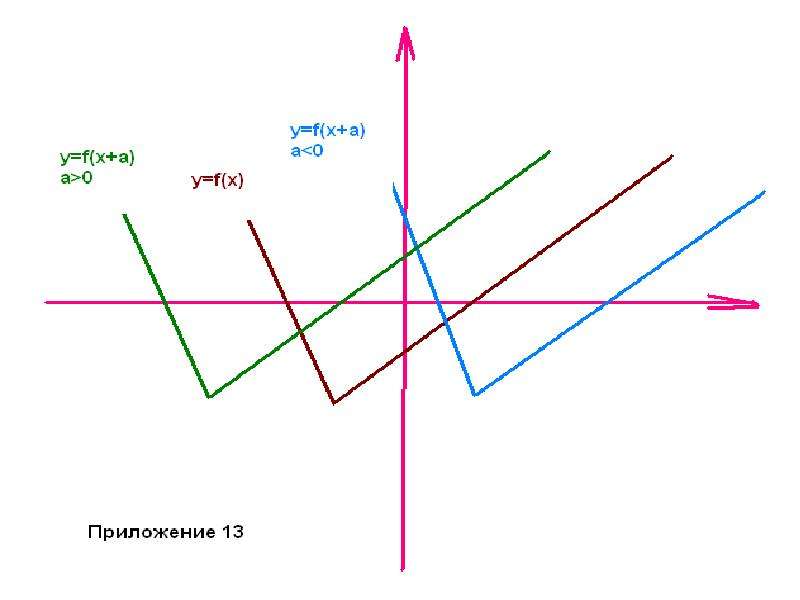
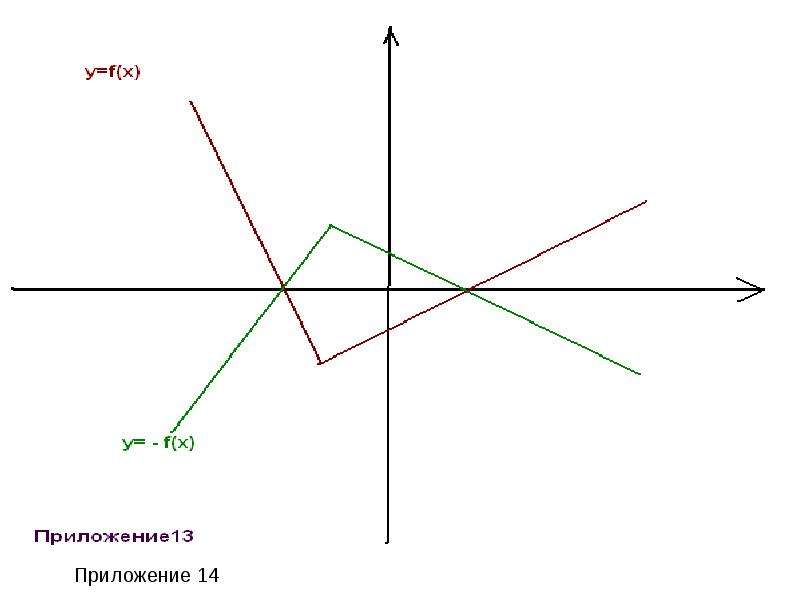
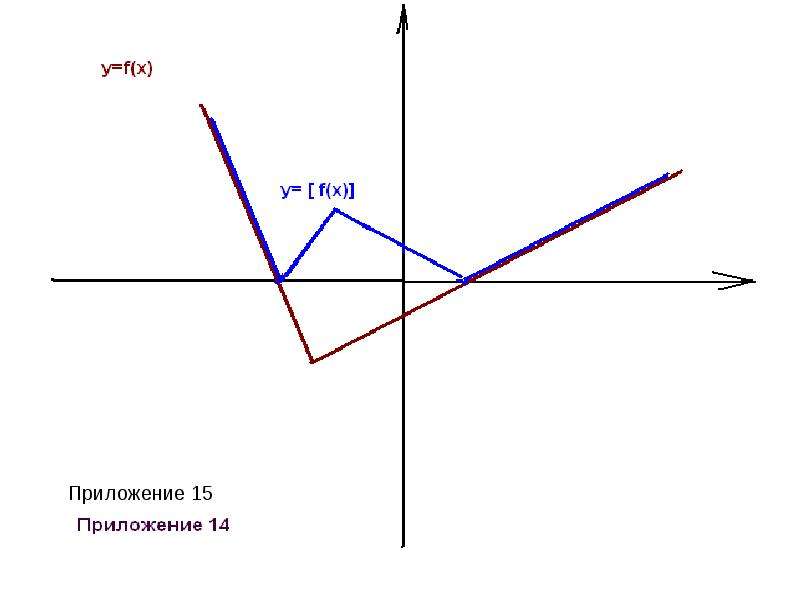
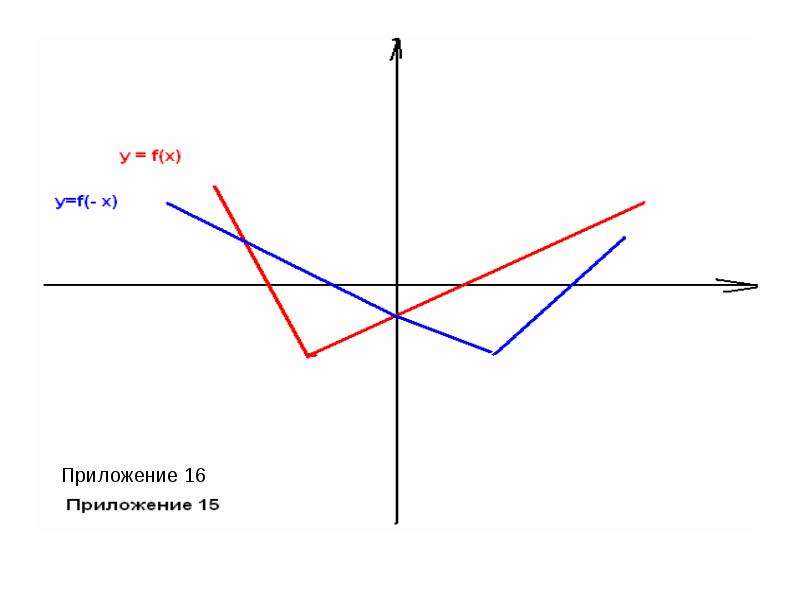
Класс элементарных функции К элементарным функциям относятся практически все функции, встречающиеся в школьном учебнике. Прежде всего, имеется достаточно представительный набор широко известных и хорошо изученных функций, которые называются основными элементарными функциями. Это функции: y=C, называемая константой, y= xа - степенная ( при а = 1 получается функция y=x, называемая тождественной). Графики этих функций прилагаются. (приложение 1-7) Имея в распоряжении основные элементарные функции, можно ввести ряд операций, позволяющих комбинировать их между собой как детали для получения более сложных и разнообразных конструкций. Допустимые арифметические действия над функциями. [+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. Все те функции, которые можно получить из основных элементов с помощью арифметических операций называются элементарными функциями составляют класс элементарных функций.

Образование класса элементарных функций Имея определенный набор базисных функций f1 , f2 ,f3 ,...fk и допустимых операций F1, F2, ... Fs над ними (их разрешается применять любое число раз), мы можем получать другие функции, подобно тому, как из деталей конструктора с помощью определенных правил их соединения можно получить разные модели. Класс всех получаемых таким образом функций обозначается так: < f1,f2,...fk; F1,F2,...Fs>. В частности, если принять за базисные все основные элементарные функции и допустить лишь арифметические операции, то получим класс элементарных функций. Беря в качестве базисных часть основных элементарных функций и допуская, возможно, лишь часть указанных операций, получим некоторые подклассы класса элементарных функций, некоторые семейства функций, порождаемые данным базисом и данными операциями. Вот несколько примеров таких семейств функций, где под (а) понимается операция умножения на любую константу: <x;(*)> - семейство целых положительных степеней у=х, где n € N; <x, 1;(a),(+)> - семейство линейных функций у= ах+в; <x,(a),(+),(*)> - семейство многочленов у= ахn +...+an-1x +an, где n € N.

Построение графиков Чтобы построить график функции у= х +1, надо к графику функции у=х прибавить график функции у=1. В результате график функции у = х сдвинется по оси Оу на 1 единицу вверх (приложение 7).

Построение графиков графика. Для построения графика функции у=х2 достаточно выполнить действие умножение с графиками двух тождественных функций у=х (приложение 8).

Построение графиков Для построения графика функции у= 3х2 надо график функции у= х2 умножить на 3. В результате график функции у= х2 растянется в 3 раза вдоль оси ординат, а если у=0,3 х2 , то произойдет сжатие графика в 0,3 раза вдоль оси Оу. (приложение 8, 9).

Построение графиков График функции у=3(х -4)2 можно получить, выполнив следующие действия: - сложить графики тождественной функции у=х и константы у=-4, получим график функции у=х-4; - перемножить графики функций у=х-4 и у=х-4, получим график функции у= (х -4)2 ; - умножить у= (х -4)2 на 3, получим график функции у=3(х -4)2. Или просто график функции у=3х2 сдвинуть по оси Ох на 4 единичных отрезка (Приложение10).

Преобразования исходного графика функции y= f(x). Из вышесказанного можно сделать следующий вывод, что выполняя различные действия с графиками элементарных функций, мы выполняем преобразования этих графиков, а именно: параллельный перенос, симметрию относительно прямой Ох и прямой Оу.

Преобразования исходного графика функции y= f(x). Параллельный перенос. а)y= f(x)+а – сдвиг по оси Оу на а единиц вверх, если a>0, или вниз, если a<0; б) у=f(x+a) - сдвиг по оси Ох на а единиц влево, если a>0, или вправо, если a<0. (Приложение 11 и 12)

Преобразования исходного графика функции y= f(x). Симметрия относительно оси Ох. а) у=- f(x) – симметричное отражение графика относительно оси Ох; б)у =│f(x)│- замена частей графика, лежащих ниже Ох, отражением относительно этой оси части, лежащей ниже оси Ох, с сохранением остальных частей графика . (Приложение 13 и 14)

Преобразования исходного графика функции y= f(x). Симметрия относительно оси Оу. а) у = f(-x) – симметричное отражение графика относительно оси Оу; б) ) у= f(│x│) – замена части графика, лежащей левее Оу, отражением относительно этой оси части, лежащей правее оси Оу с сохранением правой части графика. (Приложение 15 и 16)

Заключение. Заканчивая свою работу я увидел, что строить графики элементарных функций интересно и просто. А график является портретом функции, поэтому функцию можно назвать поистине красавицей. Математика – это набор инструментов, который необходим в познании окружающего мира. И этим инструментом необходимо владеть в совершенстве, чтобы познавать, развивать и изменять нашу жизнь.

Список литературы. Н.П. Токарчук «Красавицы функции и их графики». В.К.Егоров, Б.А.Радунский, Д.А.Тальский «Методика построения графиков функций». Ю.Н.Макрычев, Н.Г.Миндюк, К.И.Нешков, С.Б,Севорова «Учебник алгебры».