🗊Презентация Метод бесконечного спуска. Решение задач с конечными множествами

Цель: проанализировать возможности метода бесконечного спуска в решении нетривиальных задач. Цель: проанализировать возможности метода бесконечного спуска в решении нетривиальных задач. Задачи: - Показать возможности метода на примере решения важнейших задач школьной алгебры. - Обосновать логическую эквивалентность трёх утверждений: принципа бесконечного спуска, принципа наименьшего элемента и принципа математической индукции. - Обобщить метод бесконечного спуска на случай трансфинитных порядковых чисел (ординалов). - Показать возможности метода бесконечного спуска, обобщённого на случай ординалов, на примере решения нетривиальной задачи.

Простейшая формулировка принципа бесконечного спуска:

2 эквивалентных утверждения.

Принцип математической индукции логически эквивалентен (равносилен) принцип наименьшего числа I. Докажем, что из принципа наименьшего числа следует принцип математической индукции. Проведём доказательство от противного. Пусть для натуральных чисел верен принцип наименьшего числа (мы, например, примем его за исходную аксиому), и для некоторого утверждения А верно А(1). И пусть верно утверждение, что если верно А(k), то и верно А(k+1). Предположим, что утверждение некоторое A(n) верно не при любых натуральных n (принцип МИ не выполняется). Рассмотрим множество тех чисел, для которых оно неверно. В нем есть наименьшее число N. Это число не равно 1, так как A(1) истинно. Но тогда A(N − 1) истинно по выбору N. Значит, и A(N) = A(N − 1 + 1) истинно. Пришли к противоречию.

Историческая справка. Историческая справка. Метод бесконечного спуска изобрели, по-видимому, древнегреческие математики. Метод бесконечного спуска был существенно развит Пьером Ферма. Есть основания полагать, что Ферма пытался доказывать свою Великую теорему именно этим методом.

Теорема: Корень квадратный любого натурального числа является или натуральным, или иррациональным

Геркулес и гидра

Что такое гидра? Гидра - любое конечное дерево, растущее из одного корня. Количество "сыновей" каждой вершины конечно. Головами гидры назовём вершины, не имеющие сыновей. В данном примере головы - B,D,F,G,H.

Как головы отрубают, и как они отрастают? Геркулес отрубает одну из голов гидры. Если у отрубленной головы нет "дедушки", то ничего не происходит и мы переходим к следующему ходу.  

Гипотеза 1. Гидра не способна расти вверх (увеличивать высоту дерева). Жалко её.

Красота задачи в том, что не смотря на простое условие, она требует для решения каких-то новых на первый взгляд не связанных с этой задачей математических абстракций. Красота задачи в том, что не смотря на простое условие, она требует для решения каких-то новых на первый взгляд не связанных с этой задачей математических абстракций. И этой новой абстракцией будет ОРДИНАЛ.

Натуральные числа отвечают на два РАЗНЫХ вопроса: Сколько? - Это количество.

Натуральные числа как указатели порядка.

Ординалы – обобщения порядковых чисел. Ординалы представляют собой обобщение понятия порядковых натуральных чисел. Как и другие разновидности чисел, их можно складывать, перемножать и возводить в степень. Порядковые числа были введены Георгом Кантором в 1883 году.

В основу конструирования ординалов я положила высказывание Г.Кантора

Сконструируем первое трансфинитное число W Представьте себе бесконечную последовательность вертикальных линий, которая имеет начало, и в которой каждая следующая линия короче предыдущей, так же сокращается и расстояние между ними. Понятно, что в какой-то точке такая последовательность обращается в бесконечность, но наш глаз уже не сможет это разглядеть.

Наглядное представление W – первый трансфинитный ординал. W больше любого натурального числа, так как оно включает последовательность из ВСЕХ натуральных чисел.

ω+1 ≠ 1+ω ω+1 ≠ 1+ω Попытайтесь отсчитать бесконечное число раз начиная с линии под номером "1", очевидно же, что до ω+1 вы не досчитаетесь, ибо бесконечность пересчитать невозможно. Значит 1+ω = ω. Умножение транфинитных ординалов некоммутативно: 2⋅ω ≠ ω⋅2 и 2⋅ω = ω. 

Повторим принцип определения. 1 – это ПЕРВОЕ натуральное число. 3 – это ПОСЛЕДОВАТЕЛЬНОСТЬ из двух предыдущих натуральных чисел: 1 и 2 W – это ПОСЛЕДОВАТЕЛЬНОСТЬ из ВСЕХ натуральных чисел. W+1 – это последовательность из всех натуральных чисел и следующего за ними W W+2 – это последовательность из всех натуральных чисел и следующих за ними W и W+1 W+W – это последовательность, включающая все натуральные числа и все трансфинитные числа вида W+N, где N – натуральное число

Выстроим w последовательностей из W

Наглядное изображение W2 W х W=W2 – это бесконечная W -последовательность ординалов W.

Мы получили ординал эпсилон-ноль - ε0. От него тоже можно продолжать дальше и строить, скажем, ε0+1 и т.п., но для решения задачи это уже не нужно. Мы получили ординал эпсилон-ноль - ε0. От него тоже можно продолжать дальше и строить, скажем, ε0+1 и т.п., но для решения задачи это уже не нужно.

Важные свойства построенных ординалов Начиная с w, можно складывать, умножать и возводить в степень друг друга сколько угодно раз, и никогда не выйдешь за пределы ε0. Для всех этих ординалов, включая ε0, справедлив принцип бесконечного спуска.   

Продвинутая формулировка метода бесконечного спуска основана на фундаментальном факте: Не существует бесконечной убывающей последовательности из ординалов.

Вернёмся к гидре

Каждой гидре сопоставим ординал Каждая голова гидры получает значение 0.

Если A - некоторая вершина с детьми, которым мы уже присвоили значения, то расположив  ординалы детей a, b, c, ... u в НЕВОЗРАСТАЮЩЕМ ПОРЯДКЕ, вершине A мы присваиваем значение  wa+wb+...+wu Если A - некоторая вершина с детьми, которым мы уже присвоили значения, то расположив  ординалы детей a, b, c, ... u в НЕВОЗРАСТАЮЩЕМ ПОРЯДКЕ, вершине A мы присваиваем значение  wa+wb+...+wu По определению w0 = 1

Лемма: после каждого хода Геркулеса ординал гидры уменьшается. То есть, если On - ординал гидры после n-го хода, то On+1 < On (неравенство точное!). Лемма: после каждого хода Геркулеса ординал гидры уменьшается. То есть, если On - ординал гидры после n-го хода, то On+1 < On (неравенство точное!).

Выводы. 1. Метод бесконечного спуска (МБС) – это способ доказательства, позволяющий доказывать множество утверждений, например, иррациональность квадратного корня из натуральных чисел. 2. Доказана логическая эквивалентность трёх утверждений: принципа бесконечного спуска, принципа наименьшего элемента и принципа математической индукции. 3. С помощью МБС приведено доказательство утверждения о том, что корень квадратный из натурального числа или натуральный, или иррациональный. 4. Натуральные числа могут служить как для обозначения количества, так и для обозначения порядкового номера. В качестве порядковых чисел их можно обобщить на случай бесконечных вполне упорядочённых множеств - ординалов. 5. Для ординалов не существует бесконечной убывающей последовательности, поэтому их можно использовать для доказательства утверждений с помощью МБС. 6. Ординалы позволяют решать ряд, казалось бы, несложно сформулированных задач, которые, однако, не могут быть решены только применением натуральных чисел: в работе подробно рассмотрена одна такая задача – «Геркулес и Гидра».

Литература Литература 1. Густаво Эрнесто Пинейро Бесчисленное поддается подсчету. Кантор. Бесконечность в математике. / Пер. с итал. — М: Де Агостини, 2015. — 168 с. 2. И. В. Ященко Парадоксы теории множеств. https://www.mccme.ru/mmmf-lectures/books/books/books.php?book=20&page=11\ 3. Николай Вавилов «Не совсем наивная теория множеств». Лекции в ЛГУ. Интернет-источники 1. Mark Kim-Mulgrew Killing the hydra. / https://markkm.com/blog/killing-the-hydra/ 2. https://johncarlosbaez.wordpress.com/2016/06/29/large-countable-ordinals-part-1/ 3. https://www.slideserve.com/abdul-simpson/by-rudolf-fleischer-fudan-university 4. https://digitalccbeta.coloradocollege.edu/pid/coccc:11178/datastream/OBJ 5. https://www.quora.com/Has-anyone-found-more-interesting-propositions-that-cannot-be-proven-true-or-false-based-on-the-discovery-of-G%C3%B6del 6. https://www.youtube.com/watch?v=K1XSZdXydRE

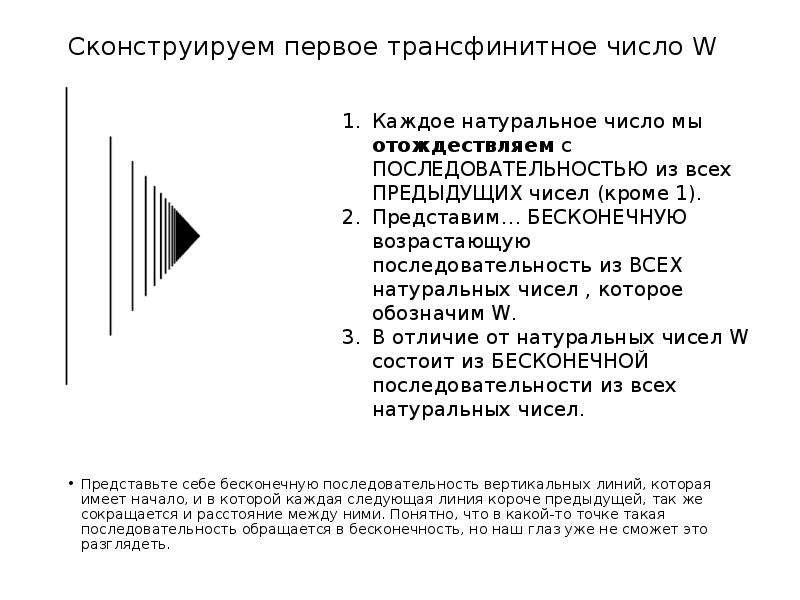
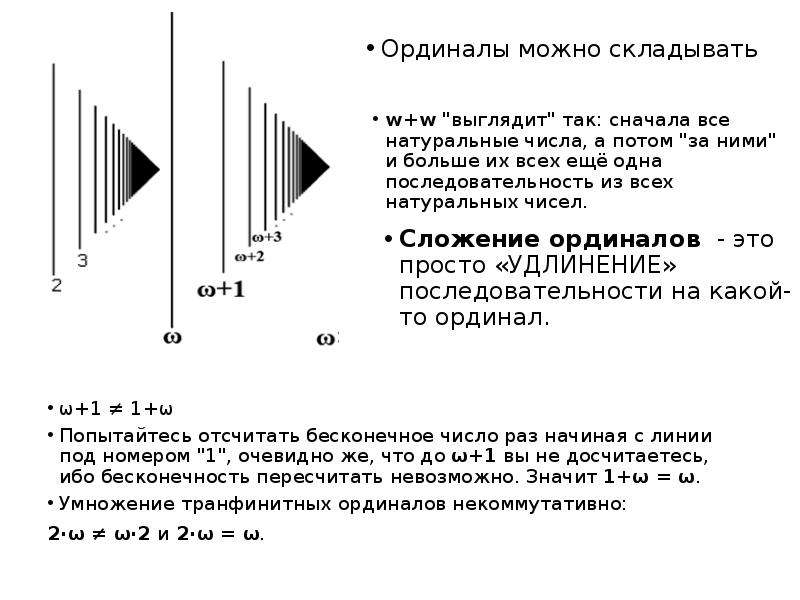
1. Когда вводятся ординалы, то вместо сложения возникает прибавление справа и прибавление слева, это две разные операции. w+1 - новое число, но 1+w = w.  2. Вычитание - это операция, обратная к сложению. Соответственно, есть два вычитания - обратное к прибавлению слева (левое вычитание) и обратное к прибавлению справа (правое вычитание).  Левый случай: w-1 - это ординал X такой, что 1+X=w. Понятно, что X=w. Правый случйй: w-1 - ординал X такой, что Х+1=w. Давайте докажем, что такого X не бывает. Действительно, на не являющихся конечными ординалах задано отношение порядка, и w - минимальный элемент (существует, ибо лемма Цорна). Но Х должен быть меньше w, значит, он конечен. Но после прибавления 1 к конечному числу получается снова конечное, значит, такого Х не существует. Т.е., нельзя вычитать из ординала справа 1, как делить на 0. Ничего не получится. Т.е., можно попробовать, но контекст (частичная упорядоченность + вера в аксиому выбора) рухнет. 1. Когда вводятся ординалы, то вместо сложения возникает прибавление справа и прибавление слева, это две разные операции. w+1 - новое число, но 1+w = w.  2. Вычитание - это операция, обратная к сложению. Соответственно, есть два вычитания - обратное к прибавлению слева (левое вычитание) и обратное к прибавлению справа (правое вычитание).  Левый случай: w-1 - это ординал X такой, что 1+X=w. Понятно, что X=w. Правый случйй: w-1 - ординал X такой, что Х+1=w. Давайте докажем, что такого X не бывает. Действительно, на не являющихся конечными ординалах задано отношение порядка, и w - минимальный элемент (существует, ибо лемма Цорна). Но Х должен быть меньше w, значит, он конечен. Но после прибавления 1 к конечному числу получается снова конечное, значит, такого Х не существует. Т.е., нельзя вычитать из ординала справа 1, как делить на 0. Ничего не получится. Т.е., можно попробовать, но контекст (частичная упорядоченность + вера в аксиому выбора) рухнет.