🗊Презентация Потоки викликів

Лекція 2 ПОТОКИ ВИКЛИКІВ

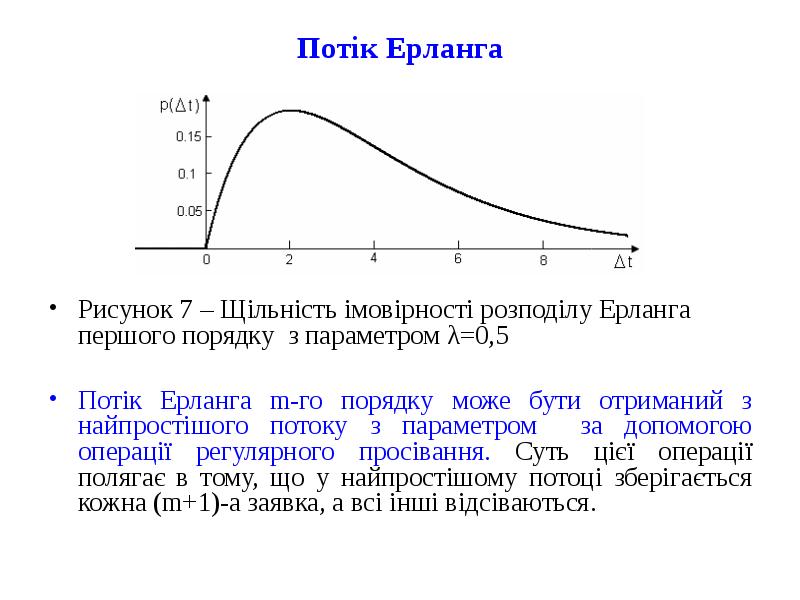
Поняття потоків викликів і основні способи їхнього задання Потоком викликів (заявок) називається послідовність викликів (заявок), що надходять на СРІ в деякі моменти часу [1-5]. Потоки можуть бути детермінованими або випадковими. Детермінований потік – це потік викликів з фіксованими моментами їхнього надходження. Такий потік рідко зустрічається. Якщо моменти надходження викликів залежать від випадкових факторів, то потік називається випадковим. 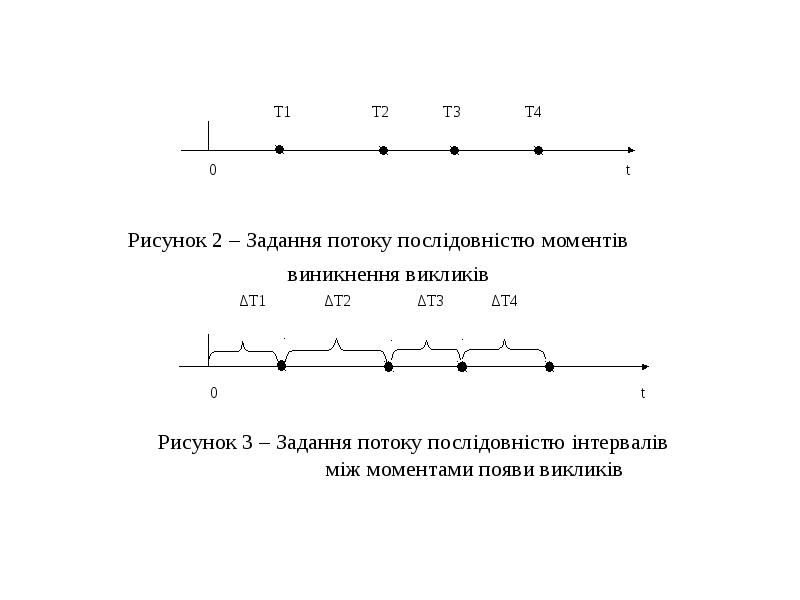Випадковий потік може бути заданий трьома еквівалентними способами: 1) послідовністю моментів виникнення викликів (див. рис. 2); 2) послідовністю інтервалів між сусідніми викликами (див. рис. 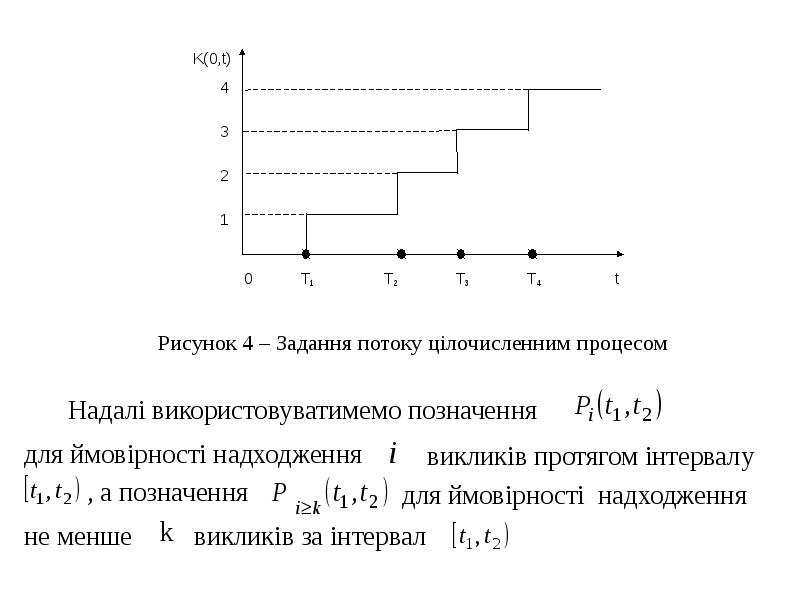3); 3) цілочисленним процесом, що визначає кількість викликів, які надійшли протягом часу [t0, t) (див. рис. 4).

Рисунок 2 – Задання потоку послідовністю моментів виникнення викликів

Імовірнісний опис потоку викликів може бути виконаний з використанням багатовимірних функцій розподілу обраних характеристик потоку. Імовірнісний опис потоку викликів може бути виконаний з використанням багатовимірних функцій розподілу обраних характеристик потоку. До основних числових характеристик потоків викликів належать: провідна функція потоку, інтенсивність і параметр потоку. Провідною функцією потоку Λ(t) називається математичне сподівання числа викликів, що надійшли за інтервал часу , тобто Згідно з означенням,

Під параметром потоку у момент часу t розуміється величина Під параметром потоку у момент часу t розуміється величина

Класифікація потоків викликів відповідно до їх властивостей Потоки викликів класифікуються згідно з такими властивостями, як однорідність, стаціонарність, ординарність і післядія. Розглянемо ці властивості. 1. У неоднорідному потоці кожен виклик має дві і більше характеристики. Наприклад, виклики, що надходять від абонентів телефонної мережі, характеризуються моментами їхнього надходження, напрямками встановлення з'єднань, тривалістю обслуговування й іншими характеристиками. Однорідний потік характеризується лише моментами надходження викликів. На практиці потоки викликів, як правило, є неоднорідними. Однак у теорії розглядаються однорідні потоки, якщо відсутні спеціальні застереження. 2. Властивість стаціонарності потоку означає, що його ймовірнісні характеристики не змінюються в часі.

Потік викликів називається стаціонарним, якщо при будь-якому спільна ймовірність Потік викликів називається стаціонарним, якщо при будь-якому спільна ймовірність надходження викликів за інтервали часу

Потік, що не має цієї властивості, називається неординарним. Потік, що не має цієї властивості, називається неординарним. Приклад ординарного потоку – потік викликів, що надходить на АТС від великої групи абонентів, а прикладами неординарних потоків є потоки телеграм у кілька адрес. 4. Потік викликів називається потоком без післядії, якщо для будь-якого сумісна ймовірність надходження

Іншими словами, відсутність післядії потоку означає незалежність плину випадкового потоку викликів після деякого моменту часу від його плину до цього моменту. Іншими словами, відсутність післядії потоку означає незалежність плину випадкового потоку викликів після деякого моменту часу від його плину до цього моменту. Прикладом потоку без післядії може служити потік телефонних викликів, що надходять від великої групи джерел. Це пов'язано з тим, що лише невелика частина (10-20%) абонентської групи водночас бере участь у з'єднаннях. Потоки, які не мають властивості відсутності післядії, називаються потоками з післядією. Потоки викликів від спарених телефонних апаратів і потоки викликів від малих абонентських груп є прикладами потоків з післядією.

Основні класи потоків Найпростіші потоки Найпростішим потоком називається стаціонарний ординарний потік без післядії. Цей потік є основною моделлю в теорії телетрафіку. Для найпростішого потоку справедлива теорема. Теорема 1. Надходження викликів за інтервал часу тривалістю у найпростішому потоці підпорядковується розподілу Пуассона з імовірностями

У відповідності з зазначеною властивістю найпростіший потік називають також пуассонівським. На рис. 5 наведений приклад розподілу числа викликів за законом Пуассона. У відповідності з зазначеною властивістю найпростіший потік називають також пуассонівським. На рис. 5 наведений приклад розподілу числа викликів за законом Пуассона.

Тоді із властивостей розподілу Пуассона випливають такі наслідки. Тоді із властивостей розподілу Пуассона випливають такі наслідки. 1. . 2. Імовірності пов'язані між собою рекурентним співвідношенням

Якщо Якщо

Теорема 2. У найпростішому потоці інтервали часу між сусідніми викликами є статистично незалежними випадковими величинами з експоненціальним законом розподілу. Їхня функція розподілу Теорема 2. У найпростішому потоці інтервали часу між сусідніми викликами є статистично незалежними випадковими величинами з експоненціальним законом розподілу. Їхня функція розподілу

Щільність імовірності експоненціального розподілу описується виразом Щільність імовірності експоненціального розподілу описується виразом

Нестаціонарний пуассонівський потік викликів Нестаціонарним пуассонівським потоком (або найпростішим потоком із змінним параметром) називається ординарний потік без післядії, у якого параметр

Потоки з обмеженою післядією Потоком з обмеженою післядією називається потік, у якого послідовність інтервалів часу між сусідніми викликами

Потоки з обмеженою післядією У теорії надійності рекурентний потік називається процесом відновлення, а рекурентний потік із запізнюванням – загальним процесом відновлення.

Потоки Пальма Стаціонарний ординарний рекурентний потік із запізнюванням називається потоком Пальма. Потоки Пальма описують виклики, загублені в СРІ. Найпростіший потік є особливим випадком потоку Пальма, у якого всі проміжки часу між викликами, в тому числі і перший, мають експоненціальний розподіл. Існує теорема Пальма, яка стверджує, що якщо на СРІ із втратами та експоненціальним законом розподілу тривалості обслуговування викликів надходять виклики, що утворять потік Пальма, то потік не обслужених викликів є потоком Пальма. Зокрема, якщо вихідний потік найпростіший, то потік загублених викликів буде потоком Пальма.

Потоки Пальма У теорії випадкових потоків показується, що для потоку Пальма випадкові величини мають неперервний розподіл із щільністю ймовірності

Потік Ерланга Потоком Ерланга m-го порядку називається потік Пальма, в якому інтервали між сусідніми викликами – статистично незалежні випадкові величини, розподілені за законом Ерланга m-го порядку, тобто мають неперервний розподіл із щільністю ймовірності

Потік Ерланга Рисунок 7 – Щільність імовірності розподілу Ерланга першого порядку з параметром λ=0,5 Потік Ерланга m-го порядку може бути отриманий з найпростішого потоку з параметром за допомогою операції регулярного просівання. Суть цієї операції полягає в тому, що у найпростішому потоці зберігається кожна (m+1)-а заявка, а всі інші відсіваються.

Потік Ерланга При m=0 розподіл Ерланга збігається з експоненціальним розподілом. При m≥0 розподіл Ерланга має єдиний максимум у точці Δt=m/λ, тому що

Потік Ерланга Потоки Ерланга при різному порядку створюють потоки з різним ступенем випадковості: від найпростішого при m=0 до детермінованого при m=∞. Модель потоку Ерланга застосовують для опису процесів у системах розподілу інформації, коли найпростіший потік викликів розділяється на m+1 напрямок згідно з операцією регулярного просіювання.