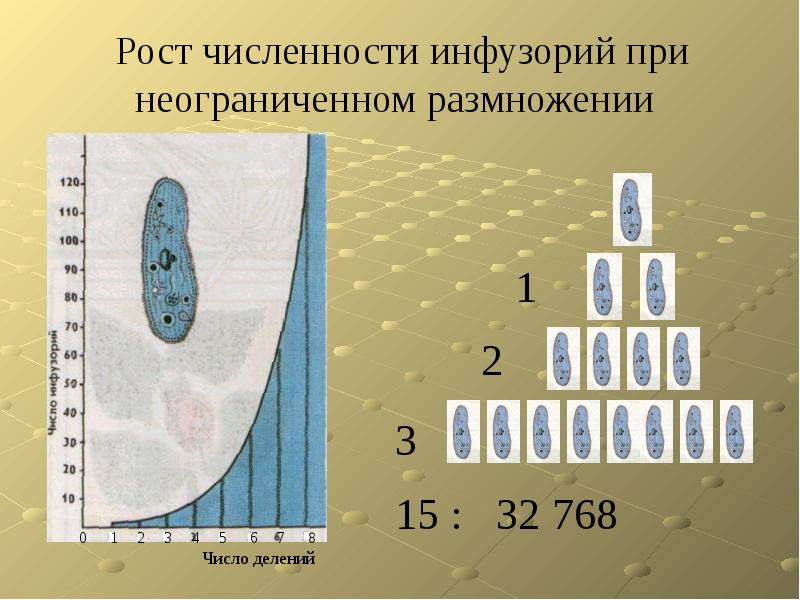
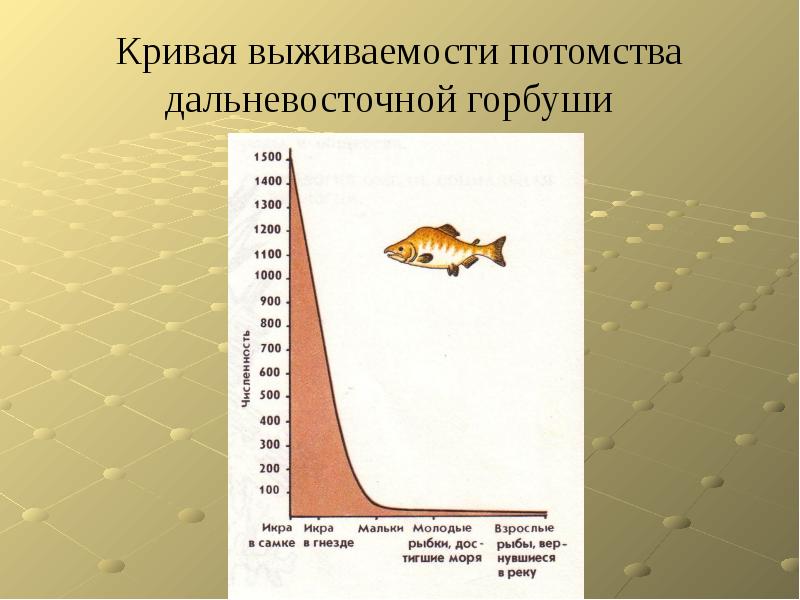
Описание слайда:
1. Сколько надо взять положительных членов арифметической прогрессии 72, 68, 64, …, чтобы их сумма была в 1,4 раза больше суммы бесконечно убывающей геометрической прогрессии, первые два члена которой равны соответственно четвертому и седьмому членам данной арифметической прогрессии?
1. Сколько надо взять положительных членов арифметической прогрессии 72, 68, 64, …, чтобы их сумма была в 1,4 раза больше суммы бесконечно убывающей геометрической прогрессии, первые два члена которой равны соответственно четвертому и седьмому членам данной арифметической прогрессии?
2. За изготовление и установку первого железобетонного кольца для колодца уплачено 10 долларов, а за каждый следующий платили на 2 доллара больше, чем за предыдущий. Кроме того, по окончании работы было уплачено еще 40 долларов. Средняя стоимость изготовления и установки одного кольца оказалась равной доллара. Сколько колец было установлено?
3. Два пешехода вышли одновременно навстречу друг другу и встретились через 3 ч. За какое время пройдет все расстояние каждый из них, если первый пришел в то место, из которого вышел второй, на позже, чем второй пришел в то место, откуда вышел первый?
4. Некоторое положительное число увеличили на 40 %, после чего результат уменьшили тоже на 40 %. Сколько процентов составляет окончательная величина от исходной?
5. Три землечерпалки углубляли фарватер при входе в гавань. Если бы работала только первая из них, то на работу потребовалось бы на 10 дней больше, а если бы только вторая, то на 20 дней больше. При работе одной лишь третьей землечерпалки углубление фарватера заняло бы в 6 раз больше времени, чем при одновременном действии всех трех машин. Сколько времени потребуется для выполнения всей работы каждой землечерпалкой в отдельности?
6. Величина процентного содержания кислоты в трех растворах образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2:3:4, то получится раствор, содержащий 32 % кислоты. Если же смешать их в отношении 3:2:1, то получится раствор, содержащий 22 % кислоты. Сколько процентов кислоты содержит каждый раствор?
7. Маршрут велосипедиста состоит из двух частей: на подъеме он двигается со скоростью 12 км/ч, а затем поворачивает обратно и спускается со скоростью 20 км/ч. Определите среднюю скорость велосипедиста на данном маршруте?
8. Найти арифметическую прогрессию, в которой среднее арифметическое n первых членов равно 2n.
9. Найти сумму членов геометрической прогрессии с 15 по 21 включительно, если сумма первых семи членов прогрессии равна 14, а сумма первых четырнадцати ее членов равна 18.