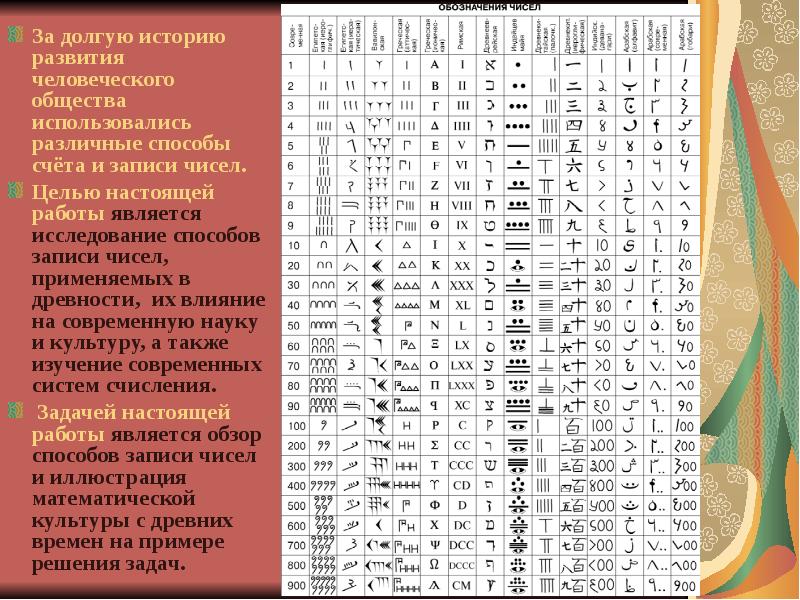
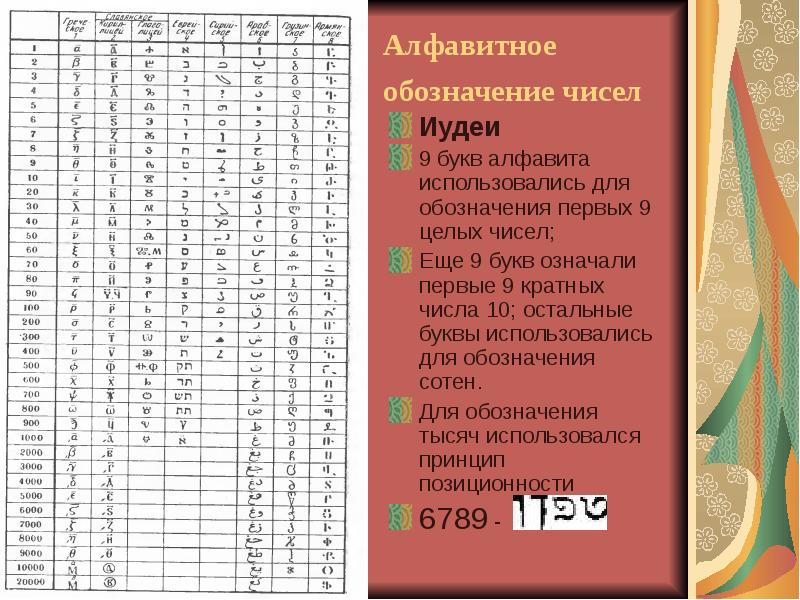
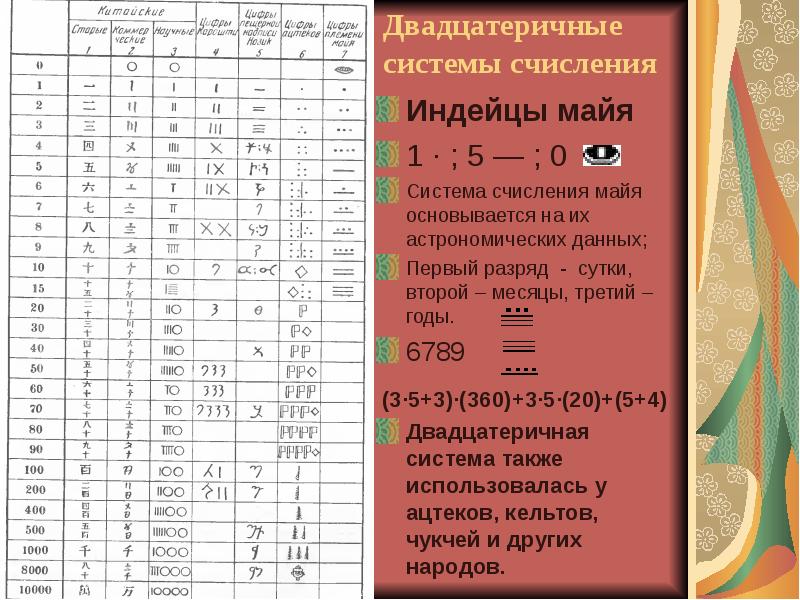
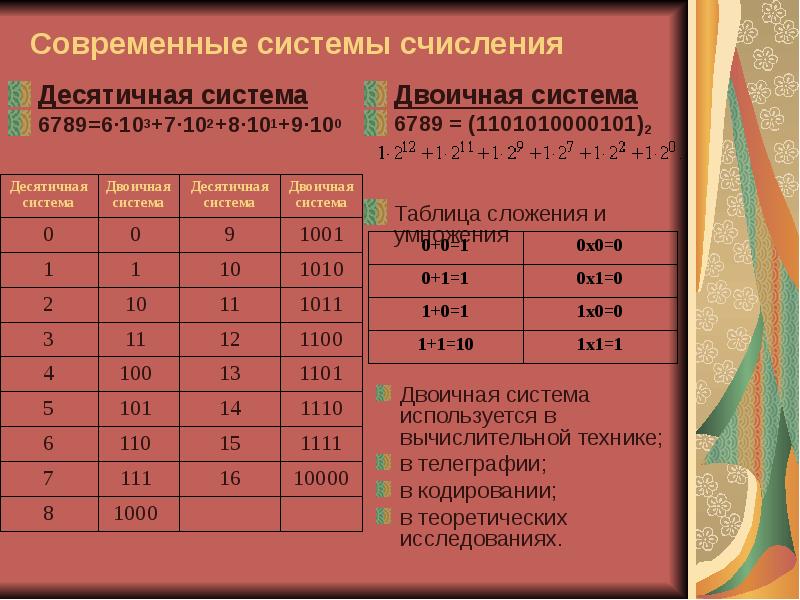
Описание слайда:
Двоичную и троичную систему счисления можно использовать для решения ряда математических задач.
Для взвешивания любого числа граммов песка от 1 г до n г за одно взвешивание, достаточно иметь гири 1 г, 2 г, 4 г, ..., 2m г, где 2m≤n<2m+1, и меньшего числа гирь недостаточно, если песок лежит на одной чашке весов, а гири разрешается ставить на вторую чашку.
Если разрешить класть гири на обе чашки весов, то оптимальной будет система из гирек с массами, образованными степенями тройки (1, 3, 9, 27…). Для того чтобы взвесить груз в n г, надо представить число n в виде суммы a0+3a1+9a2+27a3, где ai=0, ±1 (i=0, 1, 2, 3). Тогда для его взвешивания достаточно на чашку вместе с грузом положить все гири, массы которых входят в эту сумму со знаком минус, а на противоположную чашку положить все гири, массы которых входят в эту сумму со знаком плюс.
Этой задачей интересовался Д. И. Менделеев в бытность свою председателем Российской палаты мер и весов. Частный случай этой задачи был опубликован в книге Баше де Мезириака в XVII веке, а ранее был известен Фибоначчи.
Задача. 12 монет. Из двенадцати монет одиннадцать настоящих, а одна фальшивая (она отличается по весу от настоящей, но не известно, в какую сторону). Требуется за три взвешивания на двухчашечных весах без гирь найти фальшивую монету и выяснить, легче она или тяжелее настоящей.
Решение. Пронумеруем монеты: присвоим им номера 001, 010, 011, 012, 112, 120, 121, 122, 200, 201, 202, 220. Для 1 взвешивания положим на одну чашу весов те монеты, у которых старший разряд равен 0 (то есть 001, 010, 011, 012), а на другую - те монеты, у которых он равен 2 (200, 201, 202, 220). Если перетянет чашка с «0», запишем 0. Если перетянет «2» — запишем 2. Если чаши весов останутся в равновесии — запишем 1. Для 2 взвешивания на одну чашу выложим монеты 001, 200, 201, 202 (то есть все те монеты, у которых второй разряд равен 0), а на другую — 120, 121, 122, 220 (то есть те монеты, у которых средний разряд равен 2). Запишем результат взвешивания. 3 взвешиванием сравниваем 010, 020, 200, 220 с 012, 112, 122, 202 (соответственно, нули и двойки в младшем разряде) и записываем третью цифру. Мы получили 3 цифры —трехзначное число. Далее определяем фальшивую монету так: Если это число совпадает с номером какой-то монеты, то эта монета фальшивая и тяжелее остальных. Если нет, то заменим в этом числе все нули на двойки, а все двойки на нули. После этого оно должно совпасть с номером какой-то монеты. Эта монета фальшивая и легче остальных.