🗊Презентация Статистические методы в психологии. Введение в дисциплину. Понятие измерения. Виды измерительных шкал. Описательные статистики

Статистические методы в психологии. Введение в дисциплину. Понятие измерения. Виды измерительных шкал. Описательные статистики. Закон нормального распределения в психологии. Общие принципы проверки статистических гипотез в психологии. Непараметрические, параметрические критерии. Корреляционный анализ. Многомерные математические методы. Григорьев Павел Евгеньевич Доктор биологических наук, профессор кафедры общей и социальной психологии Института психологии и педагогики ТюмГУ grigorievpe@cfuv.ru www.vk.com/int.research

Дисциплина «Статистические методы в психологии» Цель курса: научиться грамотному использованию методов статистической обработки результатов экспериментальных, научно-практических исследований. Задачи курса: - ознакомить магистров с основными методами статистической обработки психологических данных; - сформировать навыки применения статистических методов; - изучить многомерные методы обработки результатов психологического исследования; - сформировать навыки создания математических моделей в психологии.

Математические методы в психологическом исследовании Научная проверка гипотез экспериментального психологического исследования возможна лишь с привлечением методов теории вероятности и статистики. Поэтому корректное количественное описание психологических явлений, а также верификация и проверка гипотез являются важнейшими сферами применения элементарных математических методов в психологии. Любое исследование предполагает получение качественных результатов (да/нет?) и количественных результатов (насколько?). Наиболее содержательные и точные результаты предполагают количественное (численное) выражение. Но просто собрать данные психологического исследования и представить их в виде чисел недостаточно. Исследователю необходимо организовать данные, обработать их и проинтерпретировать, что невозможно без применения современных математических методов.

Математические методы в психологическом исследовании Для их корректного и результативного использования необходимо: 1) организовать психологическое исследование так, чтобы его результаты были доступны математической обработке в соответствии с проблемами исследования; 2) правильно выбрать метод математической обработки; 3) содержательно интерпретировать результаты обработки. Ценность математического метода определяется теми статистически значимыми, однозначно определенными, клинически или психологически значимыми выводами (об исследованных психологических показателях или явлениях), которые вытекают из результатов математической обработки.

Объект, предмет, свойство, признак, измерение… Следует различать объекты исследования (например, испытуемые с определенными характеристиками), их свойства – то, что в действительности интересует исследователя, составляет предмет изучения, (например, агрессивность) и признаки, отражающие в числовой шкале выраженность свойств (например, число баллов в опроснике Басса-Дарки измерения уровня агрессивности). Признак – реально измеряемое явление, в той или иной степени отражающее интересующее исследователя свойство изучаемого объекта. Измерение – это приписывание объекту числа или знака по определенному правилу. Это правило устанавливает соответствие между измеряемым свойством объекта и результатом измерения – признаком. Точность, с которой признак отражает измеряемое свойство, зависит от процедуры измерения.

Объект, предмет, свойство, признак, измерение… Любое исследование в зависимости от того, насколько надежны полученные в нем результаты и насколько они применимы на практике, можно охарактеризовать с двух точек зрения: достоверности (внутренней обоснованности); о6общаемости (внешней обоснованности, применимости). Достоверность исследования определяется тем, в какой степени структура и методы исследования соответствует поставленным задачам, а полученные результаты справедливы в отношении изучавшейся выборки. Обобщаемость результатов исследования отражает, в какой мере результаты данного исследования применимы к другим (прежде всего, аналогичным, но и другим в некоторых отношениях) группам.

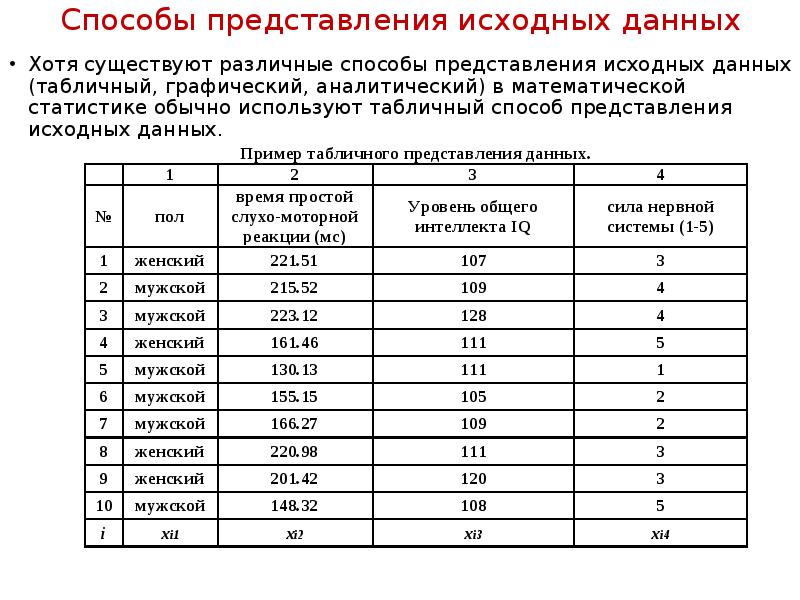
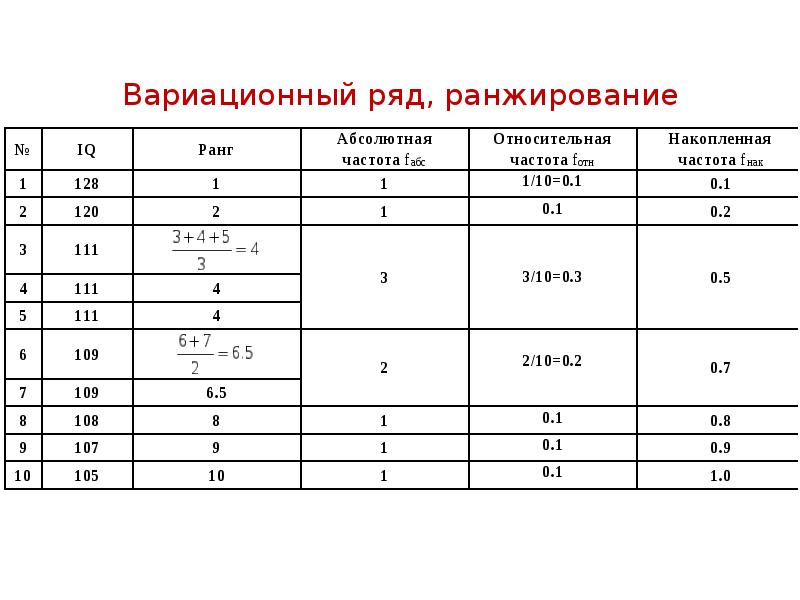
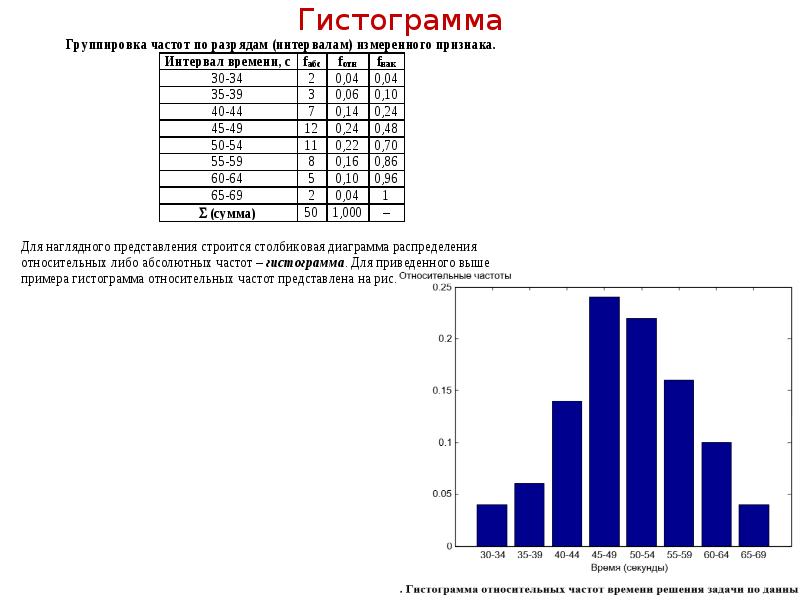
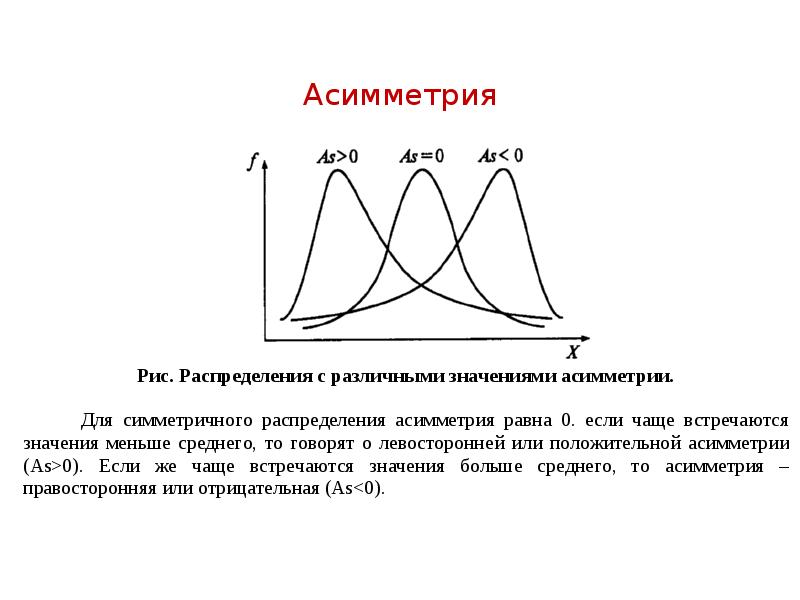
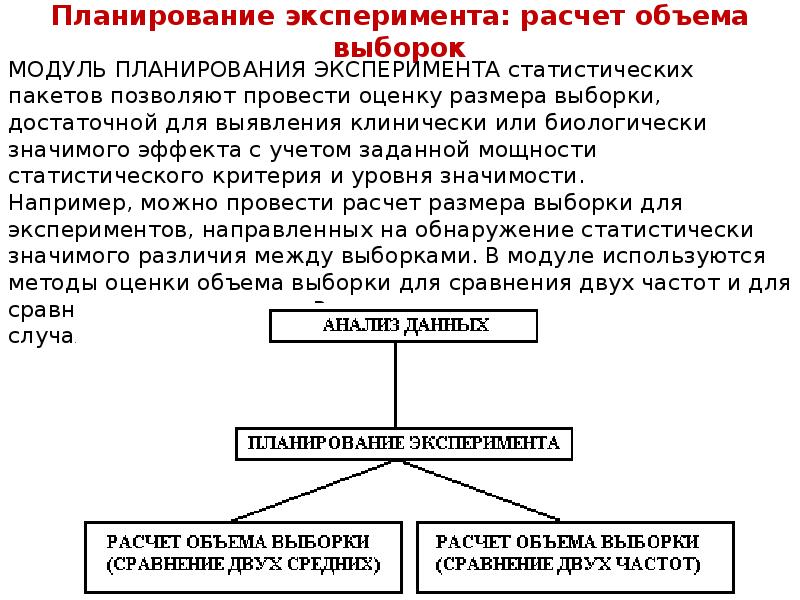
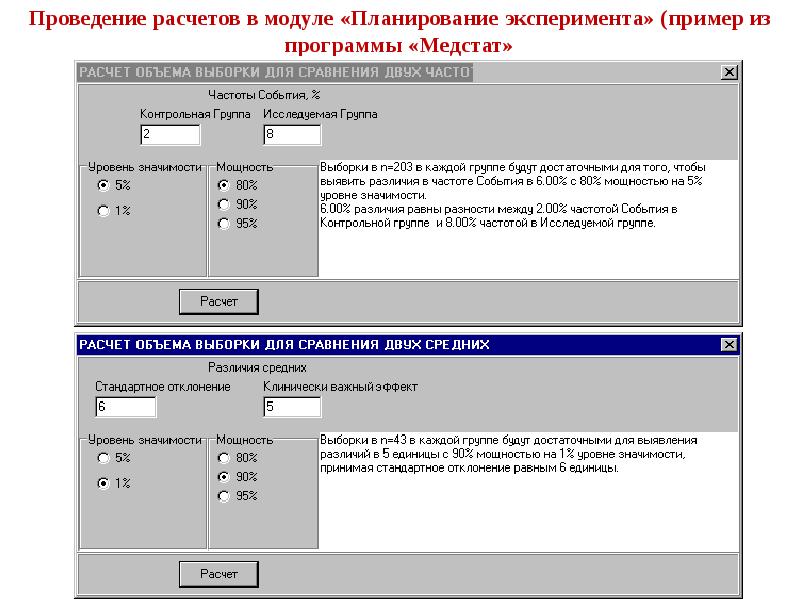
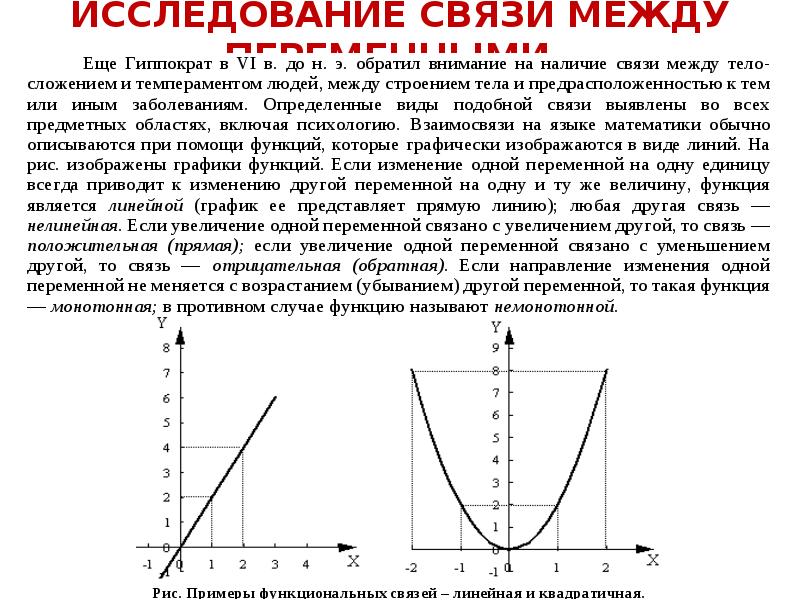
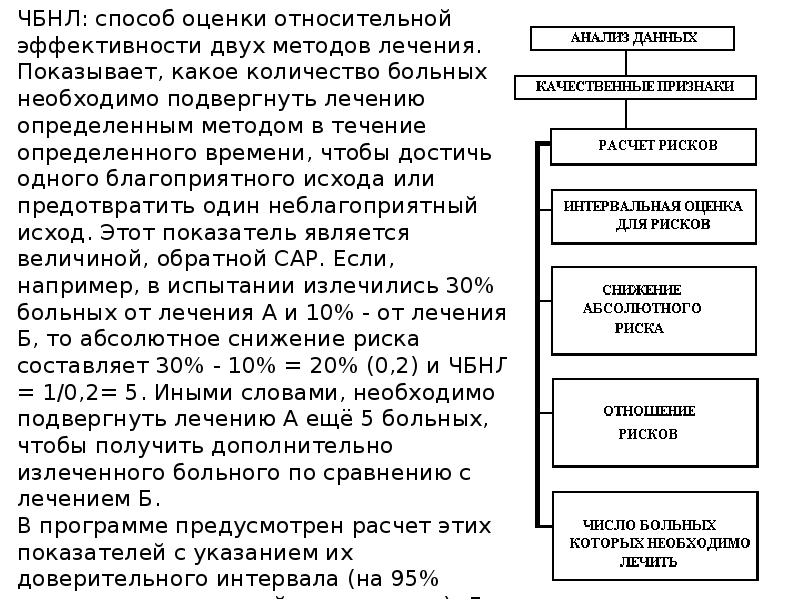
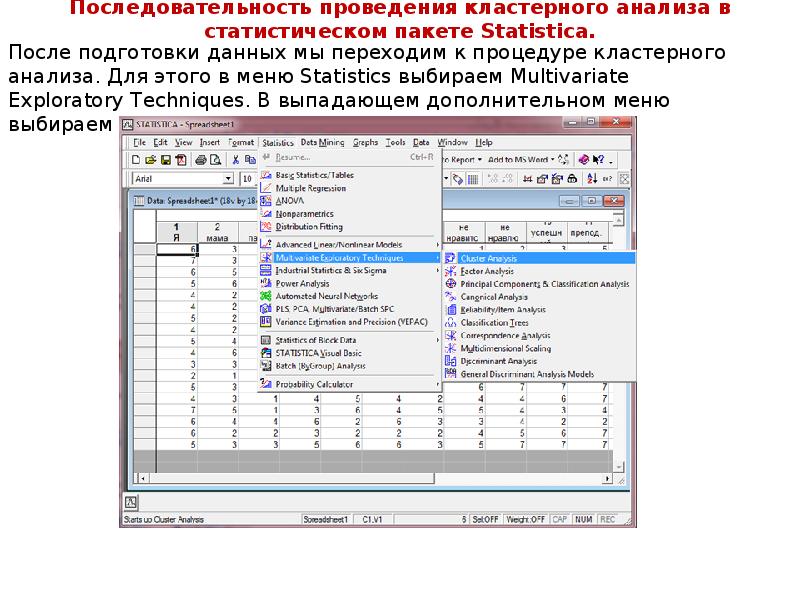
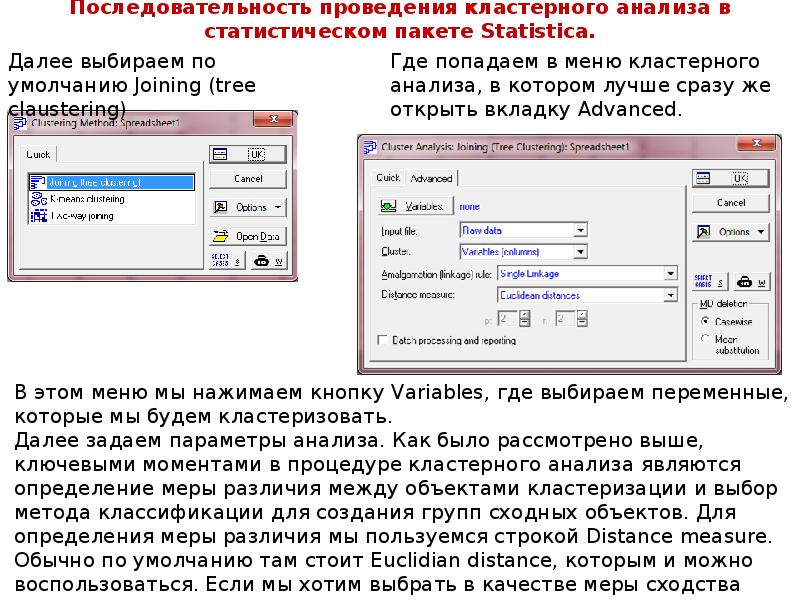
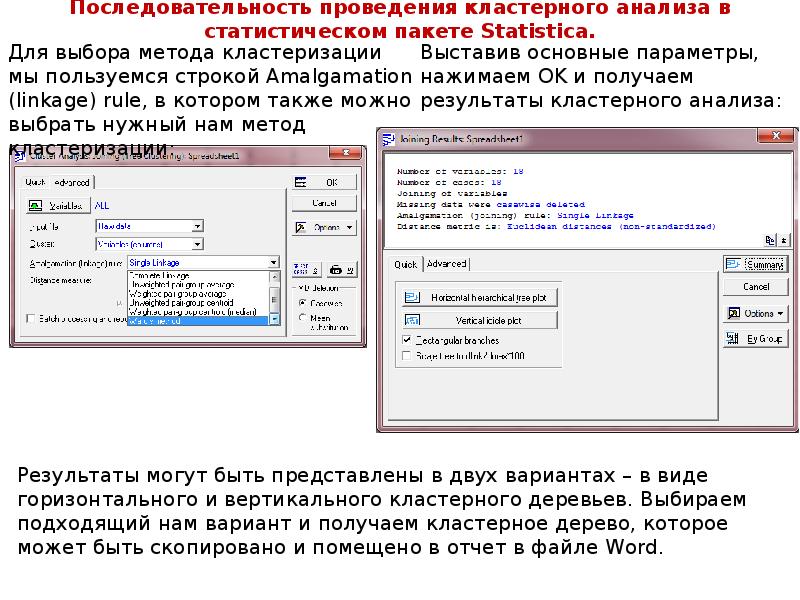
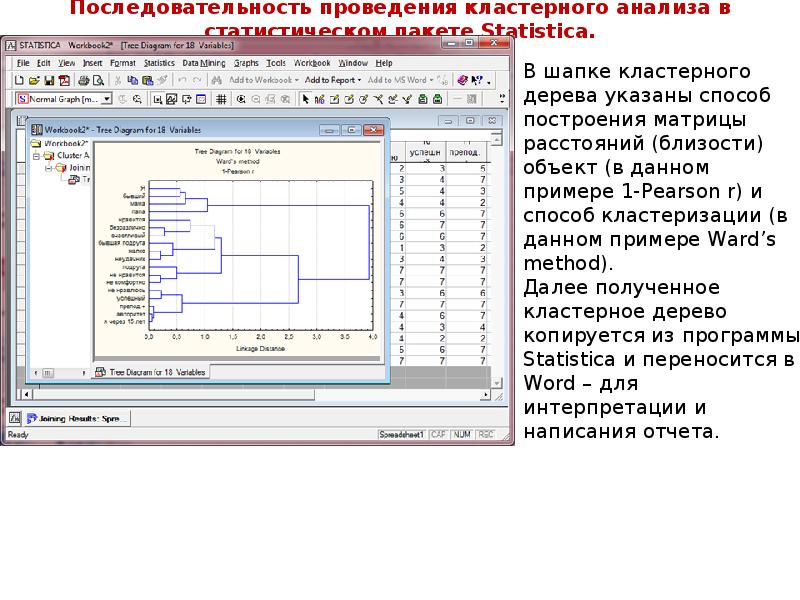
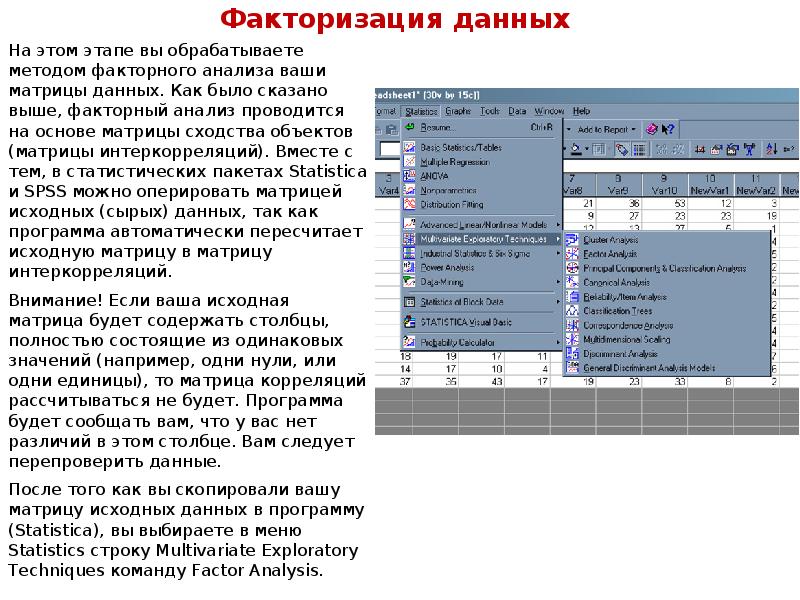
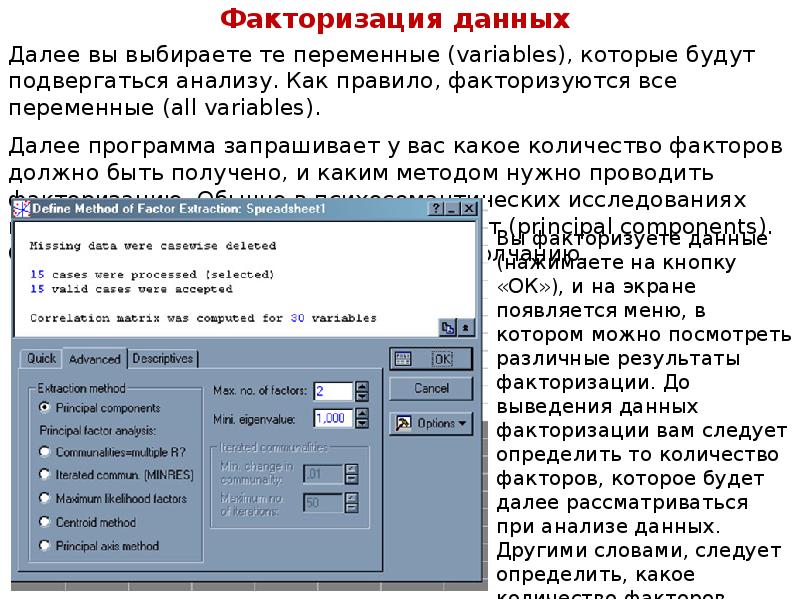
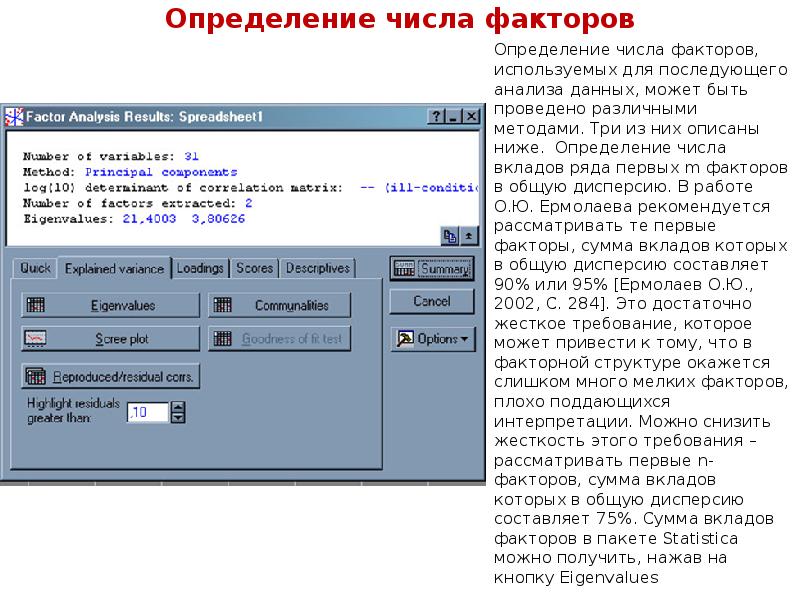
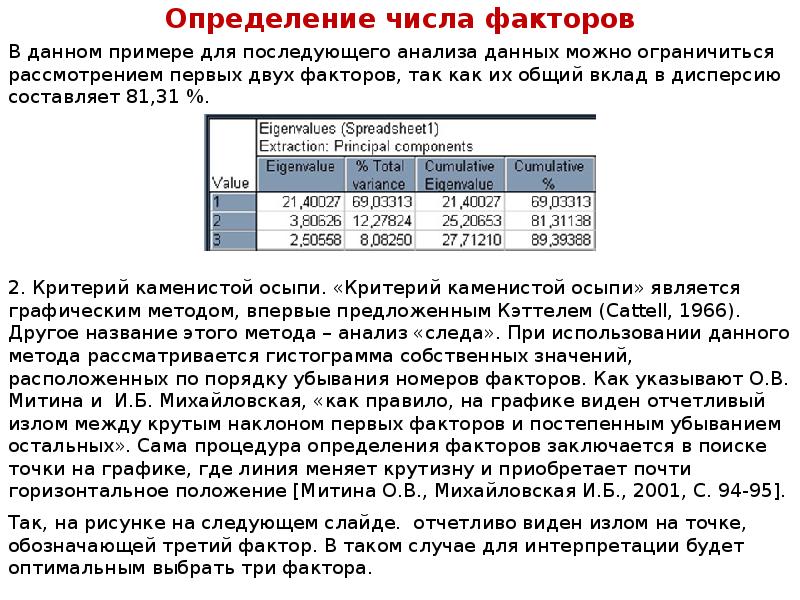
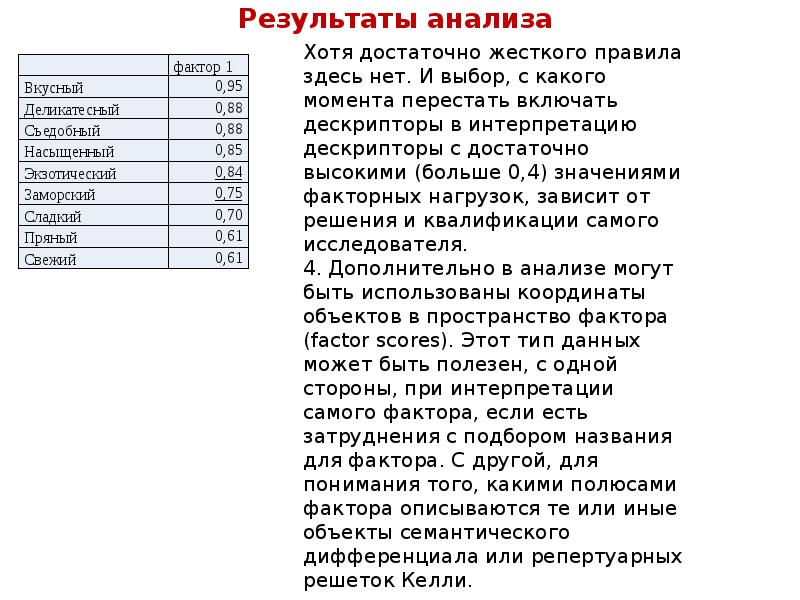
Особенности статистического описания и метода Статистическое описание совокупности объектов занимает промежуточное положение между индивидуальным описанием каждого из объектов совокупности (например, описание конкретного случая работы с клиентом), с одной стороны, и описанием совокупности по её общим свойствам (например, только общие черты, присущие всем представителям некоторой субпопуляции, например, подросткам с возбудимой психопатией), совсем не требующим её расчленения на отдельных субъектов, – с другой. Статистические данные всегда в большей или меньшей степени обезличены и имеют лишь ограниченную (особенно в практическом отношении) ценность в случаях, когда наиболее существенны именно индивидуальные данные.

Особенности статистического описания и метода Обычно применение статистического метода предусматривает: 1) подсчёт числа объектов, входящих в те или иные группы; 2) рассмотрение распределения признаков; 3) применение выборочного метода (в случаях, когда детальное исследование всех объектов обширной генеральной совокупности затруднительно); 4) использование теории вероятностей при оценке достаточности числа наблюдений для тех или иных выводов.

Особенности статистического описания и метода Психологическое исследование обычно начинается с некоторой гипотезы, требующей проверки с привлечением фактов. Гипотеза формулируется в отношении связи явлений или свойств в некоторой совокупности объектов. Например, исследователь может предположить, что женщины в среднем более тревожны, чем мужчины (тревожность связана с полом). Или что аддикция компьютерными играми со сцены насилия, повышает агрессивность подростков. В первом случае исследователя интересуют связь свойств тревожности и пола, во втором – связь явления увлечения играми со свойством агрессивности. Объектами-носителями свойств в первом случае в пределе будут все мужчины и женщины, во втором все подростки. Для проверки подобных предположений на фактах необходимо измерить соответствующие свойства у их носителей-объектов. Но невозможно измерить тревожность у ВСЕХ мужчин и женщин в мире, как невозможно измерить агрессивность у ВСЕХ подростков, в разной степени увлеченными или не увлеченными играми с насилием! Поэтому при проведении исследования ограничиваются лишь относительно небольшой группой представителей соответствующей совокупности людей.

Генеральная совокупность и выборка Генеральная совокупность – это все множество объектов, в отношении которого формулируется исследовательская гипотеза. Необязательно генеральные совокупности огромны по численности объектов. Например, при изучении профессионального самоопределения студентов-выпускников факультета психологии в конкретном вузе генеральная совокупность невелика и допускает сплошное (а не выборочное) исследование. Но исследователь обычно надеется, что выводы исследования будут справедливы (ДОСТОВЕРНЫ) не только в отношении выпускников этого, но и последующих годов (ОБОБЩАЕМЫ). Таким образом, генеральная совокупность – это хотя и не бесконечное по численности, но, как правило, недоступное по тем или иным причинам для сплошного исследования множество потенциальных испытуемых. Выборка – это ограниченная по численности группа объектов (в психологии – испытуемых, респондентов), специально отбираемая из генеральной совокупности для изучения ее свойств. Соответственно, изучение на выборке свойств генеральной совокупности называется выборочным исследованием. Почти все психологические исследования являются выборочными, а их выводы распространяются на генеральные совокупности.

Генеральная совокупность и выборка Таким образом, после того, как сформулирована гипотеза и определены соответствующие генеральные совокупности, перед исследователем возникает проблема организации выборки. Выборка должна быть такой, чтобы была обосновано обобщение выводов выборочного исследования, распространение их на генеральную совокупность. Основные критерии обоснованности выводов исследования: репрезентативность выборки; статистическая значимость или иначе говоря достоверность (эмпирических) результатов. Репрезентативность (представительность) выборки – это способность выборки представлять изучаемые явления достаточно полно. Конечно, полное представление об изучаемом явлении, во всем его диапазоне и нюансах изменчивости, может дать только генеральная совокупность. Поэтому репрезентативность всегда ограничена в той мере, в какой ограничена выборка.

Репрезентативность выборки Приемы, позволяющие получить достаточную репрезентативность выборки: Простой случайный (рандомизированный) отбор. Он предполагает обеспечение таких условий, чтобы каждый член генеральной совокупности имел равные с другими шансы попасть в выборку. Слу­чайный отбор обеспечивает возможность попадания в выборку самых разных представителей генеральной совокупности. При этом принимаются специ­альные меры, исключающие появление какой-либо закономерности при отборе. Например, изучая агрессивность подростков, исследователь может случайным образом остано­вить свой выбор на 3 классах разных школ и затем случайным образом отобрать по 10 учащихся из каждого класса. Если же исследователь просит испытуемого пригласить на обследование своих друзей, он грубо нарушает принцип случайности отбора. Стратифицированный случайный отбор, или отбор по свойствам генеральной совокупности. Он предполагает предварительное определение тех качеств, которые могут вли­ять на изменчивость изучаемого свойства (это может быть пол, уровень дохо­да или образования и т. д.). Затем определяется процентное соотношение чис­ленности различающихся по этих качествам групп (страт) в генеральной совокупности и обеспечивается идентичное процентное соотношение соот­ветствующих групп в выборке. Далее в каждую подгруппу выборки испытуе­мые подбираются по принципу простого случайного отбора. Например, исследователь может предположить, что мальчики и девочки различаются как по агрессивности, так и по восприимчивости демонстрируемых по телеви­дению сцен насилия. Если исследователь планирует обобщить результат ис­следования влияния телевидения на агрессивность всех подростков, то, руко­водствуясь социально-демографическими данными, он должен обеспечить идентичное генеральной совокупности соотношение мальчиков и девочек в выборке.

Статистическая достоверность (значимость) Статистическая достоверность (значимость) результа­тов исследования определяется при помощи методов статистического выво­да (рассмотрим это далее). Они предъявляют определенные требования к численности, или объему выборки. Однозначных рекомендаций по предварительному определению требуемого объема выборки не существует. Тем не менее, можно сформулировать наиболее общие рекомендации: при разработке диагностичес­кой методики необходим наибольший объем выборки – от 200 до 1000-2500 человек; при сравнении 2 выборок их общая численность должна быть не менее 50 человек, численность сравниваемых выборок должна быть приблизительно одинаковой; при изучении взаимосвязи между какими-либо свойствами, то объем выборки должен быть не меньше 30-35 человек. Кроме того, чем больше изменчивость изучаемого свойства, тем больше должен быть объем выборки. Поэтому изменчивость можно уменьшить, увеличивая однородность выборки, например, по полу, возрасту и т. д. При этом уменьшаются возможности обобщения (генерализации) выводов.

Зависимые и независимые выборки Обычна ситуация исследования, когда интересующее исследователя свойство изучается на двух или более выборках с целью их дальнейшего сравнения. Эти выборки могут находиться в различ­ных соотношениях — в зависимости от процедуры их организации. Независи­мые выборки характеризуются тем, что вероятность отбора любого испытуе­мого одной выборки не зависит от отбора любого из испытуемых другой выборки. Напротив, зависимые выборки характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки. Наиболее типичный пример зависимых выборок — повторное измерение свойства (свойств) на одной и той же выборке после воздействия (ситуация «до-после»). В этом случае выборки (одна – до, другая – после воздействия) зависимы в максимально возможной степени, так как они включают одних и тех же испытуемых. Могут быть и более слабые варианты зависимости. Например, мужья – одна выборка, их жены – другая выборка (при исследовании, например, их предпочтений). Или: дети 5-7 лет – одна выборка, а их братья или сестры-близнецы — другая выборка. В общем случае зависимые выборки предполагают попарный подбор ис­пытуемых в сравниваемые выборки, а независимые выборки — независимый отбор испытуемых.

Обзор классификаций признаков Качественные, количественные. Метрические, неметрические. Принадлежность к одной из шкал: Номинативная, порядковая, интервальная, абсолютная. По роли в статистической совокупности: факторные, результирующие. Признаки сходства (общие для статистической совокупности признаки), признаки различия (индивидуальные особенности каждой единицы наблюдения). По выбору в качестве единицы наблюдения случая (например, заболевания) или полицевого учета.

Различные шкалы в психологических исследованиях В зависимости от того, какая операция лежит в основе измерения признака, выделяют различные типы измерительных шкал. Шкалы разделяют на метрические (если может быть установлена единица измерения) и неметрические (если единицы измерения не могут быть установлены). Номинативная шкала или шкала наименований (относится к неметрическим шкалам). Пользуясь определенным правилом, объекты группируются по различным классам так, чтобы внутри класса они были идентичны по измеряемому свойству. Затем каждому классу и объекту дается наименование и обозначение. Примеры номинативных признаков: «пол» (1 – мужской, 0 - женский); «национальность» (1 – русский, 2 – украинец, 3 – белорус); «предпочтение домашних животных» (1 – собаки, 2 – кошки, 3 – крысы, 4 – попугаи, 0 – никакие). В этом случае учитываются только одно свойство чисел – то, что это разные символы. Операции с числами, такие как упорядочивание, сложение-вычитание, умножение-деление, при измерении в номинативной шкале теряют смысл. При сравнении объектов мы можем сделать вывод только о том, принадлежат они к одному или разным классам, тождественны они или нет по измеренному свойству.

Различные шкалы в психологических исследованиях Порядковая (ранговая) шкала (относится к неметрическим шкалам). Измерение в этой шкале предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства. Примеры признаков, выраженной в порядковой шкале: «место в рейтинге» (от первого до последнего); «оценка за экзамен» (от 2 до 5); и большинство иных измерений в психологических исследованиях (где не проведена стандартизация и обоснование процедуры равноинтервальности)! При сравнении испытуемых друг с другом мы можем сказать, больше или меньше выражено свойство, но не можем сказать, насколько или во сколько раз больше или меньше оно выражено. При измерении в порядковой шкале из всех свойств чисел учитывается лишь то, что они разные и то, что одно число больше другого. Например, если шкалой является распределение результатов участников гонки по местам от первого до последнего, то это вовсе не значит, что они достигали финиша через равные интервалы времени.

Различные шкалы в психологических исследованиях Интервальная шкала (относится к метрическим шкалам). При таком измерении числа отражают не только различия между объектами в уровне выраженности свойства (как в порядковой шкале), но и то, насколько больше или меньше выражено свойство. Равным разностям между числами в этой шкале соответствуют равные разности в уровне выраженности измеренного свойства, т.е. измерение в этой шкале предполагает возможность применения единицы измерения (метрики). Объекту присваивается число единиц измерения, пропорциональное степени выраженности измеряемого свойства. При этом нулевая точка не соответствует полному отсутствию измеряемого свойства. При сравнении двух объектов мы можем судить, насколько больше или меньше выражено свойство, но не можем судить о том, во сколько раз больше или меньше выражено свойство. Примеры измерения в интервальной шкале: температурная шкала Цельсия (где точка нуля – не полное отсутствие температуры, а всего лишь температура замерзания воды); многие тестовые шкалы, вводимые при обосновании равноинтервальности, как шкала IQ Векслера (ноль по этой шкале вовсе не соответствует полному отсутствию интеллекта как такового), некоторые виды семантического дифференциала, и т.п.

Различные шкалы в психологических исследованиях Шкала отношений или абсолютная шкала (относится к метрическим шкалам). Отличается от интервальной только тем, что в ней устанавливается нулевая точка, соответствующая полному отсутствию измеряемого свойства. Примеры измерений в шкале отношений: измерение времени реакции, роста, веса, температуры по абсолютной шкале (где «0» означает совершенное отсутствие температуры) и т.п. Сравнивая результаты, измеренные в этой шкале, между собой, можно сказать не только, насколько больше или меньше выражено данное свойство, но и во сколько раз. Вышеперечисленные шкалы отличаются по их мощности – сколько информации о различии объектов можно получить при помощи признака, выраженного в разных шкалах. По мере возрастания мощности в этом отношении данные шкалы располагаются следующим образом: номинативная, порядковая, интервальная, шкала отношений. Очевидно, наиболее тонкие различия между объектами можно выявить с помощью метрических шкал, неметрические шкалы дают более грубые интерпретации при сравнении объектов.

Различные шкалы в психологических исследованиях Определение того, в какой шкале измерено явление – первостепенный момент анализа данных: любой последующий шаг, выбор метода зависит именно от этого. Обычно идентификация номинативной шкалы от других шкал не представляет трудностей. Сложнее определить различие между порядковой и интервальной шкалами. В психологии часто по степени выраженности непосредственно измеряемой величины (например, количество правильных ответов на вопросы) выносят суждения о некотором скрытом свойстве (например, интеллекте), недоступном прямому наблюдению. Таким образом, большинство измерений в психологии являются косвенными. Например, количество правильных ответов на вопросы – это измерение в метрической шкале, но соответствуют ли равные разности количества правильных ответов равным разностям выраженности интеллекта? Если это так, то шкала интервальная и метрическая, если нет – то шкала порядковая и неметрическая. В ряде случаев имеет смысл обосновывать метричность (равноинтервальность) шкалы для того, чтобы иметь возможность использовать более мощные инструменты анализа данных.

Некоторые элементарные типы задач психологического исследования (с точки зрения статистического метода) Выявление различий в уровне исследуемого признака. Сопоставляются различные группы испытуемых по какому-то признаку, чтобы выявить различия между ними по этому признаку (например, сопоставляются показатели вербального интеллекта у студентов-психологов и студентов-физиков). Оценка сдвига значений исследуемого признака. Чаще всего у одной и той же группы испытуемых сопоставляются уровни признака «до» и «после» экспериментальных или иных воздействий (или же по прошествии определенного времени, или в разных условиях, например, обычных и экстремальных), чтобы определить эффективность этих влияний (например, сопоставляются уровни самооценки участников терапевтической группы до и после тренинга).

Некоторые элементарные типы задач психологического исследования (с точки зрения статистического метода) 3. Выявление различий в распределении признака. Сопоставляется эмпирическое распределение значений признака с каким-либо теоретическим законом распределения или два эмпирических распределения между собой (например, отличается ли распределение показателей показателя тревожности от равномерного по дням недели; отличается ли соотношение успевающих и неуспевающих школьников в зависимости от того, полная ли у них семья, и т.д.). 4. Выявление степени согласованности изменений нескольких признаков или профилей. Могут быть сопоставлены два признака, измеренные на одной и той же выборке испытуемых для того, чтобы установить степень согласованности их изменений (корреляцию) между ними (например, выясняется наличие связи уровней социального интеллекта и тревожности у студентов-психологов). Следует отметить, что наличие различий или корреляционной связи вовсе не означает автоматически наличия причинно-следственных связей.

Упражнения Определите, в какой шкале представлено каждое из приведенных ниже измерений: номинативной, порядковой, интервальной, отношений? Обоснуйте ответ. порядковый номер испытуемого в списке (для его идентификации); количество вопросов в анкете как мера трудоемкости опроса; упорядочивание испытуемых по времени решения тестовой задачи; академический статус (ассистент, доцент, профессор) как указание на принадлежность к соответствующей категории; академический статус (ассистент, доцент, профессор) как мера продвижения по службе; телефонные номера; время решения задачи; количество агрессивных реакций за рабочий день; количество агрессивных реакций за рабочий день как показатель агрессивности; цвет глаз; числа, кодирующие темпераменты; метрическая система измерения расстояний.

Упражнения Определите, к какому типу задач на сопоставление следует отнести нижеперечисленные задачи и почему? Установить эффективность лечения депрессии, сравнивая ее показатели до и после применения определенной терапии в группе испытуемых; Определить характер связи между агрессивностью и тревожностью у группы подростков; Как отличаются студенты-физики от студентов-психологов по уровню вербального интеллекта? Как отличаются между собой по уровню тревожности дети из полных и неполных семей? Различны ли показатели настроения у студентов до и после экзаменационной сессии? Существует ли связь между ростом человека и его заработной платой? Достигнуть вершины можно по нескольким маршрутам. Существуют ли предпочтения относительно выбора какого-либо из путей? Равномерно ли распределяются частоты обращений в службу психологической помощи по разным дням недели? Зависят ли показатели воспроизведения слов испытуемыми, которые предъявлялись им на слух, от скорости их предъявления?

Научно-исследовательская работа: помощь, участие, направления квалификационных (курсовых, дипломных) работ, выполняемых под руководством профессора Григорьева Павла Евгеньевича и доцента Васильевой Инны Витальевны Исследования различных аспектов интуиции у представителей различных групп (возраст, пол, потребности, особенности физиологического статуса и проч.) с помощью психологических, программно-аппаратных методов и методик Психофизиологические исследования функционального состояния представителей различных групп в зависимости от нагрузок, ситуации, деятельности Разработка новых методов улучшения эффективности деятельности представителей опасных и связанных с повышенной ответственностью профессий в условиях дефицита времени и/или информации Вступайте в группу «Intuition & Intention» www.vk.com/int.research Принимайте участие в обсуждениях, играйте в игру «Мир магии», а также других исследованиях интуиции (18+)

Вопросы для проработки и самостоятельного изучения Понятие измерения. Виды измерительных шкал и свойства психологических объектов измерения. Номинативная шкала как способ классификации или распределения объектов. Порядковая шкала как способ расположения измеряемых признаков по рангу. Правила ранжирования. Шкала интервалов и её свойства. Распределение значений по принципу: «больше на определенное количество единиц – меньше на определенное количество единиц». Шкала (равных) отношений, ее особенности. Наличие фиксированного нуля. Понятие генеральной совокупности. Понятие выборки как подгруппы элементов (испытуемых), выделенной из генеральной совокупности для проведения эксперимента. Объем выборки. Полное (сплошное) и выборочное исследование. Зависимые и независимые выборки. Требования к выборке при решении различных задач. Репрезентативность выборки. Формирование и объем репрезентативной выборки.

Рекомендованная для закрепления материала лекций литература Р. Майкл Фер, Верн Р. Бакарак. Психометрика: Введение; пер. с англ… Челябинск: Издательский центр ЮУрГУ, 2010. 445 с. https://yadi.sk/d/rXZGxdvxuxB6n Лакин Г.Ф. Биометрия. М.: Высшая школа, 1990. 352 с. https://yadi.sk/d/gOx4ndnSuxBHB Сидоренко Е.В. Методы математической обработки в психологии. СПб: Речь, 2006. 348 с. https://yadi.sk/i/0SV19sefuxBY9 Остапенко Р.И. Математические основы психологии. Учебно-методическое пособие. Воронеж: ВГПУ, 2010. 76 с. https://yadi.sk/i/LoZ57-O6uxDfg Червинская К.Р. Компьютерная психодиагностика. СПб: Речь, 2003. 336 с. https://yadi.sk/d/8ln7_Hk9uzxLA

Способы представления исходных данных Хотя существуют различные способы представления исходных данных (табличный, графический, аналитический) в математической статистике обычно используют табличный способ представления исходных данных.

Вариационный ряд, частоты

Вариационный ряд, ранжирование Предположим, что исследователя в нашем примере интересует распределение уровня интеллекта учащихся. Для этого исходный ряд упорядочивается от максимального до минимального значения или наоборот. При этом большему значению может быть приписан больший или меньший ранг (место по порядку). Так, в таблице на следующем слайде ряд значений IQ расположен в убывающем порядке, наибольшему значению приписан ранг 1. Если несколько значений одинаковы, они имеют одинаковый ранг, равный среднему арифметическому тех рангов, которые они получили бы, если бы не были равны.

Вариационный ряд, ранжирование

Таблицы распределения накопленных частот

Гистограмма

Описательные статистики

Меры центральной тенденции

Меры центральной тенденции

Меры положения

Меры изменчивости

Меры изменчивости, стандартизация

Стандартизированные шкалы, асимметрия

Асимметрия

Эксцесс

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез. История применения закона нормального распределения в социальных и биологических науках начинается, с работы бельгийского ученого А.Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как продолжительность жизни, возраст вступления в брак и появления первого ребенка и т.д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые отклонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. В его исследованиях, и позднее — в исследованиях Ф. Гальтона, было доказано, что распределение частот встречаемости любого демографического (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большой выборке людей, имеет одну и ту же «колоколообразную» форму.

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ В дальнейшем трудами Ф. Гальтона и его последователей было доказано, что и психо­логические особенности, например, способности, подчиняются нормальному закону. Поэтому дальнейшее развитие измерительного подхода в психологии и статистичес­кого аппарата проверки гипотез происходило на базе этого общего закона. Начиная со второй половины XIX столетия измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа. Если инди­видуальная изменчивость некоторого свойства есть следствие действия мно­жества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения. Это и есть закон нормального распределения. Нормальное распределение как стандарт. Каждому психологическому (или шире – биосоциальному) свойству соот­ветствует свое распределение в генеральной совокупности. Чаще всего оно является нормальным и характеризуется своими параметрами: средним (М) и стандартным отклонением (σ). Только эти два значения полностью определяют форму кривой нормального распределения. Среднее задает положение кривой на числовой оси и выступает как некоторая исходная, нормативная величина измерения. Стандар­тное отклонение задает ширину этой кривой, зависит от единиц измерения и выступает как масштаб измерения.

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ

Упражнение

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ Рассмотрим свойства нормального распределения. 1) Единицей измерения единичного нормального распределения являет­ся стандартное отклонение. 2) Кривая приближается к оси Z по краям асимптотически – никогда не касаясь ее. 3) Кривая симметрична относительно М= 0. Ее асимметрия и эксцесс рав­ны нулю. 4) Кривая имеет характерный изгиб: точка перегиба лежит точно на рас­стоянии в одну о от М. 5) Площадь между кривой и осью Z равна 1. Последнее свойство объясняет название «единичное нормальное распреде­ление» и имеет исключительно важное значение. Благодаря этому свойству площадь под кривой интерпретируется как вероятность, или относительная частота. Действительно, вся площадь под кривой соответствует вероятности того, что признак примет любое значение из всего диапазона его изменчиво­сти (от – ∞ до + ∞). Площадь под единичной нормальной кривой слева или справа от нулевой точки равна 0,5. Это соответствует тому, что половина ге­неральной совокупности имеет значение признака больше 0, а половина — меньше 0. Относительная частота встречаемости в генеральной совокупнос­ти значений признака в диапазоне от z1 до z2 равна площади под кривой, ле­жащей между соответствующими точками. Отметим еще раз, что любое нор­мальное распределение может быть сведено к единичному нормальному распределению путем z-преобразования.

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ Полезно помнить, что для любого нормального распределения существу­ют следующие соответствия между диапазонами значений и площадью под кривой: М±σ соответствует 68,26% площади; М±2σ соответствует 95,44% площади; М±3σ соответствует 99,72% площади. Если распределение является нормальным, то: 90% всех случаев располагается в диапазоне значений М±1,64σ; 95% всех случаев располагается в диапазоне значений М±1,96σ; 99% всех случаев располагается в диапазоне значений М±2,58σ. Единичное нормальное распределение устанавливает четкую взаимосвязь стандартного отклонения и относительного количества случаев в генераль­ной совокупности для любого нормального распределения. Существуют правила перевода (специальная таблица, например), позволяющая определять площадь под кривой справа от любого положительного z. Пользуясь ею, можно определить вероятность встречаемости значений признака из любого диапазона. Это широко используется при интерпретации данных тестирования.

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ В ПСИХОЛОГИИ Несмотря на исходный постулат, в соответствии с которым свойства в ге­неральной совокупности имеют нормальное распределение, реальные дан­ные, полученные на выборке, не всегда распределены нормально. Более того, разработано множество методов, позволяющих анализировать данные без всякого предположения о характере их распределения как в выборке, так и в генеральной совокупности. Тем не менее, существуют по крайней мере три важных аспекта применения нормального распределения в психологии: Разработка тестовых шкал. Проверка нормальности выборочного распределения для принятия ре­шения о том, в какой шкале измерен признак – в метрической или по­рядковой. Статистическая проверка гипотез, в частности – при определении риска принятия неверного решения.

Разработка тестовых шкал Разработка тестовых шкал. Тестовые шкалы разрабатываются для того, чтобы оценить индивидуаль­ный результат тестирования путем сопоставления его с тестовыми нормами, полученными на выборке стандартизации. Выборка стандартизации специаль­но формируется для разработки тестовой шкалы — она должна быть репре­зентативна генеральной совокупности, для которой планируется применять данный тест. Впоследствии при тестировании предполагается, что и тестиру­емый, и выборка стандартизации принадлежат одной и той же генеральной совокупности. Исходным принципом при разработке тестовой шкалы является предпо­ложение о том, что измеряемое свойство распределено в генеральной сово­купности в соответствии с нормальным законом. Соответственно, измерение в тестовой шкале данного свойства на выборке стандартизации также должно обеспечивать нормальное распределение. Если это так, то тестовая шкала является метрической — точнее, равных интервалов. Если это не так, то свой­ство удалось отразить в лучшем случае — в шкале порядка. Естественно, что большинство стандартных тестовых шкал являются метрическими, что по­зволяет более детально интерпретировать результаты тестирования — с уче­том свойств нормального распределения — и корректно применять любые методы статистического анализа. Таким образом, основная проблема стандар­тизации теста заключается в разработке такой шкалы, в которой распределе­ние тестовых показателей на выборке стандартизации соответствовало бы нормальному распределению.

Разработка тестовых шкал Исходные тестовые оценки — это количество ответов на те или иные вопросы теста, время или количество решенных задач и т. д. Они еще называют­ся первичными, или «сырыми» оценками. Итогом стандартизации являются тестовые нормы – таблица пересчета «сырых» оценок в стандартные тестовые шкалы. Существует множество стандартных тестовых шкал, основное назначение которых — представление индивидуальных результатов тестирования в удоб­ном для интерпретации виде. Некоторые из этих шкал представлены на рис. Общим для них является соответствие нормальному распределению, а различаются они только двумя показателями: средним значением и масштабом (стандартным отклонением σ), определяющим дробность шкалы.

Некоторые из известных равноинтервальных шкал в психологии

Последовательность стандартизации – разработки тестовых норм Общая последовательность стандартизации (разработки тестовых норм — таб­лицы пересчета «сырых» оценок в стандартные тестовые) состоит в следующем: определяется генеральная совокупность, для которой разрабатывается методика и формируется репрезентативная выборка стандартизации; по результатам применения первичного варианта теста строится распределение «сырых» оценок; проверяют соответствие полученного распределения нормальному за­кону; если распределение «сырых» оценок соответствует нормальному, про­изводится линейная стандартизация; если распределение «сырых» оценок не соответствует нормальному, то возможны два варианта: перед линейной стандартизацией производят эмпирическую норма­лизацию; проводят нелинейную нормализацию. Более подробно примеры и варианты стандартизации будут рассмотрены на лабораторных занятиях, а также упражнения на стандартизацию и тестовые шкалы.

Вопросы для проработки и самостоятельного изучения 1. Первичные описательные статистики. Меры центральной тенденции: среднее арифметическое. Преимущества и недостатки. Понятие моды как наиболее часто встречаемого признака в выборке. Правила нахождения моды для разных случаев. Бимодальные и мультимодальные выборки. Медиана как значение, делящее упорядоченное множество пополам. 2. Меры изменчивости. Разброс выборки. Дисперсия как характеристика отклонения от среднего. Стандартное отклонение. Стандартная ошибка для количественных признаков и долей. Квантили распределения (процентили, квартили). 3. Понятие нормального распределения и его параметры: среднее арифметическое и стандартное отклонение. Идеальная кривая нормального распределения К. Гаусса. Свойства кривой. Совпадение значений среднего арифметического, моды и медианы. Ассиметричные распределения: левосторонние, правосторонние. 4. Разработка тестовых норм. Процедура стандартизации. Различные шкалы, применяемые в тестах в результате стандартизации. Их связь с нормальным распределением.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ Формулирование гипотез систематизирует предположения иссле­дователя и представляет их в четком и лаконичном виде. Статистические гипотезы подразделяются на нулевые и альтернативные, направленные и ненаправленные. Нулевая гипотеза – это гипотеза об отсутствии различий или значимых связей (что одно и то же, ниже мы поясним это). Она обозначается как H0 и называется нулевой потому, что содержит число 0: X1 – Х2 = 0, где Х1, X2 – сопоставляемые значения признаков. Нулевая гипотеза – это то, что мы хо­тим опровергнуть, если перед нами стоит задача доказать значимость различий. Альтернативная гипотеза – это гипотеза о значимости различий. Она обозначается как Н1. Чаще в исследованиях требуется доказать наличие статистически значимых различий. Однако, бывают задачи, когда желательно доказать как раз отсутствие статистической значимости различий, то есть подтвердить нулевую гипотезу, – например, если исследователю нужно убедиться, что разные испытуемые получают хотя и различные, но уравновешенные по трудности задания, или что экспериментальная и контрольная выборки не различаются между собой по каким-то характеристикам помимо исследуемого фактора. Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными, а также с двусторонней или односторонней критической областью (последнее мы поясним ниже).

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ Статистические критерии. Статистический критерий – это решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью. Статистические критерии обозначают также метод расчета опре­деленного числа и само это число. Критерий включает в себя: формулу расчета эмпирического значения критерия по выборочным статистикам; правило (формулу) определения числа степеней свободы; теоретическое распределение для данного числа степеней свободы; правило соотнесения эмпирического значения критерия с теоретическим распределением для определения того, что Н0 верна. Когда говорят, что статистическая значимость различий определялась по критерию χ2, то имеется в виду, что использовали метод χ2 для расчета определенного числа. Когда говорят, что χ2=42,676, то имеем в виду опре­деленное число, рассчитанное по методу χ2. Это число обозначается как эмпирическое значение критерия.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ В большинстве случаев для того, чтобы мы признали различия статистически значимыми, необходимо, чтобы эмпирическое значение критерия пре­вышало критическое, хотя есть критерии (например, критерий Манна-Уитни или критерий знаков), в которых мы должны придерживаться противоположного правила. В некоторых случаях расчетная формула критерия включает в се­бя количество наблюдений в исследуемой выборке, обозначаемое как n. В этом случае эмпирическое значение критерия одновременно является тестом для проверки статистических гипотез. По специальной таблице вручную мы определяем, какому уровню статистической значимости различий соответствует данная эмпирическая величина. Примером такого крите­рия является t-критерий Стьюдента. Или компьютерный пакет выдает уровень статистической значимости. В большинстве случаев, однако, одно и то же эмпирическое зна­чение критерия может оказаться значимым или незначимым в зависи­мости от количества наблюдений в исследуемой выборке (n) или от так называемого количества степеней свободы, которое обозначается как ν или как df. Для каждого случая определение количества степеней свободы имеет свою специфику, поэтому каждая формула для расчета эмпирического значения критерия обязательно сопровождается правилом (формулой) для определения числа степеней свободы. Зная n и/или число степеней свободы, мы по специальным таб­лицам можем определить критические значения критерия и сопоставить с ними полученное эмпирическое значение.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ Критерии делятся на параметрические и непараметрические. Параметрические критерии включают в формулу расчета параметры распределения, то есть средние и дисперсии (t-критерий Стьюдента, критерий F Фишера и др.) Непараметрические критерии не включают в формулу расчета параметров распределе­ния и основаны на оперировании частотами или рангами (критерий U Манна-Уитни, критерий Т Вилкоксона и др.). Параметрические критерии могут более мощными; чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. С интервальной шкалой есть определенные проблемы. Лишь с некоторой натяжкой мы можем считать данные, представленные не в стандартизованных оценках, как интервальные. Кроме того, проверка распределения на нормальность требует достаточно сложных расчетов, результат кото­рых заранее неизвестен. Может оказаться, что рас­пределение признака отличается от нормального, и нам так или иначе все равно придется обратиться к непараметрическим критериям. Непараметрические критерии лишены всех этих ограничений, и не требуют таких длительных и сложных расчетов. По сравнению с пара­метрическими критериями они ограничены лишь в одном - с их помо­щью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту задачу может решить только дисперсионный двухфакторный анализ.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ Уровни статистической значимости. Уровень значимости – это вероятность того, что исследователь счел разли­чия существенными, а они на самом деле случайны. Когда мы указываем, что различия достоверны на 5%-ом уровне значимости, или при р<0,05, то мы имеем виду, что вероятность того, что они все-таки недостоверны, составляет 0,05 (или 0,05·100%=5%). Когда мы указываем, что различия достоверны на 1%-ом уровне значимости, или при р<0,01, то мы имеем в виду, что вероятность того, что они все-таки недостоверны, составляет 0,01. Уровень значимости - это вероятность отклонения нулевой гипотезы, в то время как она верна. Ошибка, состоящая в том, что мы отклонили нулевую гипотезу, в то время как она верна, называется ошибкой 1 рода. Если вероятность ошибки - это α, то вероятность правильного решения: 1–α. Чем меньше α, тем больше вероятность правильного решения.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ Исторически сложилось так, что в психологии принято считать низшим уровнем статистической значимости 5%-ый уровень (р<0,05): достаточным - 1%-ый уровень (р<0,01) и высшим 0,1%-ый уровень (р<0,001), поэтому в таблицах критических значений обычно приводят­ся значения критериев, соответствующих уровням статистической зна­чимости р<0,05 и р<0,01, иногда – р<0,001. Для некоторых критериев в таблицах указан точный уровень значимости их разных эмпирических значении. До тех пор, однако, пока уровень статистической значимости не достигнет р=0,05, мы еще не имеем права отклонить нулевую гипотезу. Правило отклонения H0 и принятия Н1. Если эмпирическое значение критерия равняется критическому значе­нию, соответствующему р<0,05 или превышает его, то H0 отклоняет­ся, но мы еще не можем определенно принять H1. Если эмпирическое значение критерия равняется критическому значе­нию, соответствующему р<0,01 или превышает его, то Н0 отклоняется и принимается H1. Исключения: критерий знаков G, критерий Т Вилкоксона и критерий U Манна-Уитни. Для них устанавливаются обратные соотношения. Практически, однако, исследователь может считать достоверными уже те различия, которые не попадают в зону незначимости, заявив, что они статистически значимы при р<0,05, или указав точный уровень значимости полученного эмпирического значения критерия, например: р=0,02.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ Мощность критерия – это его способность выявлять различия, если они есть. Иными словами, это его способность отклонить нулевую гипотезу об отсутствии различий, если она неверна. Ошибка, состоящая в том, что мы приняли нулевую гипотезу, в то время как она неверна, называется ошибкой II рода. Вероятность такой ошибки обозначается как β. Мощность крите­рия - это его способность не допустить ошибку II рода, поэтому: Мощность=1–β Мощность критерия определяется эмпирическим путем. Одни и те же задачи могут быть решены с помощью разных критериев, при этом обнаруживается, что некоторые критерии позволяют выявить раз­личия там, где другие оказываются неспособными это сделать, или вы­являют более высокий уровень значимости различий. Возникает вопрос: а зачем же тогда использовать менее мощные критерии? Дело в том, что основанием, для выбора критерия может быть не только мощность, но и другие его характеристики, а именно: простота; более широкий диапазон использования (например, по отношению к данным, определенным по номинативной шкале, или по отношению к большим n); применимость по отношению к неравным по объему выборкам; большая информативность результатов.

Статистическая мощность Величина мощности при проверке статистической гипотезы зависит от следующих факторов: величины уровня значимости, обозначаемого греческой буквой альфа, на основании которого принимается решение об отвержении или принятии альтернативной гипотезы; величины эффекта (то есть разности между сравниваемыми средними); размера выборки, необходимой для подтверждения статистической гипотезы.

Размер эффекта Величина эффекта определяет вероятность совершения ошибки второго рода. Коэффициент величины эффекта называется мерой эффекта d. Был введён в употребление Дж. Коэном и вычисляется как отношения разности между сравниваемыми средними к стандартному отклонению. Размер выборки, необходимой для подтверждения статистической гипотезы, влияет на статистическую мощность, так как с увеличением выборки уменьшается стандартная ошибка, а следовательно, увеличивается мощность. Понятия «размер эффекта», которым должен руководствоваться исследователь помимо собственно статистической значимости, будут рассмотрены на лабораторных занятиях, по отношению к различным типам переменных и характеристиках связи или различия.

Задачи статистического сравнения двух средних или двух частот Возможный алгоритм действий

Планирование эксперимента: расчет объема выборок

Обоснование задачи сопоставления и сравнения Очень часто перед исследователем в психологии стоит задача вы­явления различии между двумя, тремя и более выборками испытуемых. Это может быть, например, задача определения психологических осо­бенностей хронически больных детей по сравнению со здоровыми, юных правонарушителей по сравнению с законопослушными сверстни­ками или различий между работниками государственных предприятии и частных фирм, между людьми разной национальности или разной куль­туры и, наконец, между людьми равного возраста в методе «поперечных срезов». Сопоставление уровневых показателей в разных выборках может быть необходимой частью комплексных диагностических, учебных, психокоррекционных и иных программ. Оно помогает нам обратить внимание на те особенности обследованных выборок, которые должны быть учтены и использованы при адаптации программ к данной группе процессе их конкретного воплощения.

Обоснование задачи статистической значимости сдвига в значениях исследуемого признака В психологических исследованиях часто бывает важно доказать, что в результате действия каких-либо факторов произошли достоверные изменения (сдвиги) в измеряемых показателях. Сопоставление показателей, полученных у одних и тех же испытуемых по одним и тем же методикам, но в разное время, определяет временной сдвиг. Сопоставление показателей, полученных по одним и тем же методикам, но в разных условиях измерения (например, «покоя» и «стресса»), дает нам ситуационный сдвиг. Условия измерения могут изменяться не только реально, но и умозрительно. Например, мы мо­жем попросить испытуемого "представить себе", что он оказался в других условиях измерения: в будущем, в позиции других людей, кото­рые оценивают его как бы со стороны, в состоянии разгневанного отца и т. п. Сопоставляя показатели, измеренные в обычных и воображае­мых условиях, мы получаем умозрительный сдвиг. Мы можем создать специальные экспериментальные условия, предположительно влияющие на те или иные показатели, и сопоставить замеры, произведенные до и после экспериментального воздействия. Если сдвиги окажутся статистически достоверными, это позволит нам утверждать, что экспериментальные воздействия были существенными, или эффективными.

Обоснование задачи статистической значимости сдвига в значениях исследуемого признака Например, мы можем сделать вывод о том, что данная програм­ма тренинга действительно способствует развитию уверенности, или что данный способ внушающего воздействия влияет на изменение отноше­ния испытуемых к той или иной проблеме, или что психодраматическая замена ролей подтверждает постулат Дж.Л. Морено о сближении по­зиций спорщиков после того, как им пришлось играть роль своего оп­понента и т.п. Во всех этих случаях мы говорим о сдвиге под влиянием контро­лируемых или не контролируемых воздействий. Можно рассмотреть еще особую категорию структурных сдвигов. Так, мы можем сопоставлять между собой разные показатели одних и тех же испытуемых, если они измерены в одних и тех же единицах, по одной и той же шкале. Например, мы можем исследовать перепад ме­жду вербальным и невербальным интеллектом, измеренными по мето­дике Д. Векслера, или сопоставлять экспертные оценки эмпатичности и наблюдательности, измеренные по одинаковой 10-балльной шкале, или время решения двух задач, измеренное в секундах, или экзаменацион­ную успешность по разным дисциплинам и т.п. Для установления достоверности сдвигов в значениях признака в связанных выборках (чаще всего, как указано выше, это те же самые испытуемые) используются специальные статистические критерии для связанных выборок.

ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ.

ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ. Функциональные связи, подобные изображенным на рис. выше, являются идеализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр. В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Будем говорить, что между двумя признаками Х и Y существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака Y, и наоборот. Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.

ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ. Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной. Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной. В ряде случаев необходимо определить связь между двумя признаками, установить характер зависимости (прямая или обратная), количественно выразить достоверность связи. Для решения этих задач вычисляют коэффициент корреляции r. Величина коэффициента корреляции лежит в пределах от –1 до +1. Если коэффициент корреляции близок по модулю единице, то между изменением величины Х и Y существует линейно пропорциональная зависимость. Если r>0, то с ростом величины X величина Y также в среднем растет. Если r<0, то с ростом величины X величина Y в среднем убывает. Если коэффициент корреляции по модулю близок нулю, то между величинами Х и Y отсутствует линейная связь. Таким образом, коэффициент корреляции – важный показатель, показывающий взаимосвязь между двумя наборами данных. Отрицательное значение указывают на обратную корреляцию, положительное – на прямую. Чем ближе к 1 значение r, тем вероятнее наличие связи между показателями.

ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ.

ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ. Две эти классификации не совпадают. Первая ориентирована только на величину коэффициента корреляции, а вторая определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньшей величины коэффициента корреляции оказывается доста­точно, чтобы корреляция была признана достоверной. В результате при малом объеме выборки может оказаться так, что сильная корреляция окажется недостоверной. В то же время при больших объемах выборки даже слабая корреляция может оказаться достоверной. Обычно принято ориентироваться на вторую классификацию, по­скольку она учитывает объем выборки. Вместе с тем, необходимо пом­нить, что сильная, или высокая, корреляция – это корреляция с коэффи­циентом r ≥ 0,70, а не просто корреляция высокого уровня значимости.

Некоторые критерии для сравнения выборок Более подробно будут рассмотрены на лабораторных работах. 1. Критерии проверки на нормальность: критерий «хи-квадрат» Пирсона χ2 ,тест Шапиро-Уилка 2. Параметрические критерии для независимых и зависимых выборок – критерии Стьюдента, дисперсионный анализ, апостериорные критерии для попарных сравнений (например, Шеффе, Даннета – при сравнениях с контрольной группой). 3. Непараметрические критерии для независимых выборок (Манна-Уитни), зависимых (Вилкоксона), критерий Крускала-Уоллиса для независимых и Фридмана для зависимых выборок, апостериорные критерии (например, Данна). 4. Параметрический Критерий Фишера для сравнений дисперсий в двух выборках. 5. Критерии хи-квадрат Пирсона, Колмогорова-Смирнова, биномиальный критерий для выявления согласия распределений.

Некоторые критерии для сравнения выборок 6. Многофункциональные критерии «Угловое преобразование Фишера», «Хи-квадрат Фишера» для независимых выборок, критерий Мак-Немара для зависимых выборок – для сравнения категориальных данных. 7. Методы корреляционного анализа: коэффициент корреляции Пирсона (параметрический метод); Кендалла, Спирмена, бисериальная корреляция (непараметрические методы). 8. Критерии тенденций Пейджа, Джонкира; анализ «выживаемости», и еще очень-очень много разных критериев, лишь некоторые из них мы с Вами будем разбирать, но и их достаточно для 95% задач на сравнения, с которыми Вы столкнетесь. Для остальных задач на сравнения существуют многомерные методы.

Вопросы для проработки и самостоятельного изучения Понятие статистической гипотезы. Сущность проверки статистической гипотезы – установить, согласуются ли экспериментальные результаты и выдвинутая гипотеза; допустимо ли отнести расхождение между ними за счет случайных величин. Нулевая гипотеза. Понятие уровня статистической значимости как вероятности ошибки при принятии решения об отклонении нулевой гипотезы. Уровни статистической значимости. Этапы принятия статистической гипотезы (решения). Ошибка второго рода. Мощность критерия. Статистическая и содержательная (психологическая, клиническая) значимость.

Многомерные методы математической статистики в психологии Многомерные методы необходимы для одновременного учета многих переменных (признаков) в результирующий или для классификации признаков или случаев, а также для понижения размерности (укрупнения признаков) – для лучшего понимания закономерностей, лежащих в основе явлений. А также для построения эмпирических моделей явлений, их количественного описания на основе наблюденных данных. Причем, важной составляющей любого математико-статистического метода является точность или, иначе говоря, ошибка, то есть величина, которая характеризует то, насколько точно или полно модель описывает исследуемое явление, характеристики которого мы наблюдаем на опыте. Среди наиболее часто применяемых на практике многомерных математико-статистических методов в психологии следует выделить: Кластерный анализ Факторный анализ Множественный регрессионный анализ

Кластерный анализ: описание метода В основе кластерного анализа лежит идея классификации объектов и выделения среди этого множества групп (кластеров) объектов, сходных по замеренным параметрам. Кластерный анализ – это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы. В результате работы с процедурами образуются «кластеры» или группы очень похожих объектов Одна из ключевых особенностей кластерного анализа заключается в том, что исследователь до начала кластеризации не имеет четких предположений о том, какие именно группы объектов будут выделены в ходе проведения процедуры. Сама процедура кластеризации предполагает, что в одной группу будут попадать объекты, наиболее сходные по своим характеристикам. Например, Кластерный анализ в психосемантике позволяет решить одну из основных исследовательских задач – необходимость реконструировать категориальную структуру сознания испытуемого для исследуемой области без выдвижения предварительных предположений о том, в какие именно группы и каким образом будут объединяться объекты или категории. При проведении кластерного анализа в психосемантических исследованиях используется группа методов, объединенных названием иерахических (Hierarchical Cluster Analysis).

Кластерный анализ: описание метода При проведении кластерного анализа и последующей интерпретации полученных данных нужно учитывать следующие его особенности: 1. Многие методы кластерного анализа – довольно простые процедуры, которые, как правило, не имеют достаточного статистического обоснования. Это не дает возможности утверждать о статистической достоверности полученных решений. 2. Разные кластерные методы могут порождать и порождают различные решения для одних и тех же данных. Что, в свою очередь, может приводить к разным выводам при интерпретации данных 3. Цель кластерного анализа заключается в поиске существующих структур. В то же время его действие состоит в привнесении структуры в анализируемые данные, т.е. методы кластеризации необходимы для обнаружения структуры в данных, которую нелегко найти при визуальном обследовании или с помощью экспертов. Другими словами, в результате кластерного анализа мы получаем некое представление о том, как именно могли бы объединяться объекты в группы. Но в большой степени на это влияет выбор метода кластеризации и способа расчета матрицы расстояний между объектами. Это означает, что исследователь должен достаточно критично отнестись к результатам, полученным в результате кластеризации. Оптимальным решением в данном случае может быть получение нескольких решений (кластерных деревьев) разными способами кластеризации, и обсуждение тех кластеров, которые устойчиво встречаются в нескольких вариантах решений.

Кластерный анализ: описание метода Наиболее часто кластерный анализ используется для обработки данных, полученных методами классификации, репертуарных решеток и семантического дифференциала. При использовании метода классификации мы получаем результаты, показывающие, как именно испытуемые классифицировали те или иные объекты. Если данные получены на одном испытуемом, то сразу можно получить представление о том, по каким именно группам испытуемый распределил объекты. В случае, когда есть данные, собранные на выборке испытуемых, то для обработки общегрупповой матрицы используется кластерный анализ, так как визуальная оценка данных в данном случае неудобна, а иногда и просто не выполнима. Чаще всего кластерный анализ используется лля обработки данных, полученных с помощью репертуарных решеток Келли. В данном случае предполагается, что близость объектов в кластерном дереве сопряжена со сходством оценок объектов. А значит, объекты, попадающие в один кластер, могут быть проинтерпретированы как похожие, сходные по своим характеристикам. При обработке данных, полученных с помощью семантического дифференциала, чаще всего используются такие методы многомерной обработки данных как факторный анализ и многомерное шкалирование. Однако, исследователь также может использовать и кластерный анализ, если хочет проверить, в какие группы могут объединяться объекты семантического дифференциала. Для интерпретации используется та же самая логика, что и для репертуарных решеток Келли.

Обработка данных методом кластерного анализа Последовательность проведения кластерного анализа: 1. Отбор объектов для кластеризации. Объектами могут быть, в зависимости от цели исследования: а) испытуемые; б) объекты, которые оцениваются испытуемыми; в) признаки, измеренные на выборке испытуемых. 2. Определение множества переменных, по которым будут различаться объекты кластеризации. 3. Определение меры различия между объектами кластеризации. 4. Выбор и применение метода классификации для создания групп сходных объектов. 5. Проверка достоверности разбиения на классы. Рассмотрим каждый из этапов более подробно

Последовательность проведения кластерного анализа: 1. Отбор объектов для кластеризации. На данном этапе определяется, какая именно совокупность объектов будет распределяться на кластеры. При обработке результатов, полученных методом репертуарных решеток, как правило, в качестве кластеризуемых объектов выступает список репертуарных ролей. Реже, в качестве объектов кластеризации выступают полученные дескрипторы. В семантическом дифференциале объектами кластеризации выступают объекты оценивания. Для метода классификации кластеризации подвергаются собственно классифицируемые объекты. 2. Определение множества переменных, по которым будут различаться объекты кластеризации. При использовании семантических методов таким множеством переменных выступают дескрипторы (конструкты). 3. Определение меры различия между объектами кластеризации. Кластерный анализ проводится на матрице расстояний между объектами. Поэтому для исследователя важно определиться с тем, какой мерой расстояния (сходства) он будет пользоваться. Чаще всего используются две из них: - евклидово расстояние (Euclidian distance); - коэффициент корреляции Пирсона. Евклидово расстояние легко представляется как кратчайшее расстояние между двумя точками (объектами) в пространстве двух, трех и более координат. Наиболее подходит для метрических данных (в шкале интервалов или отношений).

Последовательность проведения кластерного анализа: Вариант графического представления евклидова расстояния в трехмерном пространстве показан на рисунке.

Последовательность проведения кластерного анализа: Коэффициент корреляции – двухмерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных. Коэффициент корреляции Пирсона является мерой сходства объектов, применяется для изучения взаимосвязи переменных, измеренных на одной и тоже выборке Формула коэффициента корреляции выглядит следующим образом: Данный способ построения матрицы расстояний хорош также тем, что позволяет определить статистически достоверный уровень значимой связи между объектами в кластерном дереве. Для этого мы можем воспользоваться таблицей критических значений коэффициента корреляции Пирсона, которая, как правило, есть в любом учебнике по математической статистике. В таблице мы выбираем значение корреляции Пирсона, соответствующее количеству дескрипторов в матрице, на основе которой было построено кластерное дерево. Так, для дерева, построенного на основе матрицы, содержащей 10 дескрипторов, критическое значение коэффициента корреляции Пирсона составляет 0,632 (p≤0,05). Так как в мере расстояния используется формула 1 – Pearson r, то критическое значение коэффициента корреляции вычитается из единицы: 1 – 0,632=0,368

Последовательность проведения кластерного анализа: Таким образом, кластеры, уровень связи в которых от 0 до 0,368, будут интерпретироваться как сильная связь, от 0,368 до 1,632 – как слабая связь, а от 1,632 до 2 – как сильное противопоставление. Другими словами, уровень связи ближе к 0 либо к 2 – связь между объектами в кластере (кластерами) будет интерпретироваться как более сильная. Уровень связи близкий к 1 – интерпретируется как отсутствие связи между объектами в кластере, либо между кластерами. Аналогично можно рассчитать статистически значимую связь между объектами при другой размерности матрицы.

Последовательность проведения кластерного анализа: 4. Выбор и применение метода классификации для создания групп сходных объектов. В данном случае речь идет о выборе алгоритма кластеризации и построения кластерного дерева. Чаще всего используются следующие методы: 1. Метод одиночной связи (Single Linkage). Алгоритм начинается с поиска двух наиболее близких объектов, пара которых образует первичный кластер. Каждый последующий объект присоединяется к тому кластеру, к одному из объектов которого он ближе. Метод имеет тенденцию образовывать небольшое число крупных кластеров. 2. Метод полной связи (Complete Linkage). Новый объект присоединяется к тому кластеру, самый далекий элемент которого находится ближе к новому объекту, чем самые далекие элементы других кластеров. При использовании этого метода наблюдается тенденция к выделению большого числа компактных кластеров, состоящих из наиболее похожих элементов. 3. Метод средней связи (Average Linkage). На каждом шаге вычисляется среднее арифметическое расстояние между каждым объектом из одного кластера и каждым объектом из другого кластера. По своему принципу этот метод должен давать более точные результаты классификации, чем остальные методы. 4. Метод Варда (Ward’s method). Этот метод построен таким образом, чтобы оптимизировать минимальную дисперсию внутри классов. Основная идея метода в том, чтобы усилить различия между классами, минимизируя расстояния между ближними объектами и усиливая расстояние между дальними. Метод имеет тенденцию к нахождению (или созданию) кластеров приблизительно равных размеров. Этот метод довольно широко используется в социальных науках.

Последовательность проведения кластерного анализа в статистическом пакете Statistica. В качестве примера описывается пример обработки данных, полученных методом репертуарных решеток. Результаты репертуарных решеток удобно сначала представлять в Excel. Например, как это сделано на рисунке.

Последовательность проведения кластерного анализа в статистическом пакете Statistica. Данные (только численные данные) переносятся в программу Statisitica:

Последовательность проведения кластерного анализа в статистическом пакете Statistica.

Последовательность проведения кластерного анализа в статистическом пакете Statistica.

Последовательность проведения кластерного анализа в статистическом пакете Statistica.

Последовательность проведения кластерного анализа в статистическом пакете Statistica.

Последовательность проведения кластерного анализа в статистическом пакете Statistica.

Интерпретация результатов кластерного анализа Принципы интерпретации данных: 1. Основная задача кластерного анализа – это объединение объектов в кластеры (группы) по какому-то определенному принципу таким образом, чтобы в каждый из кластеров попадали наиболее сходные по характеристикам объекты. Применительно к репертуарным решеткам Келли или семантическому дифференциалу это означает, что в один кластер будут попадать объекты (роли), оцененные испытуемым схожим образом. И, напротив, в различающиеся кластеры будут попадать объекты (роли), которым испытуемый давал разные оценки по дескрипторам или конструктам. 2. Интерпретация в данном случае строится на том, что мы описываем, какие именно объекты или роли попадают в один кластер, примыкающие кластеры или в различающиеся кластеры, и реконструируем принцип, которым неявно руководствовался испытуемый при оценке объектов (ролей). 3. Для репертуарных решеток Келли важным моментом при интерпретации данных выступает наличие в списке ролей так называемых «маркерных» ролей. Их присутствие с другими ролями в кластере позволяет дать содержательную оценочную интерпретацию немаркированным ролям (таким как «Я», «Я через 15 лет», «Подруга/Друг» и т.д.).

Интерпретация результатов кластерного анализа Пример интерпретации кластерного дерева. Данные были получены с помощью метода репертуарных решеток Келли. Список репертуарных ролей выглядел следующим образом: 1. Я; 2. Мать; 3. Отец; 4. Возлюбленный; 5. Подруга; 6. Бывший возлюбленный (возлюбленная), 7. Бывшая подруга, 8. Человек, который мне не нравится, 9. Человек, которому я не нравлюсь, 10. Успешный человек, 11. Вызывающий жалость, 12. Комфортный начальник, 13. Некомфортный начальник, 14. Неудачник, 15. Авторитетный человек, 16. Человек, чье мнение безразлично. 17. Счастливый человек, 18. Я через 15 лет.

Интерпретация результатов кластерного анализа При анализе кластерного дерева можно условно выделить пять основных кластеров. Помимо них, отдельно выделяется роль «Отец». Вероятно, это связано с тем, что у испытуемой неполная семья, поэтому образ отца практически не пересекается с другими окружающими ее людьми, так как мало его знает и затрудняется оценить по шкалам. Также отдельно от групп стоит «Бывшая подруга», это значит, что она значительно отличается от самой испытуемой и ее настоящей подруги по большинству конструктов. Собственные оценки и оценки подруги испытуемой похожи и образуют первый кластер. Судя по этому, можно сказать, что испытуемая выбирает близких друзей по сходству в выделенных конструктах с собой, что, в принципе, и является основой дружеских отношений. Следующий крупный кластер объединяет в себе две подгруппы: первая включает роли «Мама», «Авторитетный человек», «Счастливый человек» и «Я через 15 лет»; вторая – «Возлюбленный» и «Бывший возлюбленный». Судя по первой подгруппе можно сделать вывод о том, что испытуемая ассоциирует «Маму» с ролью «Счастливый человек», считается с ее мнением и равняется на нее, т.к. свой образ в перспективе она наделяет теми же качествами, которые видит в маме. Можно сделать вывод о том, что мама является для испытуемой источником Я-идеального, характеристики которого она видит и в «Авторитетном человеке», и в «Счастливом человеке», и в образе себя, к которому стремится в будущем. Вторая подгруппа в этом кластере объединяет роли «Бывший возлюбленный» и «Возлюбленный». Это указывает на то, что испытуемая выбирает определенный тип мужчин в романтических отношениях. Связь этих двух подгрупп в кластере может говорить о том, что испытуемая видит в перспективе свое сходство с любимым человеком по некоторым конструктам и, в целом, ассоциирует свое будущее с любовными отношениями.

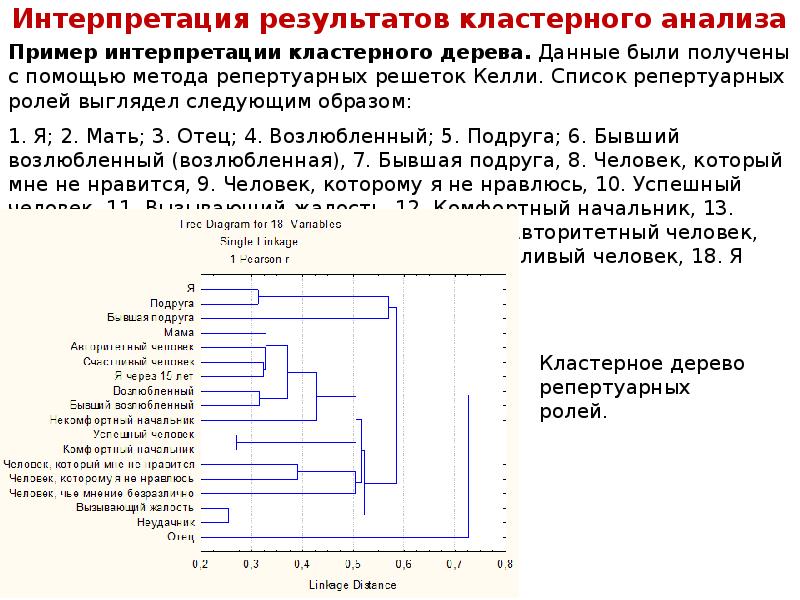
Интерпретация результатов кластерного анализа Следующий кластер объединяет роли «Успешный человек» и «Комфортный начальник». Можно предположить, что в представлении испытуемой успешный человек – это человек, реализовавшийся, в первую очередь, в сфере работы и как организатор, т.е. обладающий теми же качествами, что и начальник, под руководством которого комфортно работать. Четвертый кластер составляют «Человек, который мне не нравится» и «Человек, которому не нравлюсь я». Их объединение говорит об однозначной негативной оценке обоих и, возможно, представляет собой такой обобщенный образ «плохого» человека, характеризуемый оценками, близкими скорее к контрасту, нежели к конструкту. Последний кластер образуют «Вызывающий жалость» и «Неудачник», которые имеют самое сильное сходство среди всех ролей. Этот кластер автономен по отношению к другим, значит, испытуемая не ассоциирует ни себя, ни свое окружение с негативными качествами, проявляющимися в этих ролях. В целом, стоит обратить внимание на то, что роль «Я», описывающая испытуемую в актуальный момент, и роль «Я через 15 лет» находятся в разных кластерах и имеют слабую связь. Это может говорить о том, что разрыв между Я-реальным и Я-идеальным достаточно большой, что может являться следствием неадекватной самооценки, поэтому испытуемая может не представлять реальных способов продвижения к Я-идеальному, как, собственно, и к образу «Счастливого человека», также находящегося во втором кластере. Кроме того, свое будущее испытуемая ассоциирует скорее с семьей, чем с работой, т.к. обе роли, описывающие руководителя («Комфортный начальник», «Некомфортный начальник») находятся не в одном кластере с ролью «Я через 15 лет». Однако существует небольшая связь второго кластера с ролью «Некомфортного начальника». Это может говорить о том, что испытуемая не видит свое будущее на организаторском поприще, т.к. ассоциирует образ «Я через 15 лет» с «Некомфортным начальником». Однако, эта связь не дает достаточных оснований делать такой вывод и может быть объяснена схожими оценками этих двух ролей лишь по тем конструктам, которые не значимы в профессиональной деятельности.

Описание метода факторного анализа Факторный анализ является статистическим методом, используемым при обработке больших массивов экспериментальных данных. Под факторным анализом понимают совокупность статистических процедур, направленных на выделение из заданного множества переменных подмножеств переменных, тесно связанных (коррелирующих) между собой Главными целями факторного анализа являются: (1) сокращение числа переменных (редукция данных) и (2) определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод редукции данных или как метод классификации данных. Важное отличие факторного анализа от прочих методов анализа данных заключается в том, что его нельзя применить для обработки первичных, или как говорят, «сырых» экспериментальных данных, полученных непосредственно при обследовании испытуемых. Другими словами, факторному анализу подвергают корреляционные матрицы, построенные между переменными на основе коэффициента корреляции Пирсона.

Психологические задачи факторного анализа. Факторный анализ в психологии используется, во-первых, для исследований структуры личности, темперамента и способностей. Использование факторного анализа в этих сферах основано на допущении, согласно которому наблюдаемые и доступные для прямого измерения показатели являются лишь косвенными и/или частными внешними проявлениями более широких характеристик. Эти характеристики, в отличие от первых, являются скрытыми, так называемыми латентными переменными, поскольку они представляют собой понятия или конструкты, которые не доступны для прямого измерения. Однако они могут быть установлены путем факторизации корреляционных связей между наблюдаемыми чертами и выделением факторов, которые (при условии хорошей структуры) можно интерпретировать как статистическое выражение искомой латентной переменной. В этом случае при проведении измерения мы имеем ряд переменных (показателей) в соответствии с которыми оцениваем характеристики поведения человека или, например, его внешности (в зависимости от целей эксперимента). И в итоге, перед обработкой данных у нас есть некоторый список характеристик и набор оценок по ним.

Психологические задачи факторного анализа. Например, психолог оценивает случайную выборку студентов по следующим параметрам: V1 – вес тела (в кг.) V2 – количество посещений лекций и семинарских занятий по предмету V3 – длина ноги (в см.) V4 – количество прочитанных книг по предмету V5 – длина руки (в см.) V6 – экзаменационная оценка по предмету (V – от английского слова variable – переменная) Данные по каждому испытуемому представляют собой вектор оценок того или иного параметра, так как мы оцениваем не одного испытуемого, а какую-то совокупность. При анализе этих признаков можно предположить, что переменные V1, V3, и V5 будут связаны между собой, так как чем больше человек, тем больше он весит и тем длиннее его конечности. Это означает, что между этими переменными должны получиться статистически значимые коэффициенты корреляции, поскольку эти три переменные измеряют одно общее свойство индивидуумов – их размеры. Так же предположительно будет существовать высокая корреляция между V2, V4 и V6, поскольку посещение лекций и самостоятельные занятия будут способствовать получению более высоких оценок по получаемому предмету.

Психологические задачи факторного анализа. Во-вторых, факторный анализ активно применяется при проведении психосемантических исследований. В этом случае в качестве основной исследовательской задачи выступает выявление особенностей категориальной структуры сознания испытуемых. При этом основная идея исследования остается такой же – выделяемые факторы отражают глубинные процессы (латентные, не наблюдаемые, не измеряемые), являющиеся причиной корреляций первичных (наблюдаемых, измеряемых) переменных. Другими словами, при проведении исследования испытуемым предлагается оценить объекты шкалирования с помощью явных характеристик (конструктов), на основе которых методами факторного анализа выявляются более обобщенные глубинные переменные, с помощью которых испытуемые описывают для себя реальность. При этом психосемантическое исследование ориентировано не только на выбор шкал (переменных), но и самих наблюдений, роль которых играют объекты шкалирования, каждый из которых несет самостоятельную семантическую нагрузку и используется при интерпретации самих результатов. В данном случае, изначально данные представлены в виде матрицы, строками которой являются шкалы (переменные), а столбцами – объекты шкалирования.

Основные понятия факторного анализа. Фактор - это искусственный статистический показатель, возникающий в результате специальных преобразований таблицы коэффициентов корреляции между изучаемыми психологическими признаками, или матрицы интеркорреляций [Ермолаев О.Ю., 2002, С. 275]. Факторные нагрузки – коэффициенты корреляции данного фактора со всеми показателями, использованными в исследовании. Другими словами факторные нагрузки показывают, насколько связаны изучаемые переменные с каждым выделенным фактором – меру, силу этой связи. Ограничения факторного анализа. Следует отметить, что факторный анализ часто подвергают определенным претензиям к точности и достоверности получаемых с его применением результатов. В частности О.В. Митина и И.Б. Михайловская приводят следующие проблемы, связанные с использованием метода факторного анализа (метода главных компонент). Во-первых, отсутствие формальных критериев, которые позволяли бы проверить правильность найденного решения. Во-вторых, после выделения факторов возникает бесконечное множество вариантов вращения, базирующихся на тех же исходных данных, но дающих разные решения (факторная структура определяется несколько иным способом) [Митина О.В., Михайловская И.Б., 2001, С.18-20]. Эти же авторы приводят возможные пути решения этих проблем. В частности, считается, что результат всех процедур можно назвать «хорошим», если выделенные факторные структуры с содержательной точки зрения «имеют смысл». И окончательный выбор между возможными альтернативами внутри бесконечного множества математически равнозначных решений зависит от содержательного осмысления результатов интерпретации [там же].

Основные понятия факторного анализа. В процессе обработки данных необходимо понять, что является особенностями реально присущими категориальной структуре сознания испытуемых (фактами), а что выступает в роли артефактов – результаты обработки данных, причиной появления которых выступают не особенности организации категориальной структуры сознания испытуемых, а влияние особенностей используемого способа счета, и разделить их. Для того, чтобы избежать влияния способа счета данных на получаемые результаты, в ходе обработки данных рекомендуется использовать несколько вариантов факторизации данных. Далее проводить сравнительный анализ полученных факторных структур, ориентируясь на те, которые устойчиво выделяются в каждом из решений. В данном случае, можно утверждать, что полученные факторы будут являться фактами самой категориальной структуры испытуемых, а не артефактами, сопряженными с особенностями метода обработки данных.

Обработка данных методом факторного анализа. Факторный анализ включает в себя следующие этапы : 1. Подготовка исходной матрицы 2. Факторизация данных 3. Вращение факторов 4. Извлечение результатов факторного анализа. 5. Интерпретация полученных данных 1. Подготовка матрицы исходных данных для обработки. Перед проведением факторного анализа необходимо подготовить собранные данные к обработке. При проведении психосемантического исследования, его результаты, как правило, выступают в виде индивидуальных матриц ответов испытуемых, по отношению к которым проводятся две процедуры: 1) получение общей матрицы данных; 2) транспонирование матрицы данных. Получение общей матрицы данных. При использовании психосемантических методов исследования часто в качестве основной исследовательской задачи выступает выявление закономерностей организации категориальной структуры обыденного сознания для всей выборки респондентов в целом, а не по отдельным индивидам. В этом случае возникает необходимость рассматривать всю совокупность данных, полученных на группе индивидов. Сведение данных, полученных на отдельных индивидах, в общую матрицу может быть осуществлено тремя основными способами:

Получение общей матрицы данны 1. Сжатие куба данных. Групповые данные рассматриваются как куб данных (индивидуальная двухмерная матрица, умноженная на количество респондентов), который для последующей обработки должен быть сжат в квадрат. В этом случае проводится поэлементное суммирование слоев исходной матрицы. На рисунке показано, как проводится суммирование первых элементов исходных матриц в Excel. Аналогично суммируются остальные элементы матриц. Размер суммированной матрицы в этом случае будет равен размеру исходных матриц испытуемых. То есть, если исходная матрица одного испытуемого содержала m столбцов и n строк, то суммированная матрица будет содержать такое же количество столбцов и строк.

Получение общей матрицы данны 2. Метод «растягивания в вереницу». В этом случае исходные матрицы составляются одна за другой («в затылок друг другу»). В этом случае матрицы копируются на отдельный лист Excel одна за другой. Если исходная матрица одного испытуемого содержала m столбцов и n строк, и в выборке было А респондентов, то суммированная матрица будет содержать m столбцов и Ахn строк (количество респондентов помноженное на количество строк в исходной матрице). Внимание! Если вы планируете факторизовать данные, полученные методом семантического дифференциала, по дескрипторам, то в общую матрицу следует составлять уже транспонированные (см. далее п. транспонирование матриц) индивидуальные матрицы испытуемых (в которых дескрипторы – столбцы, объекты шкалирования – строки). В этом случае размер вашей общей матрицы будет равен: по числу столбцов – количеству дескрипторов в матрице, по числу строк – количеству объектов шкалирования помноженному на количество испытуемых в выборке. 3. Суммирование матриц интеркорреляций. Данный метод обобщения групповых данных может быть применен в том случае, если вы собирали исходные данные методом репертуарных решеток Келли. В этом случае мы сталкиваемся с ситуацией, когда список объектов шкалирования (оценивания) для всех респондентов будет один, а списки дескрипторов (конструктов) будут индивидуальны для каждого испытуемого. В этом случае для каждого испытуемого исходные данные рассчитываются в матрицу интеркорреляций с использованием разных видов метрик – коэффициента корреляции Пирсона, евклидова расстояния, Сити-блок метрики и т.д. (см. раздел Метрики). Выбор метрики определяется исследовательской задачей. Интрекорреляция данных рассчитывается в данном случае по объектам шкалирования (оценивания), то есть по той составляющей, которая является единой для всех испытуемых. Далее осуществляется поэлементное суммирование индивидуальных матриц интеркорреляций аналогично сжатию куба данных. Как правило, этот метод используется редко, так как для обработки данных, полученных методом репертуарных решеток Келли, чаще всего используется кластерный анализ.

Транспонирование матриц данных

Транспонирование матриц данных Сама матрица представляет собой результат оценок объектов шкалирования по дескрипторам. Факторный анализ осуществляется по переменным (variables), которые описываются столбцами. Эта логика сохранена в пакетах Statistica и SPSS. Если вы планируете проводить факторизацию по дескрипторам, то нужно предварительно провести транспонирование матрицы данных. Эта операция проводится в программе Excel. Для этого вы выделяете матрицу данных, копируете ее, ставите курсор на свободное пространство или другой лист в Excel и выбираете в меню «Правка» функцию «Специальная вставка», в которой выбираете команду «Транспонировать».

Факторизация данных На этом этапе вы обрабатываете методом факторного анализа ваши матрицы данных. Как было сказано выше, факторный анализ проводится на основе матрицы сходства объектов (матрицы интеркорреляций). Вместе с тем, в статистических пакетах Statistica и SPSS можно оперировать матрицей исходных (сырых) данных, так как программа автоматически пересчитает исходную матрицу в матрицу интеркорреляций. Внимание! Если ваша исходная матрица будет содержать столбцы, полностью состоящие из одинаковых значений (например, одни нули, или одни единицы), то матрица корреляций рассчитываться не будет. Программа будет сообщать вам, что у вас нет различий в этом столбце. Вам следует перепроверить данные. После того как вы скопировали вашу матрицу исходных данных в программу (Statistica), вы выбираете в меню Statistics строку Multivariate Exploratory Techniques команду Factor Analysis.

Факторизация данных Далее вы выбираете те переменные (variables), которые будут подвергаться анализу. Как правило, факторизуются все переменные (all variables). Далее программа запрашивает у вас какое количество факторов должно быть получено, и каким методом нужно проводить факторизацию. Обычно в психосемантических исследованиях используется метод основных компонент (principal components). Он же выставляется в программе по умолчанию.

Определение числа факторов Определение числа факторов, используемых для последующего анализа данных, может быть проведено различными методами. Три из них описаны ниже. Определение числа вкладов ряда первых m факторов в общую дисперсию. В работе О.Ю. Ермолаева рекомендуется рассматривать те первые факторы, сумма вкладов которых в общую дисперсию составляет 90% или 95% [Ермолаев О.Ю., 2002, С. 284]. Это достаточно жесткое требование, которое может привести к тому, что в факторной структуре окажется слишком много мелких факторов, плохо поддающихся интерпретации. Можно снизить жесткость этого требования – рассматривать первые n-факторов, сумма вкладов которых в общую дисперсию составляет 75%. Сумма вкладов факторов в пакете Statistica можно получить, нажав на кнопку Eigenvalues

Определение числа факторов В данном примере для последующего анализа данных можно ограничиться рассмотрением первых двух факторов, так как их общий вклад в дисперсию составляет 81,31 %. 2. Критерий каменистой осыпи. «Критерий каменистой осыпи» является графическим методом, впервые предложенным Кэттелем (Cattell, 1966). Другое название этого метода – анализ «следа». При использовании данного метода рассматривается гистограмма собственных значений, расположенных по порядку убывания номеров факторов. Как указывают О.В. Митина и И.Б. Михайловская, «как правило, на графике виден отчетливый излом между крутым наклоном первых факторов и постепенным убыванием остальных». Сама процедура определения факторов заключается в поиске точки на графике, где линия меняет крутизну и приобретает почти горизонтальное положение [Митина О.В., Михайловская И.Б., 2001, С. 94-95]. Так, на рисунке на следующем слайде. отчетливо виден излом на точке, обозначающей третий фактор. В таком случае для интерпретации будет оптимальным выбрать три фактора.

Определение числа факторов

Вращение факторов После того, как определено количество факторов, рассматриваемых для последующего анализа следующая процедура – вращение факторов. Вращение (ротация) факторов изменяет положение факторов по отношению к переменным таким образом, что полученное решение легко интерпретировать. Факторы интерпретируют, наблюдая, какие переменные имеют большие и/или нулевые нагрузки по ним. Решения, которые не подчиняются интерпретации, - это те решения, в которых большое число переменных имеет нагрузки среднего уровня (порядка 0,3). Вращение факторов перемещает факторы относительно переменных таким образом, что каждый фактор начинает обладать несколькими существенными нагрузками и несколькими нагрузками равными нулю [Ермолаев О.Ю., 2002, С. 285]. Иначе говоря, процедура вращения позволяет сделать нам факторы более пригодными для интепретации. Выделяют несколько видов вращения. Более подробно о разных видах вращения можно прочитать в соответствующей литературе [Ермолаев, 2002, С. 285-287; Митина О.В., Михайловская И.Б., 2001 и т.д.]. В психологии традиционно используется метод Варимакс-вращения (Varimax). Для вращения полученных данных вы выбираете в строке Factor rotation вид вращения Varimax normalized.

Вращение факторов

Результаты анализа Далее мы можем извлечь результаты факторного анализа из программы. Как правило, нас интересуют три вида результатов: 1. Факторные нагрузки переменных. Так как факторный анализ ориентирован, прежде всего, на упрощение структуры данных, то этот результат позволяет понять, какой вклад вносит каждая переменная (variables) в фактор. В психосемантических исследованиях в виде переменных чаще всего выступают дескрипторы. В пакете Statistica факторные нагрузки данных можно посмотреть, нажав на кнопку Summary: Factor Loading в меню результатов. Данные выглядят как таблица, в которой каждой переменной (variables) соответствует ее факторная нагрузка в факторе. Эти данные копируются в Excel и далее используются для интерпретации полученных факторов (см. п. интерпретация данных). На рисунке показан фрагмент окна результатов – факторные нагрузки.

Результаты анализа 2. Распределение случаев по полюсам фактора. Эти данные показывают, как распределяются случаи (cases) по полюсам фактора. В психосемантическом исследовании в роли случаев выступают объекты шкалирования. В пакете Statistica распределение случаев по фактору можно посмотреть, нажав на кнопку Factor Scores в меню результатов. Данные выглядят как таблица, в которой обозначены координаты каждого случая (cases) в пространство фактора. Эти данные также могут быть использованы для дополнительной интерпретации полученных факторов. Мы можем посмотреть, каким полюсам факторов соответствуют те или иные объекты шкалирования.

Результаты анализа 3. Вес факторов в общей дисперсии (% Total variance). Распределение факторов в общей дисперсии нам необходимо, во-первых, для определения количества рассматриваемых факторов. Во-вторых, для понимания того, какой объем общих данных мы можем объяснить полученными нами факторами. Посмотреть вес факторов в общей дисперсии в пакете Statistica можно, нажав на кнопку Eigenvalues.

Результаты анализа 3. Интерпретация данных, полученных методом факторного анализа Интерпретация данных, полученных методом факторного анализа, выступает своего рода искусством, призванным проявить исследовательскую культуру интерпретатора. Это наиболее интересный, хотя и трудоемкий этап исследования. Основные принципы интерпретации данных: 1. Факторный анализ направлен на упрощение структуры упрощение структуры рассматриваемых данных (редукция данных), а также выявление латентных переменных на основе наблюдаемых характеристик. Так, с помощью классического семантического дифференциала Г. Осгуда было выявлено три основных характеристики, с помощью которых люди оценивают окружающий мир – «Сила», «Активность» и «Оценка». При интерпретации мы ориентируемся на то, что из множества шкал, по которым оценивались объекты, будут выделены факторы, образованные шкалами наиболее значимо коррелирующими между собой. 2. При оценке испытуемыми тех или иных объектов разные шкалы имеют разную значимость (когнитивную приоритетность). Аналогом такой значимости в факторном анализе выступает вес фактора в общей дисперсии (% Total variance). Чем больше вес фактора в общей дисперсии, тем большую часть данных он объясняет, тем более значимым он является при оценке испытуемым части реальности, относительно которой изучались его представления. Первый фактор в факторной структуре является наиболее значимым, он же имеет наиболее высокий вес в общей дисперсии (% Total variance). Далее степень значимости каждого из факторов последовательно снижается. Математически это означает, что первый фактор описывает наибольшую часть от объема всех данных (равную, соответственно, его весу в общей дисперсии). Психологически же это говорит о том, фактор с набольшим факторным весом является наиболее значимым для испытуемых при оценке и описании соответствующих аспектов реальности.

Результаты анализа 3. Содержательно полученные факторы интерпретируются исходя из того, какие именно переменные (в психосемантике – дескрипторы, конструкты) максимально коррелируют с данным фактором. Для этого используется факторные нагрузки переменных, которые фактически являются коэффициентами корреляции переменных с фактором. Каждая из переменных имеет разное значение для описания этого фактора. Наиболее значимы для описания фактора те переменные, факторная нагрузка которых близка к 1 (-1). Переменные, факторная нагрузка которых находится в пределах от 0,4 до -0,4, в интерпретации фактора не рассматриваются, так как практически не связаны с ним. На основе содержательного анализа тех переменных, для которых наиболее высоки факторные нагрузки по данном фактору, делается вывод о том, как может быть обозначен данный фактор. Другими словами, делается интерпретация и дается название фактору на основе дескрипторов, входящих в этот фактор. Примечание. Если в факторе выделяется слишком много переменных, факторная нагрузка которых велика При этом часто возникает вопрос, а какую часть переменных следует оставить для интерпретации фактора? Оптимальным способом здесь будет руководствоваться наличием скачка между значениями факторных нагрузок дескрипторов. Например, в таблице на следующем слайде видно, что значение факторной нагрузки переменных со второго дескриптора снижается постепенно: "деликатесный" (0,88), "съедобный" (0,88), "насыщенный" (0,85), "экзотический" (0,84). А потом происходит резкий скачок факторной нагрузки от 0,85 до 0,74. Мы можем рассматривать это как скачок, и начиная с дескриптора "заморский" остальные дескрипторы при интерпретации фактора не рассматривать. Но так же мы могли бы убрать из интерпретации дескрипторы, начиная с "пряный" - там тоже есть скачок факторной нагрузки переменных от 0,70 до 0,61.

Результаты анализа

Рекомендованные к использованию в рамках дисциплины статистические компьютерные пакеты Не поленитесь установить эти пакеты, каждый из них имеет свои преимущества и недостатки, уникальные возможности. Подробно будем знакомиться на лабораторных работах. Работают под Windows. Primer of Biostatistics. Легчайшая, portable, содержит большую часть методов (кроме многомерных), а также расчет размеров выборки, мощности, то есть планирование эксперимента https://yadi.sk/d/9jixxsf2uzxsM StatMed. Легчайшая, portable, содержит базовые методы в основном для количественных данных, четкий алгоритм принятия решений – какие критерии применять – параметрические или непараметрические https://yadi.sk/d/qsIQJ4IGuzyVa MedStat. Легчайшая, portable, содержит базовые методы для количественных и качественных (органичения демо-версии на множественные сравнения), По сути – расширенный вариант StatMed. Для большинства случаев – наиболее годный и пошаговый инструмент. https://yadi.sk/d/vXnsrGNWrngzk

Рекомендованные к использованию в рамках дисциплины статистические компьютерные пакеты Biostat. Более сложный инструмент по сравнению с представленными выше, в то же время прекрасно русифицирован и позволяет решать большинство задач начиная от планирования эксперимента, за исключением некоторых многомерных методов, например факторного и кластерного анализа https://yadi.sk/d/kGEWv92Wv22SX StatSoft Statistica. Версия 10 – довольно новая, много улучшений. Непросто установить, не сразу поддается пониманию, особенно самостоятельному. В большинстве случаев – эталонный инструмент. Есть прекрасные обучающие материалы в Интернете https://yadi.sk/d/oZD1Un_hv22xj SPSS Statistics 21 версия. Плюс модуль AMOS. В программе есть всё и даже больше. С другой стороны, не всем (мне в том числе) нравится интерфейс. Преимущества – прекрасная русификация, много обучающих материалов в Интернете. https://yadi.sk/d/FyntqfDMv23Gp Кстати, Microsoft Excel и его аналоги (другие табличные процессоры) никто не отменял. Они содержат существенные возможности статистической обработки данных