🗊Презентация Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. (Лекция 10)

Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. Несобственные интегралы. Лекция 10

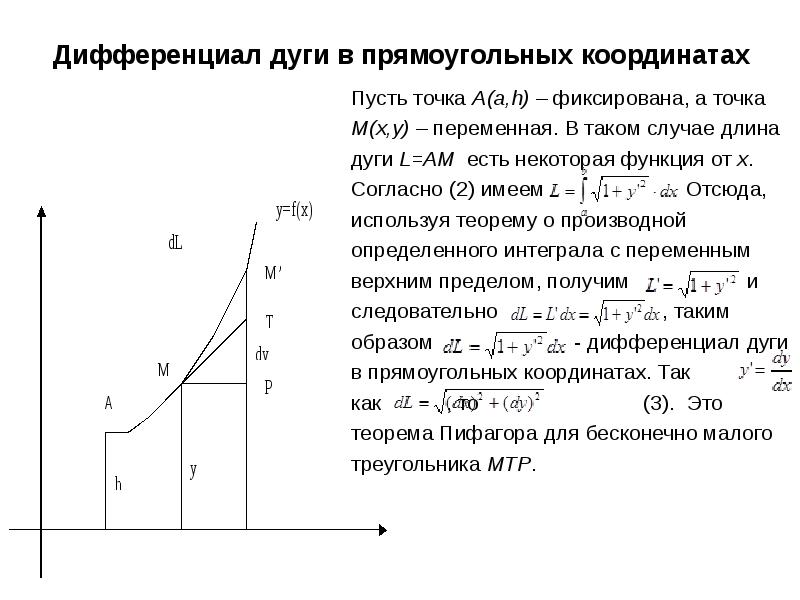
О1 О1 Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена ее стремится к нулю. О2 Кривая называется гладкой, если она непрерывна и в каждой точке имеет касательную, непрерывно меняющую свое положение от точки к точке. Кривая задана уравнением (1) f’(x) – непрерывна на отрезке [a,b]. Теорема Всякая гладкая кривая (1) имеет определенную конечную длину дуги.

Док-во: Док-во: Впишем в данную гладкую кривую (1) ломаную линию Проектируя звенья ломаной на ось ОХ, получим разбиение отрезка [a,b] на систему отрезков . Пусть - приращение функции y=f(x) на отрезке [a,b]. По теореме Пифагора имеем . Применяя теорему Лагранжа о конечном приращении функции, получим , где - некоторая промежуточная точка отрезка . Отсюда . Длина всей ломаной линии (то есть ее периметр) равна . Для нахождения длины L кривой (1) в последнем выражении переходим к пределу при и . Таким образом Получаем предел интегральной суммы для непрерывной функции Поэтому или (2), где y’=f’(x)

Дифференциал дуги в прямоугольных координатах Пусть точка A(a,h) – фиксирована, а точка M(x,y) – переменная. В таком случае длина дуги L=AM есть некоторая функция от х. Согласно (2) имеем Отсюда, используя теорему о производной определенного интеграла с переменным верхним пределом, получим и следовательно , таким образом - дифференциал дуги в прямоугольных координатах. Так как , то (3). Это теорема Пифагора для бесконечно малого треугольника MTP.

Пример Пример Вычислить длину дуги отрезка цепной линии. Так называется линия, форму которой принимает тяжелая нить, закрепленная в двух точках. Уравнение линии (4), где а – параметр цепной линии, а>0. Или проще (4’) – гиперболический косинус. b – абсцисса точки В; h – ордината точки В. Дифференцируя уравнение (4’) получаем . Далее . Тогда . Согласно формулы (2), имеем

Нахождение длины дуги кривой, заданной параметрическими уравнениями Пусть L – длина дуги кривой , , - непрерывно дифференцируемые функции на заданном отрезке. Формула (3) для дифференциала дуги справедлива и в этом случае dx=x’dt; dy=y’dt. Имеем Интегрируя последнее выражение в пределах от до t=T получим длину дуги (5) Пример Найти длину дуги окружности, заданной параметрическими уравнениями от t=0 до t=T Решение Здесь dx=-asintdt; dy=acostdt. Поэтому и, следовательно

Пример Пример Найти длину дуги астроиды Запишем уравнение астроиды в следующем виде Замена . Получаем параметрические ура-ния астроид (6). Кривая (6) симметрична, поэтому находим при изменении t от 0 до . Получаем . Отсюда . Интегрирую в пределах от t=0 до , получим

Длина дуги в полярных координатах Выведем сначала формулу для дифференциала dL дуги в полярных координатах на основании формулы (3) , где x,y – прямоугольные декартовы координаты точки дуги. Формулы перехода: Отсюда , следовательно или (1), где Задача Найти длину дуги L непрерывно дифференцируемой кривой между точками и , где - полярные координаты. Интегрируя равенство (1) в пределах от до получаем длину дуги в полярных координатах , где - производная

Пример Пример Вычислить полную длину дуги кардиоиды Решение Имеем , тогда , отсюда

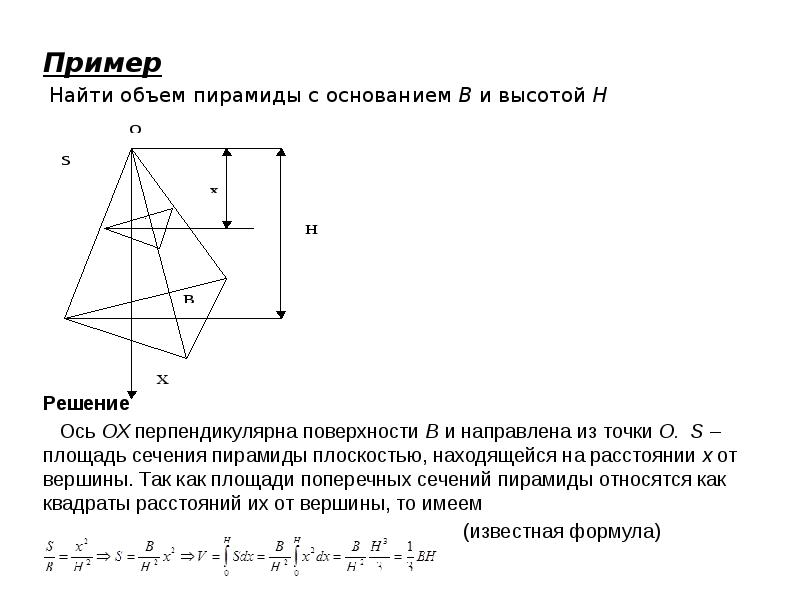
Вычисление объема тела по известным поперечным сечениям Задача Зная закон изменения площади поперечного сечения тела, найти объем этого тела. Пусть ОХ некоторое выбранное направление и S(x) – площадь поперечного сечения плоскостью перпендикулярной оси ОХ в точке с абсциссой х. Функцию S(x) будем предполагать известной и непрерывно меняющейся при изменении х. Проектируя тело на ось ОХ, получим некоторый отрезок [a,b], дающий линейные размеры тела в направлении оси ОХ. Разобьем данное тело на элементарные слои плоскостями, перпендикулярными оси ОХ. Точки пересечения этих плоскостей с осью ОХ соответственно .

Каждый элементарный слой, ограниченный плоскостями, пересекающимися в точках заменяем цилиндром с высотой и площадью основания . Объем данного цилиндра выражается формулой . Составим сумму всех таких Каждый элементарный слой, ограниченный плоскостями, пересекающимися в точках заменяем цилиндром с высотой и площадью основания . Объем данного цилиндра выражается формулой . Составим сумму всех таких произведений . Эта сумма является интегральной для данной функции S=S(x) на отрезке [a,b]. Она выражает объем ступенчатого тела, состоящего их элементарных цилиндров и приближенно заменяющего данное тело. Объемом тела называют предел объема указанного ступенчатого тела, приближенно заменяющего данное тело, при - длина наибольшего из элементарных отрезков . По определению с другой стороны . Из двух последних равенств получаем формулу вычисления объема тела по заданным поперечным сечениям.   (1)

Пример Пример Найти объем пирамиды с основанием В и высотой Н Решение Ось ОХ перпендикулярна поверхности В и направлена из точки О. S – площадь сечения пирамиды плоскостью, находящейся на расстоянии х от вершины. Так как площади поперечных сечений пирамиды относятся как квадраты расстояний их от вершины, то имеем (известная формула)

Объем тела вращения Задача Найти объем тела, образованного вращением вокруг оси ОХ криволинейной трапеции aABb, ограниченной данной непрерывной линией , отрезком оси ОХ и двумя вертикалями x=a, x=b Эта задача – частный случай задачи, рассмотренной выше. Здесь площадь переменного поперечного сечения S=S(x), соответствующего абсциссе х, есть круг радиуса у, поэтому и формула (1) примет вид (2)

Задача Задача Найти объем тела, образованного вращением вокруг оси ОУ криволинейной трапеции cCDd, ограниченной данной непрерывной линией , отрезком оси ОУ и двумя горизонталями y=c, y=d По аналогии с формулой (2) (3) Примеры 1. Вычислить объем тела, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями Решение Пределы интегрирования a=1,b=6, функция 2. Вычислить объем тела, полученного в результате вращения вокруг оси ОХ криволинейной трапеции, ограниченной линией , осями координат и прямой х=1  Решение Пределы интегрирования a=0,b=1, функция

3. Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг оси ОХ (и ОУ) 3. Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг оси ОХ (и ОУ) Так как эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси ОХ площади ОАВ, равной ¼ площади эллипса, и полученный результат удвоить. Окончательно и соответственно

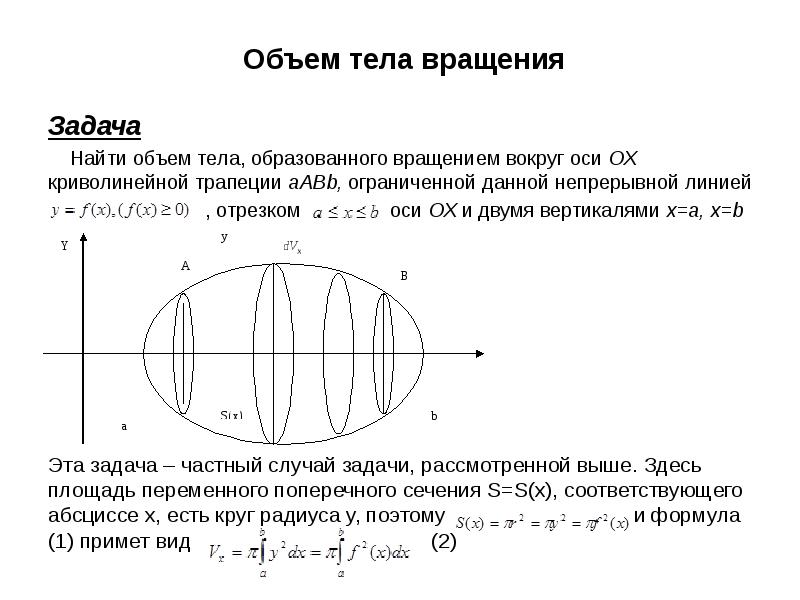
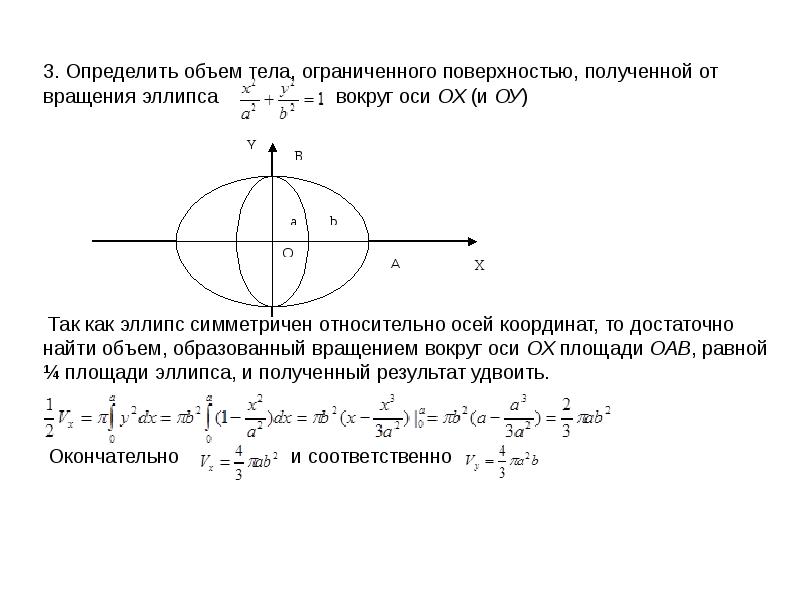
Несобственные интегралы При определении интеграла (1) предполагалось, что: 1) Отрезок интегрирования [a,b] – конечен; 2) f(x) определена и непрерывна на отрезке [a,b]. Такой определенный интеграл называется собственным (название опускается). Если нарушается по крайней мере одно из двух условий 1) или 2), то (1) называется несобственным определенным интегралом. Рассмотрим смысл этого понятия для двух простейших случаев Пусть f(x) непрерывна при . Тогда по определению полагают (2) Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), называется сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.

Геометрическая интерпретация Геометрическая интерпретация Геометрически для неотрицательной на функции f(x) несобственный интеграл (2) представляет собой площадь криволинейной фигуры, ограниченной данной линией y=f(x), осью ОХ и вертикалью х=а. Пусть F(x) первообразная для f(x). На основании формулы (2) имеем . Если ввести условное обозначение , то получим для сходящегося несобственного интеграла с бесконечным верхним пределом обобщенную формулы Ньютона-Лейбница (3), где F’(x)=f(x). Примеры 1) 2) Установить, при каких значениях интеграл сходится и при каких расходится

Решение Так как при , то Решение Так как при , то . Следовательно , можно сделать следующие выводы: Если , то - интеграл сходится; Если , то - интеграл расходится; Если , то - интеграл расходится; 3.Вычислить (второй интеграл равен (см. Пример 1)). Вычислим следовательно Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, оценить его значение. Для этого могут быть полезны следующие теоремы. Теорема 1 Если для любого х выполняется неравенство и если сходится, то также сходится , при этом

4. Исследовать, сходится ли интеграл 4. Исследовать, сходится ли интеграл Решение При сходится и его значение меньше или равно 1. Теорема 2 Если для любого х выполняется неравенство и если расходится, то также расходится. 5. Исследовать, сходится ли интеграл Решение При следовательно расходится и данный интеграл. Для функции меняющий знак в бесконечном интервале, имеет место следующая теорема. Теорема 3 Если интеграл сходится, то сходится и интеграл . В этом случае последний интеграл называется абсолютно сходящимся. 6. Исследовать, сходится ли интеграл Решение При следовательно сходится и данный интеграл.

II. Интеграл от разрывной функции Пусть функция f(x) непрерывна при и имеет точку разрыва при x=b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой. Если предел, стоящий справа существует, то интеграл называется несобственным сходящимся, иначе расходящимся. Если f(x) имеет разрыв в левом конце отрезка [a,b], то есть при x=a, то по определению Если f(x) имеет разрыв в некоторой точке , то полагают , если оба несобственных интеграла, стоящих в правой части равенства существуют. Пример 1 Вычислить Решение

Пример 2 Вычислить Пример 2 Вычислить Решение Так как внутри отрезка интегрирования существует точка x=0, где подынтегральная функция разрывна, то интеграл нужно представить как сумму двух слагаемых: Вычислим данные интегралы . Следовательно, на участке [-1;0] интеграл расходится . Следовательно, на участке [0;1] интеграл расходится. Таким образом, данный интеграл расходится на всем отрезке [-1;1]. Отметим, что, если бы стали вычислять интеграл, не учитывая разрыв подынтегральной функции в точке x=0, то получили бы неверный результат.

Замечание Если f(x), определенная на [a,b], имеет внутри этого интеграла конечное число точек разрыва , то интеграл от f(x) на [a,b] определяется следующим образом: Замечание Если f(x), определенная на [a,b], имеет внутри этого интеграла конечное число точек разрыва , то интеграл от f(x) на [a,b] определяется следующим образом: , если каждый интеграл в правой части равенства сходится. Если же, хотя бы один из этих интегралов расходится, то расходится и исходный интеграл. Имеют место теоремы Теорема 1 Если на [a,b] функции разрывны в точке b, причем во всех точках [a,b] выполняется неравенство и если сходится, то также сходится. Теорема 2 Если на [a,b] функции разрывны в точке b, причем во всех точках [a,b] выполняется неравенство и если расходится, то также расходится. Теорема 3 Если на [a,b] функции знакопеременна и разрывна в точке b и если сходится, то также сходится. В качестве функций, с которыми удобно сравнивать функции, стоящие под знаком интеграла, часто берут . Легко проверить, что сходится при и расходится при

Пример 3 Сходится ли интеграл Пример 3 Сходится ли интеграл Решение Подынтегральная функция разрывна в точке x=0. Сравнивая ее с функцией имеем . Интеграл существует. Следовательно, интеграл от меньшей функции также существует.